7.3: Common Discrete Fourier Series
- Page ID
- 22881
Introduction
Once one has obtained a solid understanding of the fundamentals of Fourier series analysis and the General Derivation of the Fourier Coefficients, it is useful to have an understanding of the common signals used in Fourier Series Signal Approximation.
Deriving the Coefficients
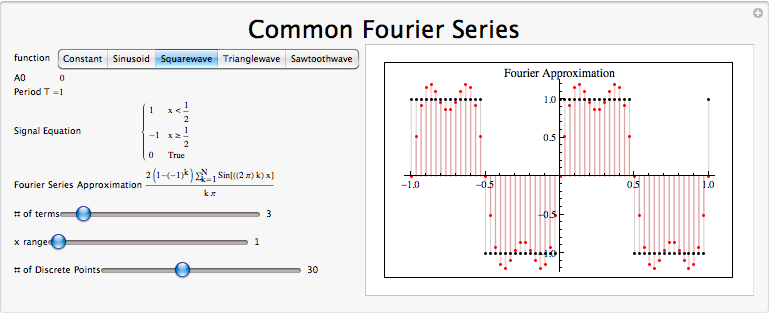
Consider a square wave \(f(x)\) of length 1. Over the range [0,1), this can be written as
\[x(t)=\left\{\begin{array}{rl}
1 & t \leq \frac{1}{2} \\
-1 & t>\frac{1}{2}
\end{array}\right. \nonumber \]

Real Even SignalsGiven that the square wave is a real and even signal,
- \(f(t)=f(−t)\) EVEN
- \(f(t)=f^*(t)\) REAL
therefore,
- \(c_n=c_{−n}\) EVEN
- \(c_n=c_n^*\) REAL
Deriving the Coefficients for other signals
The Square wave is the standard example, but other important signals are also useful to analyze, and these are included here.
Constant Waveform
This signal is relatively self-explanatory: the time-varying portion of the Fourier Coefficient is taken out, and we are left simply with a constant function over all time.
\[x(t)=1 \nonumber \]

Figure \(\PageIndex{2}\)
Sinusoid Waveform
With this signal, only a specific frequency of time-varying Coefficient is chosen (given that the Fourier Series equation includes a sine wave, this is intuitive), and all others are filtered out, and this single time-varying coefficient will exactly match the desired signal.
\[x(t)=\cos (2 \pi t) \nonumber \]
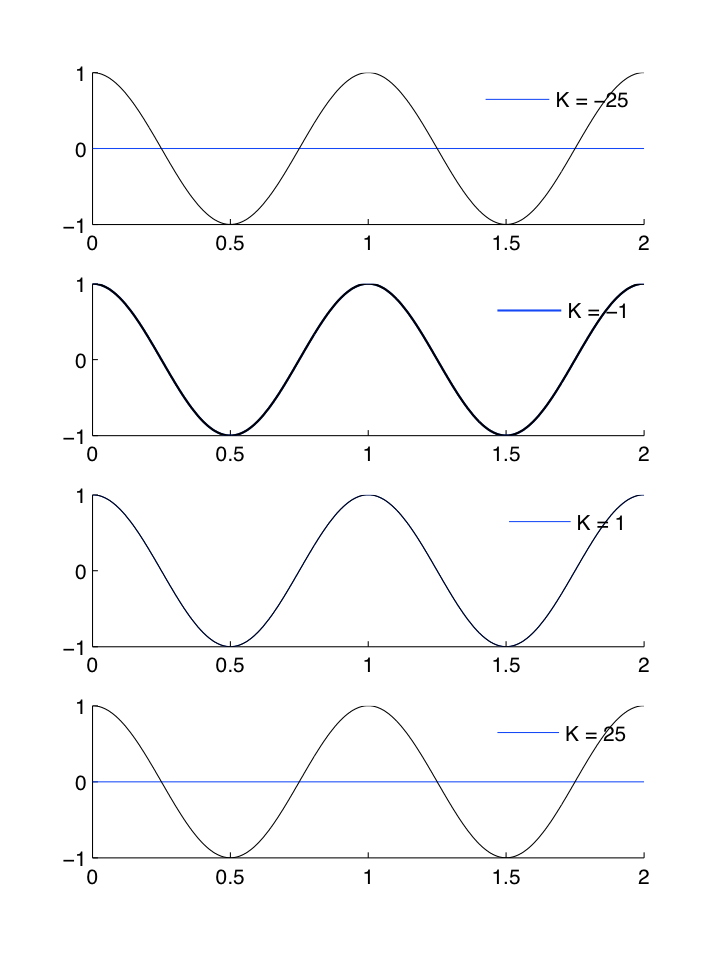
Figure \(\PageIndex{3}\)
Triangle Waveform
\[x(t)=\left\{\begin{array}{rl}
t & t \leq 1 / 2 \\
1-t & t>1 / 2
\end{array}\right. \nonumber \]
This is a more complex form of signal approximation to the square wave. Because of the Symmetry Properties of the Fourier Series, the triangle wave is a real and odd signal, as opposed to the real and even square wave signal. This means that
- \(f(t)=−f(−t)\) ODD
- \(f(t)=f^*(t)\) REAL
therefore,
- \(c_n=−c_{−n}\)
- \(c_n=−c_n^*\) IMAGINARY
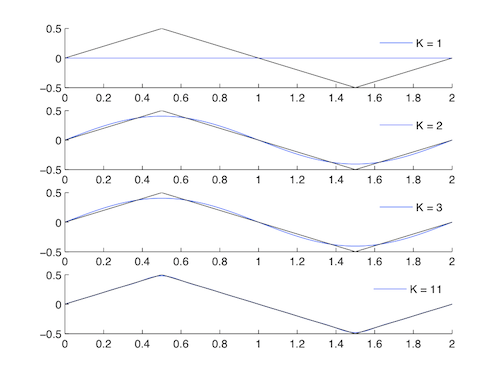
Figure \(\PageIndex{4}\)
Sawtooth Waveform
\[x(t) = t/2 \nonumber \]
Because of the Symmetry Properties of the Fourier Series, the sawtooth wave can be defined as a real and odd signal, as opposed to the real and even square wave signal. This has important implications for the Fourier Coefficients.
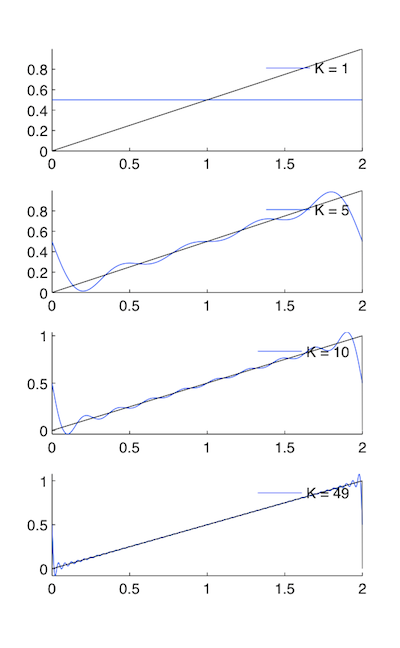
Figure \(\PageIndex{5}\)
Conclusion
To summarize, a great deal of variety exists among the common Fourier Transforms. A summary table is provided here with the essential information.
| Description | Time Domain Signal for \(n \in \mathbb{Z}[0, N-1]\) | Frequency Domain Signal \(k \in \mathbb{Z}[0, N-1]\) |
| Constant Function | 1 | \(\delta(k)\) |
| Unit Impulse | \(\delta(n)\) | \(\frac{1}{N}\) |
| Complex Exponential | \(e^{j 2 \pi m n / N}\) | \(\delta\left((k-m)_{N}\right)\) |
| Sinusoid Waveform | \(\cos (j 2 \pi m n / N)\) | \(\frac{1}{2}\left(\delta\left((k-m)_{N}\right)+\delta\left((k+m)_{N}\right)\right)\) |
| Box Waveform \((M < N/2)\) | \(\delta(n)+\sum_{m=1}^{M} \delta\left((n-m)_{N}\right)+\delta\left((n+m)_{N}\right)\) | \(\frac{\sin ((2 M+1) k \pi / N)}{N \sin (k \pi / N)}\) |
| Dsinc Waveform \((M<N/2)\) | \(\frac{\sin ((2 M+1) n \pi / N)}{\sin (n \pi / N)}\) | \(\delta(k)+\sum_{m=1}^{M} \delta\left((k-m)_{N}\right)+\delta((k+m)_N)\) |