8.5: Continuous Time Convolution and the CTFT

Last updated
Save as PDF

Page ID: 22890

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Introduction

This module discusses convolution of continuous signals in the time and frequency domains.

Continuous Time Fourier Transform

The CTFT transforms a infinite-length continuous signal in the time domain into an infinite-length continuous signal in the frequency domain.

CTFT

\[\mathcal{F}(\Omega)=\int_{-\infty}^{\infty} f(t) e^{-(j \Omega t)} d t \nonumber \]

Inverse CTFT

\[f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \mathcal{F}(\Omega) e^{j \Omega t} d \Omega \nonumber \]

Convolution Integral

The convolution integral expresses the output of an LTI system based on an input signal, \(x(t)\), and the system's impulse response, \(h(t)\). The convolution integral is expressed as

\[ y(t)=\int_{-\infty}^{\infty} x(\tau) h(t-\tau) d \tau \nonumber \]

Convolution is such an important tool that it is represented by the symbol *, and can be written as

\[y(t)=x(t) * h(t) \nonumber \]

Convolution is commutative. For more information on the characteristics of the convolution integral, read about the Properties of Convolution (Section 3.4).

Demonstration

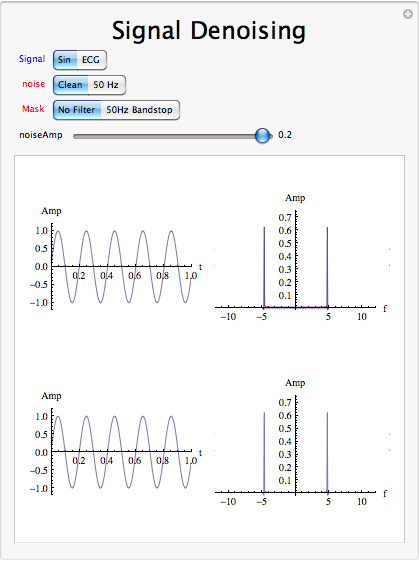
CTFTdenoiseDemo — Figure \(\PageIndex{1}\): Interact (when online) with a Mathematica CDF demonstrating Use of the CTFT in signal denoising. To Download, right-click and save target as .cdf.

Convolution Theorem

Let \(f\) and \(g\) be two functions with convolution \(f*g\). Let \(F\) be the Fourier transform operator. Then

\[F(f * g)=F(f) \cdot F(g) \nonumber \]

\[F(f \cdot g)=\frac{1}{2 \pi} F(f) * F(g) \nonumber \]

By applying the inverse Fourier transform \(F^{−1}\), we can write:

\[f * g=F^{-1}(F(f) \cdot F(g)) \nonumber \]

Conclusion

The Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain (e.g., time domain) corresponds to point-wise multiplication in the other domain (e.g., frequency domain).