4.3: Gutter and Downspout Sizing
- Page ID
- 11937
Once the rain falls on the roof, gutters (i.e., conveyance) are usually needed to direct the rainfall to any treatment, storage, and/or end use. Pipes that are too small will restrict water from flowing through the system fast enough, resulting in overflow or overloading. Pipes that are too large will convey the water easily but could prove cost-restrictive or unsightly. More slope will help evacuate the pipes faster but may be harder to build and less attractive.
There are many ways to size gutters. One of the simplest is the following rule of thumb:
\[\frac{1\;cm^2\;of\;gutter\;cross\;section}{1\;m^2\;of\;roof\;area}\]
Four other methods are:
- If you are using a standard gutter, e.g. “K” style gutters, many online calculators exist.
- If you are using standard pipe, pipe friction tables can be used to find an acceptable amount of pressure (head) loss.
- For full pipes of various materials and sizes, the Darcy-Weisbach method (or easier, the Hazen-Williams method) can be used to find an acceptable amount of head loss.
- For open channel flow, the Manning Equation can be used to find an acceptable amount of head loss.
The four other methods are more accurate than the simple rule of thumb, and some allow for factors such as roof pitch, the strength of local storms, and other shapes besides cylindrical pipe.
Example \(\PageIndex{1}\)
The minimum pipe size needed for a catchment area of 23 \(m^2\) is calculated to be 23 \(cm^2\) using the rule of thumb in Equation 6 as shown below: The needed cross-sectional area of gutter is 23 \(cm^2\). To convert that cross-sectional area to the diameter of the pipe, remember that the formula for the area of a circle (which is the cross-section of a pipe) is the following:
\[Gutter\;cross\;sectional\;area=23\;m^2*\frac{1\;cm^2}{1\;m^2}=23\;cm^2\]
The needed cross-sectional area of gutter is 23 \(cm^2\). To convert that cross-sectional area to the diameter of the pipe, remember that the formula for the area of a circle (which is the cross-section of a pipe) is the following:
\[Area\;of\;a\;Circle=π*r^2\]
Where:
- A = Area
- π ≈ 3.1416
- r = radius, which is half of the diameter (\(\frac{d}{2}\)).
Therefore:
\[Area\;of\;a\;Circle=π*(\frac{d}{2})^2\]
Solving for diameter yields:
\[d=2*\sqrt{\frac{Area\;of\;a\;Circle}{π}}\]
\[d=2*\sqrt{\frac{23\;cm^2}{π}}=5.41\;cm\]
Converting the diameter to inches (which is the common unit of measure for pipe size) yields:
\[5.41\;cm*\frac{1\;in}{2.54\;cm}=2.13\;in\]
Therefore, a pipe diameter of at least 2.13 inches should be used. The most common size that meets that requirement is 2.5-inch pipe.
This rule of thumb works for most situations, but ultimately the sizing depends on the strength of local storms, the pitch of the roof, and the slope of the gutter. In addition to gutter sizing, the gutter slope must be addressed. In order to keep the water flowing through gutters via gravity, a slope is needed to provide pressure from the elevation difference (Figure 4-2).
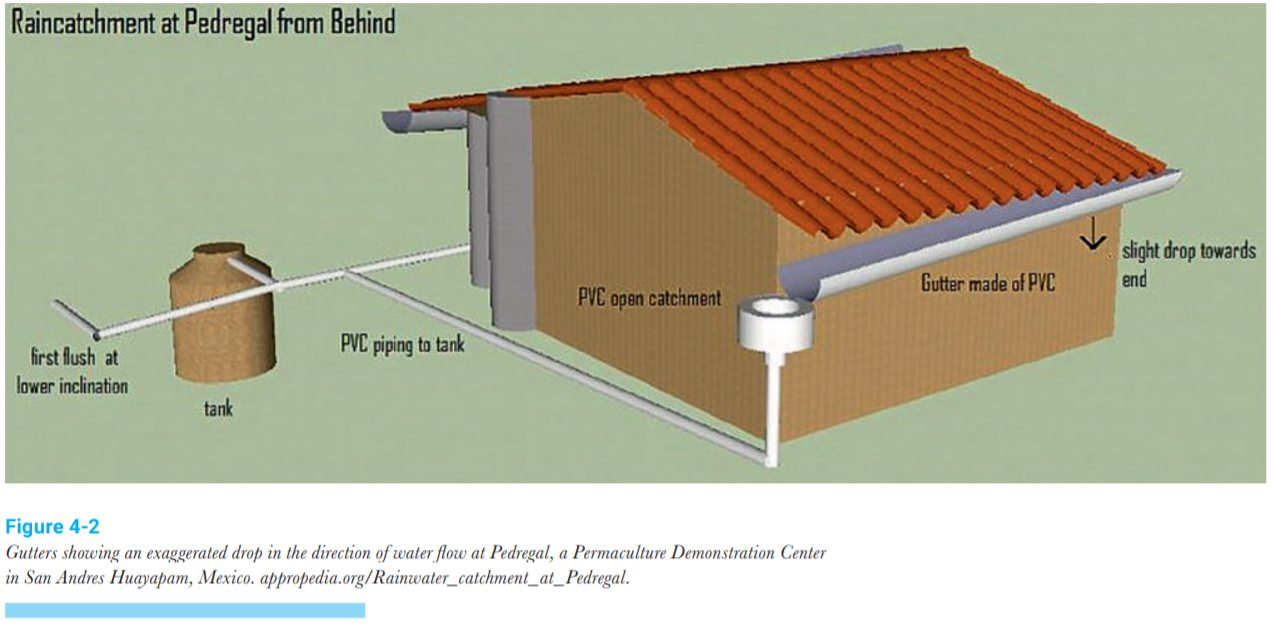
A common ratio for the needed slope is \(\frac{1}{2}\) inch drop for every 10 feet of run, as shown in Equation 8:
\[\frac{\frac{1}{2}\;in\;a\;drop}{10\;feet\;of\;gutter\;rain}\]
Example \(\PageIndex{2}\)
Using the common gutter slope ratio, calculate the drop needed for a 30-foot-long gutter.
Solution
\[drop=30\;ft*\frac{\frac{1}{2}\;in}{10\;feet}=1.5\;in\]
Therefore, one end of the 30-foot gutter should be approximately 1.5 inches above the other to ensure proper flow through the gutters.


