13.3: Six Sigma- What is it and what does it mean?
- Page ID
- 22524
Introduction
Every generation of business strives for a new level of quality. The quality program that is currently in vogue and being widely used and recognized by industry is the Six Sigma program. Six Sigma is a relatively new program, and was only started in 1986. It was first put into implementation at Motorola, but is now in use by most large corporations. Some of these other large companies include GE, Honeywell, and Bank of America. The Six Sigma program is in place to eliminate any abnormalities, failures, or defects that occur within a given process. These are problems that already exist. DFSS (Design for six sigma) starts earlier, to develop or redesign the process itself, so fewer wrinkles show up in the first place, thus systematically preventing downstream errors. Six Sigma is also used in developing new processes. The Six Sigma program strives to achieve six standard deviations between the mean and the closest specification limit on a short term study. Studies run to obtain this goal are short term capability studies, which include common cause or random variation, such as operator control, and long term studies, which include random and special types of variation. Both of these studies are evaluated on a Z-scale. The short term data variability which makes up long term variability tends to cause the mean to shift. This shift of the mean is by 1.5 standard deviations. Most companies are looking on a long term scale, because they would rather have a good/safe product in the long run/for a long time rather than for a short amount of time. Using this idea, the goal for the Six Sigma program is to have fewer than 3.4 failures per one million opportunities when the data is evaluated to include the shifted mean from process variability (6 standard deviations - 1.5 standard deviations = 4.5 standard deviations). The 4.5 vs 6 standard deviations is the same goal, but the 4.5 represents data variation in the long run, which is used in most processes. We will be using the shifted mean scenario for the rest of this article when referring to opportunity goals. This leaves very slight room for error on a process and leads to a very high level of quality in the products.

The often-used six sigma symbol.
To reiterate, the term "Six Sigma" comes from the standard deviation and the Gaussian distribution. 3.4 failures per one million opportunities represents 4.5 standard deviations (sigma) away from the median value, either up or down, under a bell curve. This will be discussed further below along with what the Six Sigma program represents, what mathematically this means, and finally what a Gaussian distribution is. After the basics have been covered we will move onto Statistical Process Control. Statistical Process Control is different ways to analyze the data that you have obtained. Finally, we will relate Six Sigma to process control and explain how you can tell if something is in Six Sigma control or not.
The Six Sigma Program
Six Sigma is defined as a measure of quality that organizations strive to achieve. It is a disciplined, data-driven approach used to eliminate defects in any process – from manufacturing to transactional and from product to service. Six Sigma does not refer to a process operating within 6 or 4.5 standard deviations of the desired state. To achieve Six Sigma, a process must not produce more than 3.4 defects per million opportunities, where a defect is defined as anything outside of the customer specification. One million opportunities, and only 3.4 defects? Sounds like an efficient process. Here is an example that will help demonstrate. Let’s say a surgeon at the top of his field has a 5.51 sigma ranking. Sounds pretty good, right? That means that if he operates on 1,000,000 patients per year he loses 30 of them. When a process is operating at Six Sigma, it is seen that there are essentially zero defects within a process.
In chemical engineering, many different processes require strict, robust control. For example, a reactor may need to be maintained between a specified temperature range to keep the plant safe. However, there is also an optimum temperature at which the reaction will occur. Engineers will want to keep a tight control around this temperature to make the system more efficient, while also closely watching the variable and keeping track of how close it gets to the control limits. Crossing the control limits is not the only problem. In order for a system to be in statistical control as stated by the Six Sigma program, the data points must not frequently approach the same control limit. The Six Sigma program helps engineers monitor processes to keep them within their desirable ranges. Many industries employ the Six Sigma system as well as its hierarchy of positions to champion data-driven problem solving.
Originally invented by Motorola, the Six Sigma system contains belt rankings that represent a person’s achievements utilizing Six Sigma methodologies and associated roles and responsibilities. These rankings are modeled after the martial arts system, as detailed below.
Yellow Belts (YB)
Yellow belt is the first level in the Six Sigma program. To get yellow belt status one must go through a training course in Six Sigma and pass an online certification. Yellow belt team members do not lead projects on their own, but they are usually a core team member with special knowledge on a project. Yellow belts are responsible for:
- The development of process maps to support Six Sigma projects.
- Running smaller process improvement projects using the Plan, Do, Check, Act (PDCA) method
- Being a subject matter expert on the Six Sigma project
Yellow Belt Projects
- usually limited to identifying small projects the could benefit from improvement
Green Belts (GB)
Green belts are new team members that achieve certification after completing training in a Six Sigma course. To complete green belt training, new members must complete a relevant project that utilizes the DMAIC model outlined below. To maintain green belt certification, green belts generally complete DMAIC projects once every twelve months. Green belts are also responsible for:
- Recommending Six Sigma projects
- Participating on Six Sigma project teams
- Leading Six Sigma teams in local improvement projects
Green Belt Projects
Green belts complete six sigma projects while still holding their current job duties. Therefore, a six sigma project undertaken by a green belt could include:
- Statistical analysis to improve reliability on a reactor within the green belt's current responsibility
- Root cause analysis and elimination of quality control problems that chronically affect the green belt's department
Black Belts (BB)
Black belts are intermediate team members that employ in-depth technical expertise to achieve Six Sigma objectives. Furthermore, black belts can become temporary, full-time change agents for a moderate period of time (two-three years) to produce change using Six Sigma methods. Black belts are also responsible for:
- Demonstrating mastery of black belt knowledge
- Demonstrating proficiency at achieving results through the application of the Six Sigma approach
- Consultation for functional area Internal Process Improvement
- Coaching, Mentoring, and Recommending green belts
Black Belt Projects
Black belts complete six sigma projects outside of their previous job duties. Therefore, a six sigma project undertaken by a black belt could include:
- Plant-level process controls improvement at a facility that greatly affects the finished product at a facility
- Assessment of total warranty/quality control issues at a facility through large scale statistical data analysis and improvement
Master Black Belts (MBB)
The major duty of master black belts include acting as project leaders, as well as:
- Training and mentoring Black Belts and Green Belts
- Helping to decide large-scale Six Sigma projects
- Maintaining the quality of Six Sigma measurements
- Developing Six Sigma training
Master Black Belt Projects
Most master black belts would only be involved with directing black and/or green belts in their projects. Their effect on process would generally be limited to pointing out and suggesting large projects for appointed black belts to undertake.
To complete Six Sigma projects, belt candidates utilize the DMAIC model. DMAIC (Define, Measure, Analyze, Improve, Control) is an improvement system for existing processes falling below specification and looking for incremental improvement. DMADV (Define, Measure, Analyze, Design, Verify) is an improvement system used to develop new processes at Six Sigma quality level. Below, the steps for DMAIC and DMADV are outlined.
Table 1 - Outline of the steps used in DMAIC (improve an existing process)

Table 2 - Outline of the steps used in DMADV (develop a new process)

All charts and descriptions referenced from Pyzdek, Thomas, “DMAIC and DMADV Explained” http://www.pyzdek.com/DMAICDMADV.htm , 2003
Statistics and Six Sigma
You are probably already familiar with the concepts of average, standard deviation, and Gaussian distribution. However, they are very important concepts in Six Sigma, so they are reviewed in this section. This section also discusses analysis methods used in Six Sigma.
Average
The equation for calculating an average is shown below.
\[\bar{x}=\frac{1}{N} \sum_{i=1}^{N} x_{i}=\frac{x_{1}+x_{2}+\cdots+x_{N}}{N} \nonumber \]
where
- \(\bar{x}\) is the average
- \(xi\) is the measurement for trial \(i\)
- \(N\) is the number of measurements
This equation relates to Six Sigma because it is the value that you aim for when you are creating your product. After millions of products made, you will have a very good idea of what your exact average product specification is. The average is combined with the specification limits, which are the limits that determine if your product is in or out of spec. The wider the specification limits are, the more room for deviation from the average there is for your product. A product specification would be written like this:
\[10 ± 2\, mm \nonumber \]
Where the first number (10) represents the average and the second number (2) represents the amount of error allowable from the average without violating 4.5 standard deviations (on a long term scale). Thus, your product can range from 8 to 12 mm for this example.
The average is a good representation of the a set of data. However, the main problem it experiences is the how it is strongly influenced by outlier values. For example, say a town had a population of 50 people with an average income of $30,000 per person. Now say that a person moves into the town with an income of $1,000,000. This would move the average up to approximately $50,000 per person. However, this is not a good representation of the average income of the town. Hence, outlier values must be taken into account when analyzing data. In contrast to the mean, sometimes the median can be a good representation of a set of data. The median is defined as the middle value of a set of data are arranged in order. The median is immune to outlier values as it basically one value and is not calculated it any way so it cannot be influenced by a wide range of numbers. Both the mean and median can be taken into account when analyzing a set of data points.
Standard Deviation
The equation for standard deviation is shown below.
\[\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}} \nonumber \]
where σ = standard deviation, and the other variables are as defined for the average.
For each measurement, the difference between the measured value and the average is calculated. This difference is called the residual. The sum of the squared residuals is calculated and divided by the number of samples minus 1. Finally, the square root is taken.
The standard deviation is the basis of Six Sigma. The number of standard deviations that can fit within the boundaries set by your process represent Six Sigma. If you can fit 4.5 standard deviations within your process specifications then you have obtained a Six Sigma process for a long term scale. However, the number of errors that you can have for your process as you move out each standard deviation continues to decrease. The table below shows the percentage of data that falls within the standard deviations and the amount of defects per sigma, in terms of "Defects Per Million Opportunities" or DPMO. The percentage of errors that you are allowed is one minus the percentage encompassed by the percent of the total.
| # of Standard Deviations | % of Total | DPMO |
|---|---|---|
| 1 | 68.27 | 690,000 |
| 2 | 95.45 | 308,537 |
| 3 | 99.73 | 66,807 |
| 4 | 99.9937 | 6,210 |
| 5 | 99.99994 | 233 |
| 6 | 99.9999998 | 3.4 |
The image below shows an example data set (see #Gaussian Distribution below) with lines marking 1 to 6 standard deviations from the mean. In this example, the mean is approximately 10 and the standard deviation is 1.16.

Gaussian Distribution
The normal, or Gaussian, distribution is a family of continuous probability distributions. The normal distribution function was first introduced in 1733, and since has become the most widely used family of distribution functions in statistical analysis. These distribution functions are defined by two parameters: a location (most commonly the "mean",μ), and a scale (most commonly the "variance", σ2). The use of normal distributions in statistics can be seen as advantageous due to its ability to maximize information entropy around a given mean and variance. Information entropy is the measure of uncertainty associated with a random variable.
For the purposes of this class and Chemical Engineering applications, you can model a given set of data using the probability density function which is shown below.
\[\varphi=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) \nonumber \]
where \(\varphi) is the probability density, \(\mu\) is the average and the other variables are as defined in the above two sections.
The above PDF equation gives graphs, depending on mean and variance, similar to those below.

Above are four examples of different distributions given different values for mean and standard deviation. An important case is the standard normal distribution shown as the red line. The standard normal distribution is the normal distribution with a mean of 0 and a variance of 1. It is also important to note some special properties of probability density functions:
- symmetry about the mean, \(μ\)
- the mode and mean are both equal to the mean
- the inflection points always occur one standard deviation away from the mean, at \(μ − σ\) and \(μ + σ\)
Suppose we have a process where we make a product of a certain concentration and we have good control over the process. After analyzing a set of data from a time period we see that we have a standard deviation of only 0.01 and our product concentration is required to be within 0.05. In order to say our product is essentially defect-free, 4.5 standard deviations away from the average must be less than our required product tolerance (± 0.05). In this case 4.5 standard deviations is equal to 0.045 and our product tolerance is 0.05. This is more easily seen graphically, as seen in the figure below.

As you can see 4.5 standard deviations on either side of the averages falls just slightly inside of the required tolerances for our product. This means that 99.997% of our product will fall inside of our product tolerances.
Analysis Methods
Two ways to analyze data for similarities (percent confidence) would be running a regression analysis or an analysis of variance (ANOVA). The difference between these two methods of analysis is that the ANOVA is for comparing independent groups such as 4 different reactor compositions that are supposed to make the same product (in reality this doesn’t happen). A linear regression would be used for data that is dependent on each other, such as looking at the difference between slurry product permeabilities when a one-reactant composition in the process is changed. The percent confidence is the same as the student’s t-test, where you would want a t value (error) that is less than 0.05 to have statistically similar data.
One statistical program that is widely used in Six Sigma projects is MINITAB. MINITAB is similar to Microsoft Excel but has much greater statistical analysis capabilities. This program allows you to run linear regressions and ANOVAs by the click of an option. It also graphs not only in 2-D but 3-D as well and runs statistical analysis methods that are more in depth than those offered in Excel. MINITAB graphical and analytical tools can provide insight and information throughout the DMAIC process. MINITAB can be used to:
- Identify - visualize sources of variation and relationships among variables
- Verify - having statistical confidence behind conclusions
Key Tool Bar Descriptions on MINITAB
- File - typical of most programs - save, open, print, etc.
- Data - can subset data easily (stratification), transpose data, stach and unstack, convert text to numberic and back, code data
- Calc - calculator function - one time calc (doesn't update as you update your data)
- Stat - t-tests, regression, ANOVA, DOE, control charts, quality tools (Pareto and Gage R&R)
- Graph - plots, histogram, matrix plot
- Editor - find/replace (if you need to find items)
- Tools - options and links to some external tools
- Window - session window shows detains on what you have open
MINITAB is a powerful tool to help us understand the language of measurement and the different uses of measurement system. Some unique features of MINITAB include: Measurement System Analysis (MSA) and the Gage Reproducibility and Repeatability Study (Gage R&R). These two complicated Six Sigma analysis can be accomplished within steps using MINITAB.
Statistical Process Control
Statistical process control (SPC) is an effective method of determining whether a system has deviated from its normal statistical behavior by the use of control charts. Walter Shewhart first pioneered the use of statistical techniques when studying variations in product quality and consistency at Bell Laboratories in the early 1920’s. SPC utilizes statistical tools in the form of control charts (such as Shewhart charts) to observe the performance of the production process in order to predict significant deviations that may result. Dr. Shewhart created concepts for statistical control and the basis for control charts through a series of carefully designed experiments. While he primarily drew from pure mathematical statistical theories, he understood that data from physical processes seldom produced a normal distribution curve (a Gaussian distribution, also known as a bell curve). Shewhart determined that every process displays variation: some display controlled variation that is natural to the process, while others display uncontrolled variation that is not always present in the process causal system.
SPC, most often used for manufacturing processes, is used in conjunction with experimental designs, process capability analyses, and process improvement plans to monitor product quality and maintain process targets. Six Sigma programs often depend on statistical process controls to provide their data with supportive information. If a process falls outside its preferred operating range, the statistical control can help you determine where and why the process failed.
Benefits of the SPC Method:
- Provides surveillance and feedback for keeping processes in control
- Signals when a problem with the process has occurred
- Detects assignable causes of variation
- Accomplishes process characterization
- Reduces need for inspection
- Monitors process quality
- Provides mechanism to make process changes and track effects of those changes
- Once a process is stable (assignable causes of variation have been eliminated), provides process capability analysis with comparison to the product tolerance
Capabilities of the SPC Method:
- All forms of SPC control charts
- Variable and attribute charts
- Average (X), Range (R), standard deviation (s), Shewhart, CuSum, combined Shewhart-CuSum, exponentially weighted moving average (EWMA)
- Selection of measures for SPC
- Process and machine capability analysis (Cp and Cpk)
- Process characterization
- Variation reduction
- Experimental design
- Quality problem solving
- Cause and effect diagrams
SPC is used to monitor the consistency of processes used to manufacture a product as designed. It aims to get and keep processes under control. No matter how good or bad the design, SPC can ensure that the product is being manufactured as designed and intended. Thus, SPC will not improve a poorly designed product's reliability, but can be used to maintain the consistency of how the product is made and, therefore, of the manufactured product itself and its as-designed reliability.
Methods and Control Charts
Control charts are the basis of statistical process controls methodologies, and are used to distinguish between random/uncontrollable variations and controlled/correctable variations in a system. Control chart detects and monitors process variation over time. It also plays a role as a tool for ongoing control of a process. There are many types of SPC control charts, though centering charts are used most often. The remainder of this article will focus on the different types of centering and dispersion charts. Figure 1 displays single point centering charts and Figure 2 displays subgroup sampling charts. Each figure has a brief description of the chart type within each of the two chart families (centering and dispersion). In the centering chart, the centerline is given by the average of the data samples, where as in the dispersion chart the centerline is the frequency distribution from that average.


A very useful type of centering chart is the Xbar chart, also known as the Shewhart chart mentioned earlier in the article. Figure 3 gives an example of an Xbar chart (on top), as well as an example of a dispersion chart (on bottom). The charts are used in combination with a system of rule based checks to determine whether the system is in statistical control. These rules can be seen in Figure 4 for both the single point centering and subgroup sampling methods. Using these rules, one can inspect a given chart over a period of time and determine whether the system is in control. If the system is not in control they must then check the controllable aspects of the system to see where the problem is occurring.


Note: We only need to see if any one of the criteria objectives are achieved to claim that the system is statistically out of control.
As can be seen from the figures above, the primary tool of SPC is the control chart. Several different descriptive statistics are used in control charts along with several different types of control charts that test for different causes of failure. Control charts are also used with product measurements to analyze process capability and for continuous process improvement efforts.
KLMM Industries has recent data on their widget making process. The data is shown below. The allowable range of widget width is 19.5-22.5 cm.

- Please from this data calculate the mean and write the mean with its allowable range?
- Next calculate the standard deviation for this data.
- Does this process fall within 4.5 standard deviations?
- 6 standard deviations?
Solution
a
\[\bar{x}=\frac{1}{N} \sum_{i=1}^{N} x_{i}=\frac{x_{1}+x_{2}+\cdots+x_{N}}{N} \nonumber \]
This is also calculated using the average function in excel, from this the average is calculated to be 20.9945
b
\[\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\bar{x}\right)^{2}} \nonumber \]
This is also calculated using the STDEV function in excel, from this the standard deviation is calculated to be 0.3206
3) Yes
4) No

A chemical engineer at Cool Processes Inc. is in charge of monitoring the flowrate of the cooling water for a reaction. He's new at the company and has asked you for your input. He says that the process is currently in statistical control and does not need to be changed. Below is the centering control chart he has made of the process. Do you agree or disagree with his opinion? Explain.
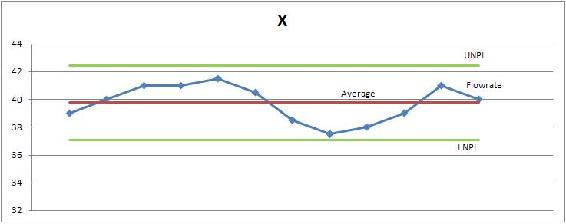
Solution
Even though the process appears to be within a reasonable range of oscillation, and none of the data points are exceeding the process limitations, the system is not in statistical control. Centering (X) charts show that a process is not in statistical control if "three or more consecutive points fall on the same side of the centerline and all are located closer to the control limit than to the centerline."(Liptak 2006). The data points circled in the plot below violate that rule.

This example will also serve as a small tutorial for using Minitab.
ABC Production is coming out with a new product. One of the chemical engineers has hypothesized that the product thickness is dependent on the process temperature and the concentration of “compound Z.” There are currently controls regulating the temperature between 77 and 80°C, and the concentration of Z between 0.0066 and .0073 g/L. Product specifications require that the thickness limits are 1.94 to 2.10 cm. You have been assigned the task of determining if these are good parameters to control. Use the data from random samples and use Minitab with linear regression to make your conclusion.

Solution
Conclusion: Temperature is much more influential on the thickness than the concentration, so it may be more worthwhile to refine the temperature control than to focus on the concentration controllers. Another option would be to investigate other system parameters (i.e., time in reactor, pressure, etc.) to see if they hold more influence on the thickness.
Using Minitab
1) Open Minitab and input data

2) Select the “Regression” option from the “Stat” menu and the “Regression” tab
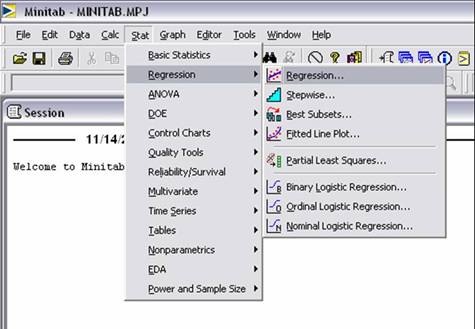
3)The regression window will open; add the “thickness” column for the response, and the Temperature and Concentration columns to the predictors.

4)Click the “Options” button and select “PRESS and predicted R-squared,” then click “OK” on both dialog boxes.

5)The results will appear in the session window:
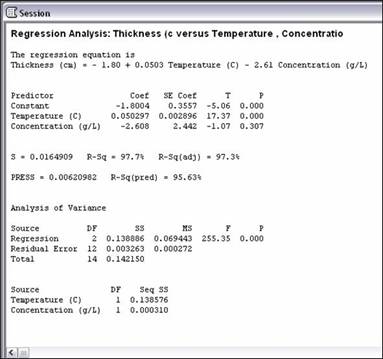
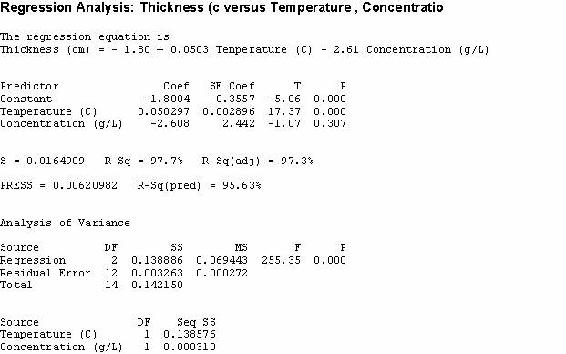
Interpreting the data
Some of the most important values in the returned data are the p values. These values test the null hypothesis that there is no effect by the inputs (concentration and temperature here) on the output (thickness). The lower the value of p, the more correlation there is between each variable and the result. In this case, the regression has a p value of 0 (under analysis of variance), so the model is significant and at least one of the coefficients is not zero. The p values in the predictor section show a zero value for Temperature (high correlation with thickness) but a 0.3 value for concentration (low correlation with thickness. This indicates that the concentration controller is not significant.
Next we will in spect the R2 values. The R-Sq value of 97.7% indicates that the predictors (concentration and temperature) explain that percent of the variance in thickness. The adjusted value (97.3%) accounts for the number of predictors (here, 2) in the model. Since both are high, the model that is given at the beginning of the readout fits the data well.
The predicted R value is also important because it measures the amount of overfit of the model. If this value were not close to the R-Sq value, then the model would only be applicable for this set of data points but would probably not be accurate for any other combination of data points. Since the “R-Sq(pred)” value is close to the R-Sq value, this model is good.
References
- Instrument Engineer's Handbook:Process Control and Optimization Vol.IV (2005) edited by Liptak, Bela G. New York: Taylor and Francis Group
- Perlmutter, Barry (2005) A Six Sigma Approach to Evaluating Vacuum Filtration Technologies BHS-Filtration INC.
- Chambers & Wheeler Understanding Statistical Process Control Tennessee: SPC Press


