13.8: Continuous Distributions- normal and exponential
- Page ID
- 22529
Authors: Navin Raj Bora, Dallas Burkholder, Nina Mohan, Sarah Tschirhart
Introduction
Random variables whose spaces are not composed of a countable number of points but are intervals or a union of intervals are said to be of the continuous type. Continuous distributions are probability models used to describe variables that do not occur in discrete intervals, or when a sample size is too large to treat each individual event in a discrete manner (please see Discrete Distributions for more details on discrete distributions). The main difference between continuous and discrete distributions is that continuous distributions deal with a sample size so large that its random variable values are treated on a continuum (from negative infinity to positive infinity), while discrete distributions deal with smaller sample populations and thus cannot be treated as if they are on a continuum. This leads to a difference in the methods used to analyze these two types of distributions: continuous and discrete distributions is continuous distributions are analyzed using calculus, while discrete distributions are analyzed using arithmetic. There are many different types of continuous distributions including some such as Beta, Cauchy, Log, Pareto, and Weibull. In this wiki, though, we will only cover the two most relevant types of continuous distributions for chemical engineers: Normal (Gaussian) distributions and Exponential distributions.
In chemical engineering, analysis of continuous distributions is used in a number of applications. For example in error analysis, given a set of data or distribution function, it is possible to estimate the probability that a measurement (temperature, pressure, flow rate) will fall within a desired range, and hence determine how reliable an instrument or piece of equipment is. Also, one can calibrate an instrument (eg. temperature sensor) from the manufacturer on a regular basis and use a distribution function to see of the variance in the instruments' measurements increases or decreases over time.
Normal Distributions
What is a Gaussian (normal) distribution curve?
A Gaussian distribution can be used to model the error in a system where the error is caused by relatively small and unrelated events.
This distribution is a curve which is symmetric about the mean (i.e. a Bell shaped curve) and has a range measured by standard deviations above and below the mean of the data set (please see Basic Statistics for a further discussion on these statistical parameters). To better explain, consider that a certain percentage of all data points will fall within one standard deviation of the mean. Likewise, more data points will fall within two standard deviations of the mean, and so on. However, under this model it would require an infinite range to capture ALL the data points thus presenting a minor difficulty in this appraoch.
The figure below is a possible Gaussian distribution, where the mean (μ) is 10 and standard deviation (σ) is 2. F(x) is the number of times a certain value of x occurs in the population. The mean is simply the numerical average of all the samples in the population, and the standard deviation is the measure of how far from the mean the samples tend to deviate. The following sections explain how and why a normal distribution curve is used in control and what it signifies about sets of data.
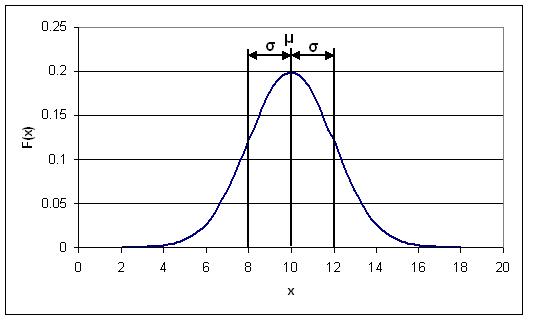
The Probability Density Function (PDF) for a normal distribution
As was mentioned in the Introduction section, distribution curves can be used to determine the probability, P(x), of a certain event occurring. When this is done, the distribution curve is known as a Probability Density Function (PDF). In the figure shown above, the x-axis represents the range of possible events (eg. the range of ages in a sample population or the magnitude of noise generated by a temperature sensor). The y-axis represents the number of times a certain x value occurs in a population. The PDF can be described mathematically as follows:
In some cases, it might not be necessary to know the probability of just one event occurring. Rather, you may want to know the probability of a range of events (eg. what is the probability that the noise generated by my temperature sensor will fall in the range of 5-10 Hz?). When this happens, you must integrate the above PDF over the desired range, in the following manner:
where k1 and k2 are the limits of your desired range. This integral results in the following expression:
![(k_1<x<k_2)=\frac{1}{2}(Erf[\frac{k_2-\mu}{\sigma\sqrt{2}}]-Erf[\frac{k_1-\mu}{\sigma\sqrt{2}}])](https://eng.libretexts.org/@api/deki/files/19463/image-778.png?revision=1)
The Erf function can be found in most scientific calculators and can also be calculated using tables of Erf[] values. For example, its use here parallels what we learned in ChE 342, Heat and Mass Transfer. Determine the value inside the brackets of the erf function through simple arithmetic, then take this value and find the corresponding Erf number from a table. Finally use this value in the calculation to determine the probability of a certain point, x, falling within a range bound from k1 to k2.
Sample Calculation
Given a data set with an average of 20 and a standard deviation of 2, what is the probability that a randomly selected data point will fall between 20 and 23?
Solution 1
To solve simply substitue the values into the equation above. This yeilds the following equation:
![(20<x<23)=\frac{1}{2}(Erf[\frac{23-20}{2\sqrt{2}}]-Erf[\frac{20-20}{2\sqrt{2}}])](https://eng.libretexts.org/@api/deki/files/19465/image-779.png?revision=1)
![(20<x<23)=\frac{1}{2}(Erf[1.061]-Erf[0])](https://eng.libretexts.org/@api/deki/files/19466/image-780.png?revision=1)
These Erf values must be looked up in a table and substituted into the equation. Doing this yeilds
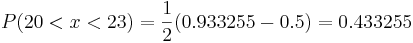
Thus there is a 43.3255% chance of randomly selecting a number from the data set with a value between 20 and 23.
Graphically speaking, the PDF is just the area under the normal distribution curve between k1 and k2. So, for the distribution shown above, the PDF for 8<x<12 would correspond the area of the orange shaded region in the figure below:
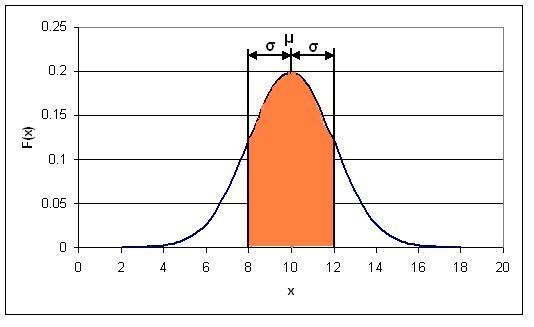
Solution 2
Alternatively, rather than using the error function, Mathematica's built-in probability density function can be used to solve this problem. This probability density function can be applied to the normal distribution using the syntax shown below.
NIntegrate[PDF[NormalDistribution[μ,σ],x],{x,x1,x2}]
In this syntax, μ represents the mean of the distribution, σ represents the standard deviation of the distribution, and x1 and x2 represent the limits of the range.
This function can be applied to this problem as shown below.
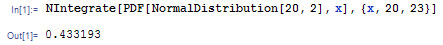
This shows that the probability of a randomly selected data point falling between 20 and 23 is 0.4332, or 43.32%. As expected, this value calculated using the built-in probability density function in Mathematica matches the value calculated from using the error function. Mathematica provides a faster solution to this problem.
An important point to note about the PDF is that when it is integrated from negative infinity to positive infinity, the integral will always be equal to one, regardless of the mean and standard deviation of the data set. This implies that there is a 100% chance that your random variable x will fall between negative infinity and positive infinity. Likewise, the integral between negative infinity and the mean is 0.5, or there is a 50% chance of finding a value in this region due to the symmetric nature of the distribution.
The Cumulative Density Function (CDF) for a normal distribution
To transition our arguement to a more holistic perspective regarding the probability density function for a normal distribution, we present the cumulative density function, which represents the integral (area under the curve) of the PDF from negative infinity to some given value on the y- axis of the graph incrementally accoring to the x axis, which remains the same as before. Because of this type of definition, we may circumvent the rigorous error function analysis presented above by simply subtracting one CDF points from another. For example, if engineers desire to determine the probability of a certain value of x falling within the range defined by k1 to k2 and posses a chart feauturing data of the relevant CDF, they may simply find CDF(k2)- CDF(k1) to find the relevant probability.
The Cumulative Density Function (CDF) is simply the probability of the random variable, x, falling at or below a given value. For example, this type of function would be used if you wanted to know the probability of your temperature sensor noise being less than or equal to 5 Hz. The CDF for a normal distribution is described using the following expression:
![(-\infty<x<k)=\frac{1}{2}(Erf[\frac{k-\mu}{\sigma\sqrt{2}}]+1)](https://eng.libretexts.org/@api/deki/files/19474/image-782.png?revision=1)
where k is the maximum allowable value for x.
The main difference between the PDF and CDF is that the PDF gives the probability of your variable x falling within a definite range, where the CDF gives the probability of your variable x falling at or below a certain limit, k. The following figure is the CDF for a normal distribution. You'll notice that as x approaches infinity, the CDF approaches 1. This implies that the probability of x falling between negative and positive infinity is equal to 1.
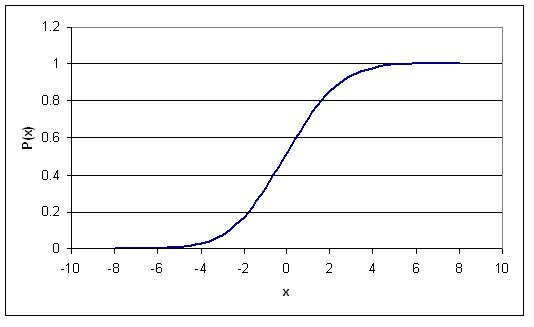
Standard Normal Distribution
A special type of probability distribution curve is called the Standard Normal Distribution, which has a mean (μ) equal to 0 and a standard deviation (σ) equal to 1.
This simplified model of distribution typically assists engineers, statisticians, business strategists, economists, and other interested professionals to model process conditions, and to associate the attention and time needed to adress particular issues (i.e. higher probability for a failed condition necessitate additional attention, etc.). Also, our grades in many of the courses here at the U of M, both in and outside of the college of engineering, are based either strictly or loosely off of this type of distribution. For example, the B range typically falls within +/- of one standard deviation.
The following figure is a Standard Normal Distribution curve:
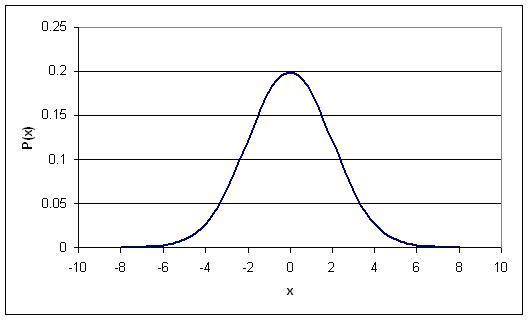
The benefit of the standard normal distribution is it can be used in place of the Erf[] function, if you do not have access to a scientific calculator or Erf[] tables. To use the Standard Normal Distribution curve, the following procedure must be followed:
1.Perform a z-transform. This is a transformation which essentially normalizes any normal distribution into a standard normal distribution. It is done using the following relationship:
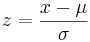
Mathematically speaking, the z transform normalizes the data by changing all the raw data points into data points that dictate how many standard deviations they fall away from the mean. So, regardless of the magnitude of the raw data points, the standardization allows multiple sets of data to be compared to each other.
2.Use a standard normal table to find the p-value. A standard normal table has values for z and corresponding values for F(x), where F(x) is known as the p-value and is just the cumulative probability of getting a particular x value (like a CDF). A standard normal table may look like the following table (it should be noted that if you are dealing with a Standard Normal Table that contains only positive z values, the following property can be used to convert your negative z values into positive ones: F(-z)=1-F(z)):
Table 1: Standard Normal Table
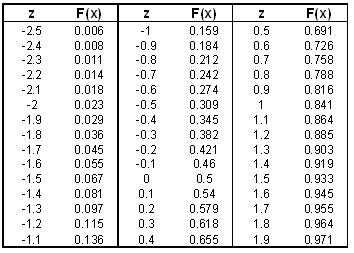
A more detailed standard normal table can be found here (Note: This table is the same table used in the 'Basic Statistics' wiki).
3. What if I want the probability of z falling between a range of x=a and x=b?. First, find your two z values that correspond to a and b. So these would be 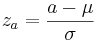 and
and 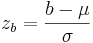 , respectively. The probability of x falling in between a and b is just: F(zb) – F(za), where F(zb) and F(za) are found from the standard normal tables.
, respectively. The probability of x falling in between a and b is just: F(zb) – F(za), where F(zb) and F(za) are found from the standard normal tables.
Sample Calculation
Lets take the same scenario as used above, where you have a data set with an average of 20 and standard deviation of 3 and calculate the probability of a randomly selected data point being between 20 and 23.
Solution
To do this simply subtract the two Z scores:
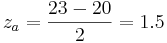

These Z scores correspond to probabilities of 0.933 and 0.5 respectively. Their difference, 0.433, is the probability of a randomly selected value falling between the two. Notice that this is almost identical to the answer obtained using the Erf method. Note that obtaining this answer also required much less effort. This is the main advantage of using Z scores.
Properties of a Normal Distribution
There are several properties for normal distributions that become useful in transformations.
1 If X is a normal with mean μ and σ2 often noted  then the transform of a data set to the form of aX + b follows a
then the transform of a data set to the form of aX + b follows a 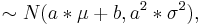 .
.
2 A normal distribution can be used to approximate a binomial distribution (n trials with probability p of success) with parameters μ = np and σ2 = np(1 − p). This is derived using the limiting results of the central limit theorem.
3 A normal distribution can be used to approximate a Poisson distribution (parameter λ) with parameters μ = σ2 = λ. This is derived using the central limit theorem.
4 The a sum of random variables following the same normal distribution ˜N(nμ,nσ2). This result shows how the sample mean 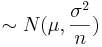 .
.
5 The square of a standard normal variable is a chi-squared variable with one degree of freedom.
6 Combining 4 and 5 yields the sum of n squared standard normal variables is a chi-squared variable with n degrees of freedom. This has application for chi-square testing as seen other sections of this text.
Exponential Distribution
The exponential distribution can be thought of as a continuous version of the geometric distribution without any memory. It is often used to model the time for a process to occur at a constant average rate. Events that occur with a known probability for a given x value build the theory developed previously (i.e. F(x) vs. x, F(x) in this case is different than before), where x may indicate distance between mutations on a DNA strand., for one example application, rate of instrument failure, or time required for a radioactive particle to decay (the decay RATE) for the below applications.
However, do remember that the assumption of a constant rate rarely holds as valid in actuality. The rate of incoming phone calls differs according to the time of day. But if we focus on a time interval during which the rate is roughly constant, such as from 2 to 4 p.m. during work days, the exponential distribution can be used as a good approximate model for the time until the next phone call arrives.
One can implement the exponential distribution function into Mathematica using the command: ExponentialDistribution[lambda].
Or, for a more grass-roots understanding of the function reference the following website, detailing the number of sharks seen in area one square mile in different one hour time periods. Use the "Fish" button to run the applet. To change the parameter lambda, type in the value and hit the "Clear" button.
www.math.csusb.edu/faculty/stanton/m262/poisson_distribution/Poisson_old.html
The Probability Density Function (PDF)
A few notes are worth mentioning when differentiating the PDF from the two-parameter Exponential Distribution function. As λ is decreased in value, the distribution is stretched out to the right, and as λ is increased, the distribution is pushed toward the origin. This distribution has no shape parameter as it has only one shape, i.e. the exponential, and the only parameter it has is the failure rate, λ. The distribution starts at T = 0 at the level of f(T = 0) = λ and decreases thereafter exponentially and monotonically as T increases, and is convex. The PDF for an exponential distribution is given in the form below, where λ is the rate parameter and x is random variable:
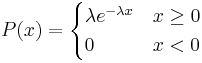
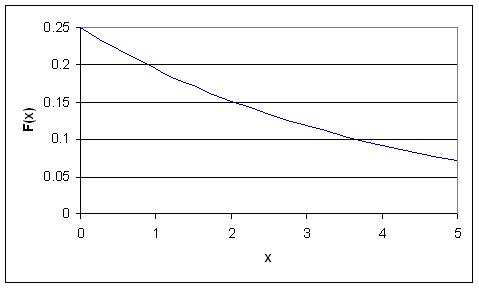
Here, x could represent time while the rate parameter could be the rate in which decay occurs. The rate parameter must be constant and greater than 0. The PDF decreases continuously in this diagram because of its definition as a decay example. Exponential decay typically models radioactive particles which lose mass per unit of time. Thus F(x) represents the mass of the particle with x equalling elapsed time since the start of the decay. As time passes, the mass falls due to radioactive decay (particle emits radiation as a form of energy release, any energy that results subtracts from mass, E = MC2).
The Cumulative Distribution Function (CDF)
The CDF for an exponential distribution is expressed using the following:
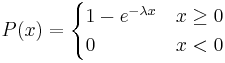
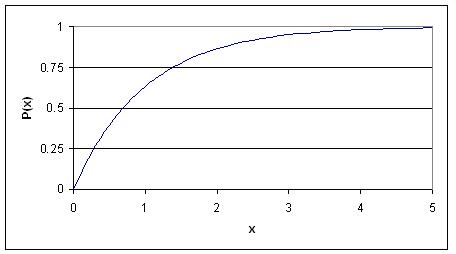
Following the example given above, this graph describes the probability of the particle decaying in a certain amount of time (x).
Properties of the Exponential Distribution
Among the distribution functions, the exponential distribution funtion has two unique properties, they are the memoryless property and a constant hazard rate.
--The Memoryless Property--
If a random variable, X, survived for "t" units of time, then the probability of X surviving an additional "s" units of time is the same as the probability of X suriving "s" units of time. The random variable has "forgotten" that it has survived for "t" units of time, thus this property is called the "memoryless" property.
A random variable, X, is memoryless if
P { X > s+t | X > t} = P { X > s } for all s,t 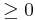 (1)
(1)
From using (1) above and the definition of conditional probability:
s, X > t)}{P (X > t)} = P(x > s)" src="/@api/deki/files/19503/image-794.png">(2)
and so:
P{X > s+t} = P{X > s}P{X > t} (3)
to prove the above property, we suppose that there is a function such that F(x)=P{X > x}.
by equation 3 above, we have
F(x+t) = F(s)F(t) (4)
By elementary calculus, the only continuous solution for this kind of functiona equation is
F(x) = e − λx (5)
It is thus proven the only distribution that can solve equation (4), or the memoryless property, is an exponential function.
--The Constant Hazard Rate Property--
Suppose the random variable, X, survived for "t" units of time, and r(t) represents the conditional probability that the t-year-old variable will fail. Mathematically the hazard rate, or the failure rate, is defined as:
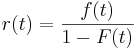 (6)
(6)
For the exponential distribution, the hazard rate is constant since
f(t) = e − λx,
and
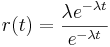
r(t) = λ
the above proved that r(t) is constant for exponential distribution.
Standard Exponential Distribution
When an exponential distribution has λ = 1, this is called the standard exponential distribution. The equation and figure for this function is described below:
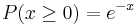
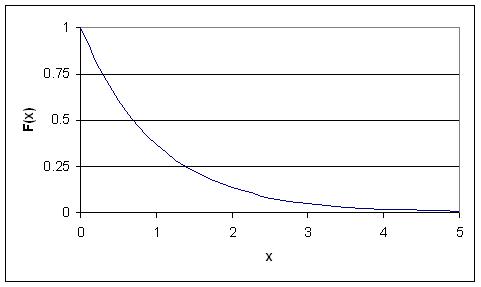
This type of distribution is a way of standardizing your graph. This parallels our previous example of standard normal distribution, however, since time is now the x variable, it may not be negative (as an assumption of our hypothetical scenario). Thus, decay occurs only for positive time (as the radioactive particle emits mass).
Worked out Example 1
You are the lead process engineer for a leading pharmaceutical company, and your newest responsibility is to characterize one of your bioreactors. Part of this characterization is to determine the temperature variance within the reactor during the last step in an isothermal reaction. After taking data during this reaction for two weeks straight, you determine that the average temperature of the reaction is 30 C, with a standard deviation of your set of data being 3 C. Also, the data fits an normal distribution (ie. it is not skewed either side of the average) The higher-ups, ie. the ones who give you the raises, decide that this reactor needs to operate within 6 degrees of its average operating temperature at least 60% of the time. Given the data that you have taken, does the reactor meet these standards, or will you be pulling some 80 hour weeks in the near future trying to fix the process?
Solution
The information given in this problem is as follows:
- Average: 30
- Standard Deviation: 3
- We want to find the probability of the temperature falling between 24 and 36 C
Using the PDF for a Normal Distribution, we can say that:
![(24<T<36) = \frac{1}{2}(Erf[\frac{36-30}{3\sqrt{2}}]-Erf[\frac{24-30}{3\sqrt{2}}])=\frac{1}{2}(Erf(1.4142)-Erf(-1.4142))](https://eng.libretexts.org/@api/deki/files/19513/image-798.png?revision=1)
This expression can easily be solved using a table of Erf[] values as well as the property of the Erf function that states Erf(-x)=-Erf(x). Another simple approach would be to use Mathematica with the syntax shown below.

Solving for P(24<T<36), we get the probability of the temperature falling within two standard deviations of the average to be about 95% Since this value is much greater than the required 60%, you can be rest assured that your reactor is running well.
Worked out Example 2
You are an engineer at a plant producing a volatile fuel. In your first week on the job both the primary control and redundancy control fail in the same day, necessitating the significant inconvenience of shutting down the reactor in order to prevent a much more inconvenient explosion. Your boss wants you to decide whether to simply replace both sensors or add an additional sensor to ensure that such problems are avoided in the future. While adding another sensor would certainly help solve the problem there is an extra cost associated with purchasing and installing the sensor. A very helpful fellow engineer with a penchant for statistics helps you out by informing you that these dual instrument failures occur at the rate of one per 3.8 * 108 hours. What is the probability that this type of failure will happen again in the next 50 years (the estimated life of the plant)? What is your recommendation to your boss?
Solution
Because you are given the probability of the event occuring and are interested in the amount of time separating two events using an exponential distribution is appropriate. To solve this you use the CDF expression:
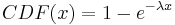
In this case λ is given in hours and x in years, so you must first convert one of the units. Also the rate give is in events per hour. λ must be entered into the equation as the inverse (probability per time unit). Entering the appropriate numbers yeilds the following equation:
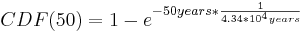
There is a 0.115% chance of both sensors failing in the same day sometime in the next 50 years. Based in this data you can conclude that you are probably safe simply replacing the two sensors and not adding a third.
Worked Out Example 3
You work at a chemical plant that uses the famous reaction A + B -> C to produce C. As part of your process you operate a mixing tank to dilute reactant A before sending it to the reactor. Reactant B is a byproduct from another process in the plant and comes in at a variable rate. This causes fluctuations in the level of the mixing tank for reactant A as the flow in and out of the tank has to be adjusted. In the past this has caused overflows in mixing tank A that your boss has tasked you with avoiding. You'ved decided the easiest way to avoid overflows is to simply buy a larger mixing tank. Currently the mixing tank is 50 gallons. After some experimentation you find the normal operating conditions of the tank are 45 gallons of reactant A with a 3 gallon standard deviation. However, to minimize costs the tank needs to be as small as possible. What is smallest tank you can buy that avoids overflows 99.99% of the time?
Solution:
Known values:
μ = 45gal.
σ = 3gal.
Using a z-table you find that the smallest z-value that gives an F(x) of 0.9999 is 3.71. You then rearrange the z equation given below to solve for x and plug in all known values.
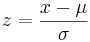
x = z * σ + μ
x = 3.71 * 3 + 45 = 56.1
In order to prevent overflows 99.99% of the time the smallest tank that can be used is 56.1 gal.
Multiple Choice Question 1
Please briefly summarize the primary difference between continuous and discrete distributions, and their respective methods of analysis:
a. Continuous distributions and discrete distributions are always both analyzed through calculus methods only. Continuous distributions are distinct from discrete distributions in that the sample size is too small to treat each individual event in a discrete manner.
b. Continuous distributions are analyzed by applying calculus methods whereas discrete distributions are commonly addressed via arithmetic methods. Continuous distributions are distinct from discrete distributions in that the sample size is too large to treat each individual event in a discrete manner.
c. By performing a standard z- transform, the interested student may begin the process of characterizing the probability of z falling between the specific range from x = ‘a’ and x = ‘b’.
d. Error functions allow us to determine the likelihood of a data point falling within certain bounds without having to complete the rigorous of the probability distribution function. Continuous distributions may be addressed in this manner since their sample size is too confusing to be addressed in a discrete manner.
Multiple Choice Question 2
Please explain the primary philosophical difference between the parameters of the probability distribution function (PDF) and the cumulative distribution function (CDF).
a. Who uses the word philosophical in a chemical engineering problem? The author of this question is most likely confused and trying too hard, so I will protest by not answering.
b. The PDF and CDF are identical in application, and as such, must also have identical parameters.
c. The PDF and CDF both commonly measure the probability of sensor noise being at or below a specific value. They are different in the fact that the CDF contains a specific range of use, ranging from k1 to k2, whereas the PDF does not, as it rises from negative infinity to a value, k.
d. The major difference the PDF and CDF is that the PDF provides the probability of the variable x falling within a defined range. Alternatively, CDF gives the probability of the variable x falling at or below a certain limit, k.
Sage's Corner
Therapeutic Insulin Production
www.youtube.com/v/b3aDqdOzP5I
A Brief Problem on Continuous Exponential Distribution Functions
video.google.com/googleplayer...13000402551106
A copy of the slides can be found here:Slides without narration
Normal Distribution Functions in Excel
If YouTube doesn't work, click here Normal Distribution Functions in Excel
References
- Gernie, L. and W. Smith "Cartoon Guide to Statistics" Harper Perennial, c. 1993


