21.7: Rank-One <mu>

Although we do not have methods for computing \(\mu\) exactly, there is one particular situation where this is possible. This situation occurs if \(M\) has rank 1, i.e

\[M=a b^{*}\nonumber\]

where \(a, b \in \mathbb{C}^{n}\). Then it follows that \(\mu\) with respect to \(\Delta_{0}\) containing complex diagonal perturbations is given by

\[\frac{1}{\mu(M)}=\inf _{\Delta \in \Delta_{0}}\left\{\sigma_{\max }(\Delta) \mid \operatorname{det}(I-M \Delta)=0\right\}\nonumber\]

However, 

\[\begin{aligned}
\operatorname{det}(I-M \Delta) &=\operatorname{det}\left(I-a b^{*} \Delta\right) \\
&=\operatorname{det}\left(I-b^{*} \Delta a\right)
\end{aligned}\nonumber\]

\[\begin{array}{l}
=\operatorname{det}\left(I-\left[\Delta_{1} \cdots \Delta_{n}\right]\left[\begin{array}{c}
\overline{b_{1}} a_{1} \\
\overline{b_{2}} a_{2} \\
\vdots \\
b_{n} a_{n}
\end{array}\right]\right) \\
=  1-\left[\Delta_{1} \cdots \Delta_{n}\right]\left[\begin{array}{c}
b_{1} a_{1} \\
b_{2} a_{2} \\
\vdots \\
b_{n} a_{n}
\end{array}\right]
\end{array}\nonumber\]

and \(\sigma_{\max }(\Delta)=\max _{i}\left|\Delta_{i}\right|\). Hence,

\[\frac{1}{\mu(M)}=\inf _{\Delta_{1}, \ldots, \Delta_{n}}\left\{\max _{i}\left|\Delta_{i}\right|\left[\left[\Delta_{1} \cdots \Delta_{n}\right]\left[\begin{array}{c}
\overline{b_{1}} a_{1} \\
b_{2} a_{2} \\
\vdots \\
b_{n} a_{n}
\end{array}\right]=1\right\}\right.\nonumber\]

Optimizing the RHS, it follows that (verify)

\[\frac{1}{\mu(M)}=\frac{1}{\sum_{i=1}^{n}\left|\overline{b_{i}} a_{i}\right|} \leftrightarrow \mu(M)=\sum_{i=1}^{n}\left|\overline{b_{i}} a_{i}\right|\nonumber\]

Notice that the SISO robust disturbance rejection problem is a rank-one problem. This follows since

\[M=\left[\begin{array}{c}
-W_{1} K \\
W_{2}
\end{array}\right]\left[\frac{P_{0}}{1+P_{0} K} \quad \frac{1}{1+P_{0} K}\right]\nonumber\]

Then

\[\mu(M(j \omega))=\left|\frac{W_{1} P_{0} K}{1+P_{0} K}(j \omega)\right|+\left|\frac{W_{2}}{1+P_{0} K}(j \omega)\right|\nonumber\]

which is the condition we derived before.

Coprime Factor Perturbations

Consider the class of SISO systems

\[\Omega=\left\{\frac{N(s)}{D(s)} \mid N=N_{0}+\Delta_{1} W_{1}, D=D_{0}+\Delta_{2} W_{2},\left\|\Delta_{i}\right\|<1\right\}\nonumber\]

where the nominal plant is \(N_{0}/D_{0}\) with the property that both \(N_{0}\) and \(D_{0}\) are stable with no common zeros in the RHP. Assume that \(K\) stabilizes \(N_{0}/D_{0}\). This block diagram is shown in Figure 21.7.

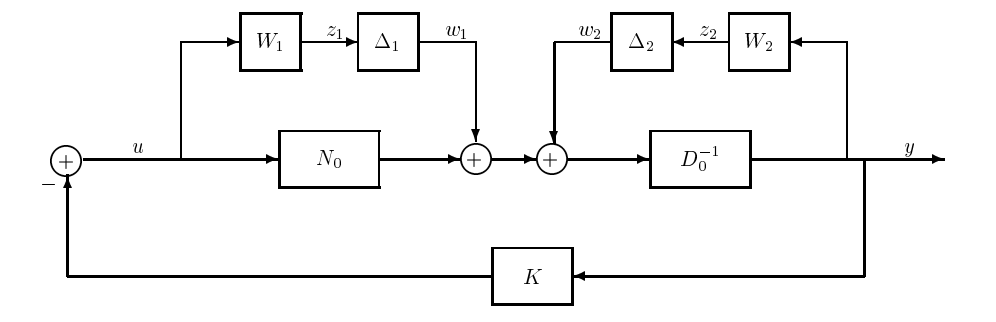
Figure 21.7: Coprime Factor Perturbation Model 

The closed loop block diagram can be mapped to the \(M- \Delta\) diagram where

\[\begin{aligned}
M &=\left[\begin{array}{cc}
-\frac{W_{1} K}{D_{0}+N_{0} K} & -\frac{W_{1} K}{D_{0}+N_{0} K} \\
\frac{W_{2}}{D_{0}+N_{0} K} & \frac{W_{2}}{D_{0}+N_{0} K}
\end{array}\right] \\
&=\left[\begin{array}{c}
-\frac{W_{1} K}{D_{0}+N_{0} K} \\
\frac{W_{2}}{D_{0}+N_{0} K}
\end{array}\right] [1 \ 1]
\end{aligned}\nonumber\]

Hence, \(M\) has rank 1 and

\[\mu(M(j \omega))=\left|\frac{W_{1} K}{D_{0}+N_{0} K}\right|+\left|\frac{W_{2}}{D_{0}+N_{0} K}\right|\nonumber\]

Robust Hurwitz Stability of Polynomials with Complex Perturbations

Another application of the structured singular value with rank one matrices is the robust stability of a family of polynomials with complex perturbations of the coeffcients. In this case let \(\delta =\left[\begin{array}{cccc}
\delta_{n-1} & \delta_{n-2} & \ldots & \delta_{0}
\end{array}\right]^{T}\) and consider the polynomial family

\[P(s, \delta)=s^{n}+\left(a_{n-1}+\gamma_{n-1} \delta_{n-1}\right) s^{n-1}+\ldots+\left(a_{0}+\gamma_{0} \delta_{0}\right)\nonumber\]

where \(a_{i}\), \(\gamma_{i}\), and \(\delta_{i} \in \mathbb{C}\) and \(\left|\delta_{i}\right| \leq 1\). We want to obtain a condition that is both necessary and sufficient for the Hurwitz stability of the entire family of polynomials \(P(s, \delta)\). We can write the polynomials in this family as

\[P(s, \delta)=P(s, 0)+\tilde{P}(s, \delta)\label{21.20}\]

\[=\left(s^{n}+a_{n-1} s^{n-1}+\ldots+a_{0}\right)+\left(\gamma_{n-1} \delta_{n-1} s^{n-1}+\ldots+\gamma_{0} \delta_{0}\right)\label{21.21}\)

which can also be rewritten as

\[P(s, \delta)=P(s, 0)+\left[\begin{array}{ccc}
1 & 1 & \ldots 1
\end{array}\right]\left[\begin{array}{ccccc}
\delta_{n-1} & 0 & 0 & \ldots & 0 \\
0 & \delta_{n-2} & 0 & \ldots & 0 \\
\vdots & & \ddots & & \vdots \\
& & & \delta_{1} & 0 \\
0 & 0 & \ldots & 0 & \delta_{0}
\end{array}\right]\left[\begin{array}{c}
\gamma_{n-1} s^{n-1} \\
\gamma_{n-2} s^{n-2} \\
\vdots \\
\gamma_{1} s \\
\gamma_{0}
\end{array}\right]\nonumber\]

We assume that the center polynomial \(P(s, 0)\) is Hurwitz stable. This implies that the stability of the entire family \(P(s, \delta)\) is equivalent to the condition that

\[1+\frac{1}{P(j \omega, 0)}\left[\begin{array}{ccc}
1 & 1 & \ldots 1
\end{array}\right]\left[\begin{array}{ccccc}
\delta_{n-1} & 0 & 0 & \ldots & 0 \\
0 & \delta_{n-2} & 0 & \ldots & 0 \\
\vdots & & \ddots & & \vdots \\
& & & \delta_{1} & 0 \\
0 & 0 & \ldots & 0 & \delta_{0}
\end{array}\right]\left[\begin{array}{c}
\gamma_{n-1}(j \omega)^{n-1} \\
\gamma_{n-2}(j \omega)^{n-2} \\
\vdots \\
\gamma_{1}(j \omega) \\
\gamma_{0}
\end{array}\right] \neq 0\nonumber\]

for all \(\omega \in \mathbb{R}\) and \(\left|\delta_{i}\right| \leq 1\). This is equivalent to the condition that

\[\operatorname{det}\left(I+\frac{1}{P(j \omega, 0)}\left[\begin{array}{c}
\gamma_{n-1}(j \omega)^{n-1} \\
\gamma_{n-2}(j \omega)^{n-2} \\
\vdots \\
\gamma_{1}(j \omega) \\
\gamma_{0}
\end{array}\right]\left[\begin{array}{lll}
1 & 1 & \ldots 1
\end{array}\right] \Delta\right) \neq 0\nonumber\]

for all \(\omega \in \mathbb{R}\) and \(\Delta \in \Delta\) with \(\|\Delta\|_{\infty} \leq 1\). Now using the concept of the structured singular value we arrive at the following condition which is both necessary and sufficient for the Hurwitz stability of the entire family 

\[\mu(M(j \omega))<1\nonumber\]

for all \(\omega \in \mathbb{R}\), where

\[M(j \omega)=\frac{1}{P(j \omega, 0)}\left[\begin{array}{c}
\gamma_{n-1}(j \omega)^{n-1} \\
\gamma_{n-2}(j \omega)^{n-2} \\
\vdots \\
\gamma_{1}(j \omega) \\
\gamma_{0}
\end{array}\right]\left[\begin{array}{lll}
1 & 1 & \ldots 1
\end{array}\right]\nonumber\]

Clearly this is a rank one matrix and by our previous discussion the structured singular value can be computed analytically resulting in the following test

\[\frac{1}{|P(j \omega, 0)|} \sum_{i=1}^{n}\left|\gamma_{n-i}\right||\omega|^{n-i}<1\nonumber\]

for all \(\omega \in \mathbb{R}\).