22.4: Exercises

Exercise \(\PageIndex{1}\)

Suppose you are given the single-input, nth-order system \(x(k + 1) = Ax(k) + bu(k)\), and assume the control \(u\) at every time step is confined to lie in the interval [0, 1]. Assume also that an eigenvalue of \(A\), say \(\lambda_{1}\), is real and nonnegative. Show that the set of states reachable from the origin is confined to one side of a hyperplane through the origin in \(\mathcal{R}^{n}\). (Hint: An eigenvector associated with \(\lambda_{1}\) will help you make the argument.)

[A hyperplane through the origin is an (n - 1)-dimensional subspace defined as the set of vectors \(x\) in \(\mathcal{R}^{n}\) for which \(a^{\prime} x=0\), where \(a\) is some fixed nonzero vector in \(\mathcal{R}^{n}\). Evidently \(a\) is normal to the hyperplane. The two "sides" of the hyperplane, or the two "half-spaces" defined by it, are the sets of \(x\) for which \(a^{\prime} x \leq 0\) and \(a^{\prime} x \geq 0\).]

Exercise \(\PageIndex{2}\)

Given the system

\[x(k+1)=\left(\begin{array}{cc}
a & b \\
0 & c
\end{array}\right) x(k)+\left(\begin{array}{c}
d \\
e
\end{array}\right) u\tag{k}\]

where \(a, b, c, d, e\) are scalars, deduce precisely what condition these coefficients satisfy when the system is not reachable. Draw a block diagram corresponding to the above system and use it to interpret the following special cases in which reachability is lost: (a) e = 0; (b) b = 0 and d = 0; (c) b = 0 and c = a.

Exercise \(\PageIndex{3}\)

(a) Given m-input system \(x(k+1)=A x(k)+B u(k)\), where \(A\) is the Jordan-form matrix

\[A=\left(\begin{array}{lllll}
2 & 1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0 \\
0 & 0 & 2 & 0 & 0 \\
0 & 0 & 0 & 3 & 1 \\
0 & 0 & 0 & 0 & 3
\end{array}\right)\nonumber\]

obtain conditions that are necessary and sufficent for the system to be reachable. (Hint: Your conditions should involve the rows \(b_{i}\) of \(B\). Some form of the modal reachability test will - not surprisingly! - lead to the simplest solution.)

(b) Generalize this reachability result to the case where \(A\) is a general \(n \times n\) Jordan-form matrix.

(c) Given the single-input, reachable system \(x(k + 1) = Ax(k) + bu(k)\), show that there can be only one Jordan block associated with each distinct eigenvalue of \(A\).

Exercise \(\PageIndex{4}\)

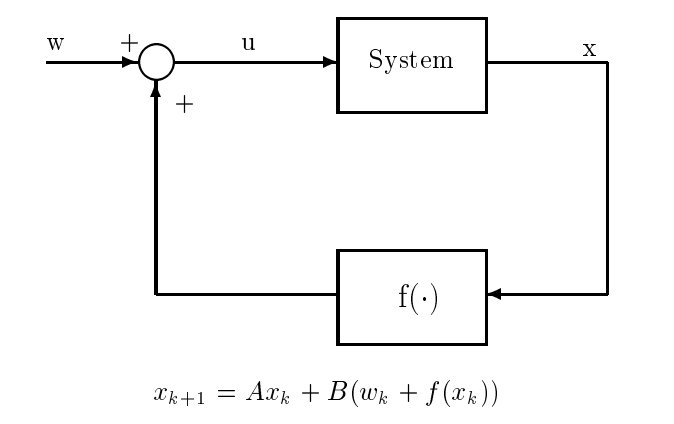
Given the n-dimensional reachable system \(x(k + 1) = Ax(k) + Bu(k)\), suppose that \(u(k)\) is generated according to the nonlinear feedback scheme shown in the figure, where \(u(k) = w(k) + f (x(k))\), with \(f (.)\) being an arbitrary but known function, and \(w(k)\) being the new control input for the closed-loop system.

Show that \(w(k)\) can always be chosen to take the system state from the origin to any specified target state in no more than n steps. You will thereby have proved that reachability is preserved under (even nonlinear) state feedback.

Exercise \(\PageIndex{5}\)

Consider the following linear SISO System, \(\Sigma\):

\[\begin{aligned}
x(k+1) &=A(k) x(k)+B(k) u(k) \\
y(k) &=C(k) x(k)+D(k) u(k)
\end{aligned}\nonumber\]

where \(A(k)=A(k+N) \forall k \geq 0\), similarly for B(k), C(k), and D(k)

(a) Show that \(\Sigma\) is N-Periodic, i.e., for zero initial conditions, show that if y is the output response for some input u, then \(y(k - N)\) is the output response for \(u(k - N)\). Assume for simplicity that \(u(k) = 0\) for \(k < 0\). We want to get a different representation of this system that is easier to work with. To achieve this, we will group together every \(N\) successive inputs starting from \(k = 0\). We will also do the same for the output. To be more precise, we will define a mapping \(L\), called a lifting, such that

\[L:(u(0), u(1), u(2), \ldots, u(k), \ldots) \rightarrow \tilde{u}\nonumber\]

where

\[\tilde{u}=\left(\left(\begin{array}{c}
u(0) \\
u(1) \\
\vdots \\
u(N-1)
\end{array}\right),\left(\begin{array}{c}
u(N) \\
u(N+1) \\
\vdots \\
u(2 N-1)
\end{array}\right), \cdots,\left(\begin{array}{c}
u(k N) \\
u(k N+1) \\
\vdots \\
u((k+1) N-1)
\end{array}\right), \cdots\right)\nonumber\]

Similarly, \(L: y \rightarrow \tilde{y}\)

(b) Show that the system mapping \(\tilde{u}\) to \(\tilde{y}\) is linear time invariant. We will denote this by \(\tilde{\Sigma}\), the lifted system. What are the dimensions of the inputs and outputs. (In other words, by lifting the inputs and outputs, we got rid of the periodicity of the system and obtained a Multi-Input Multi-Output System).

(c) Give a state-space description of the lifted system. (Hint: Choose as a state variable \(\tilde{x}(k)=x(k N)\), i.e., samples of the original state vector. Justify this choice.

(d) Show that the reachable subspace of the lifted system \(\tilde{\Sigma}\) is included in the reachable subspace of the periodic system \(\Sigma\). Show that the converse is true if the periodic system is reachable in \(T\) steps with \(T = rN\) (a multiple of the period).

(e) Is it true that reachability of the periodic system \(\Sigma\) implies reachability of the lifted system \(\tilde{\Sigma}\). Prove or show a counter example.