1.4: An Electro-Mechanical System Model
- Page ID
- 24388
Model of a DC Motor
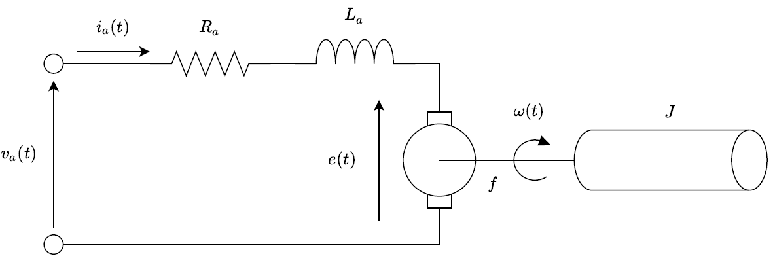
A electro-mechanical system converts electrical energy into mechanical energy or vice versa. A armature-controlled DC motor (Figure 1.4.1) represents such a system, where the input is the armature voltage, \(V_{ a} (t)\), and the output is motor speed, \(\omega (t)\), or angular position \(\theta (t)\).
In order to develop a model of the DC motor, let \(i_{ a} (t)\) denote the armature current, and \(L\) and \(R\) denote the electrical side inductance and the coil resistance. The mechanical side inertia and friction are denoted as \(J\) and \(b\), respectively. Let \(k_{ t}\) denote the torque constant and \(k_{b}\) the motor constant; then, the dynamic equations of the DC motor are given as:
\[L\frac{ d i_{a} (t)}{ d t} +Ri_{a} (t)+k_{ b} \omega (t)=V_{ a} (t) \nonumber \]
\[J\frac{ d \omega (t)}{ d t} +b\omega (t)-k_{ t} i_{ a} (t)=0 \nonumber \]
By using the Laplace transform, these equations are transformed into algebraic equations as:
\[(Ls+R)i_{ a} (s)+k_{ b} \omega (s)=V_{ a} (s) \nonumber \]
\[(Js+b)\omega (s)-k_{ t} i_{ a} (s)=0 \nonumber \]
Motor Transfer Function
In order to obtain an input-output relation for the DC motor, we may solve the first equation for \(i_a(s)\) and substitute in the second equation. Alternatively, we multiply the first equation by \(k_{ t}\), the second equation by \((Ls+R)\), and add them together to obtain:
\[(Ls+R)(Js+b)\omega (s)+k_{ t} k_{ b} \omega (s)=k_{ t} V_{ a} (s) \nonumber \]
Then, the transfer function of the DC motor with voltage input and angular velocity output is derived as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} }{(Ls+R)(Js+b)+k_{ t} k_{ b} } \nonumber \]
The denominator polynomial in the DC motor transfer function typically has real roots, which are reciprocals of the motor time constants \((\tau _{ e} ,\; \tau _ m )\). In terms of the time constants, the DC motor model is described as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /JL}{(s+1/\tau _{ e} )(s+1/\tau _ m )} \nonumber \]
The electrical constant represents the build up of electrical current in the armature circuit, whreas the mechanical constat represents the build up of motor speed in response to the developed motor torque. Further, the slower mechanical time constant dominates the overall motor response to a change in the armature voltage.
The angular position \(\theta \left(s\right)\) of the shaft is obtained by integrating the angular velocity \(\omega (s)\); the transfer function from \(V_a(s)\) to the angular displacement \(\theta \left(s\right)\) is given as:
\[\frac{\theta (s)}{V_{ a} (s)} =\frac{k_{ t} }{s\left[(Ls+R)(Js+b)+k_{ t} k_{ b} \right]} \nonumber \]
A small DC motor has the following parameter values: \(R=1\Omega\), \(L=0.01\,H\), \(J=0.01\; kgm^{2}\), \(b=0.1; \frac{N-s}{rad}\), and \(k_{t} =k_{b} =0.05\); then, the motor transfer function from armature voltage to angular velocity is obtained as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{500}{(s+100)(s+10)+25} =\frac{500}{(s+10.28)(s+99.72)} \nonumber \]
The two motor time constants are given as: \(\tau _{ e} \cong 1\; 0 ms,\; \tau _ m \cong 100\; ms\), where \({\tau }_e\) matches the time constant of an RL circuit (\({\tau }_e=L/R\)) and \({\tau }_m\) matches the time constant of inertial mass in the presence of friction (\({\tau }_m=J/b\)).
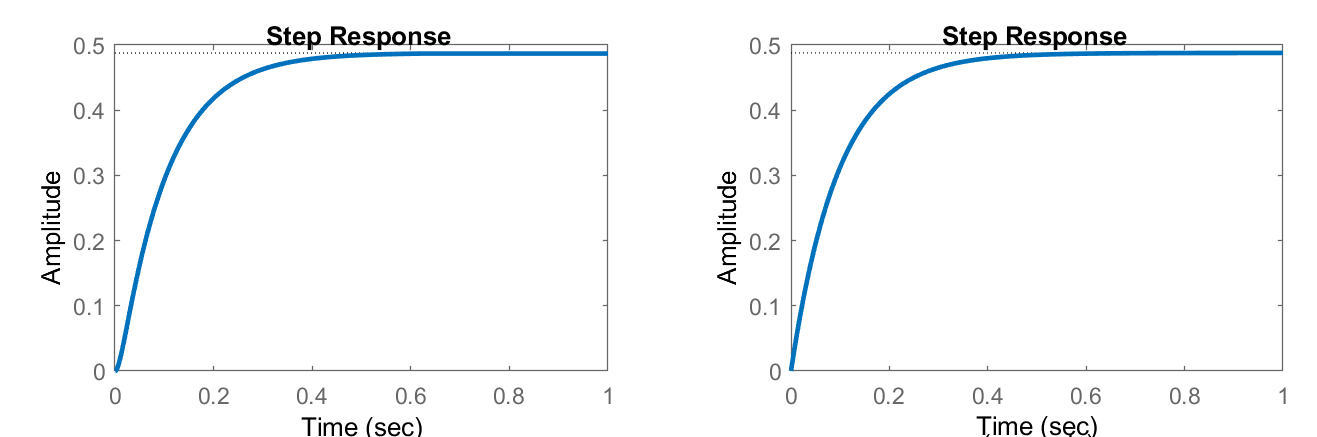
Assuming a unit-step input, \(u(s)=\frac{1}{s}\), is applied to the motor, the motor speed is obtained as:
\[\omega \left(s\right)=\frac{500}{s\left(s+10.28\right)\left(s+99.72\right)}=\frac{0.488}{s}-\frac{0.544}{s+10.28}+\frac{0.056}{s+99.72} \nonumber \]
By applying the inverse Laplace transform, the time-domain output is given as (Figure 13a):
\[\omega \left(t\right)=\left[0.488-0.544e^{-10.28t}+0.056e^{-99.72t}\right]u\left(t\right) \nonumber \]
where \(u\left(t\right)\) denotes a unit-step function. The motor response is plotted in Figure Figure \(\PageIndex{2}\).
Simplified Model of a DC motor
A simplified model of the DC motor is obtained by ignoring the coil inductance (\(L\to 0\)). Then, the electrical side equation is modified as:
\[Ri_a\left(s\right)+k_b\omega \left(s\right)=V_a(s) \nonumber \]
By substituting \(i_a\left(s\right)\) into the torque equation, the mechanical side equation is given as:
\[R(Js+b)\omega (s)+k_{ t} k_{ b} \omega (s)=k_{ t} V_{ a} (s) \nonumber \]
The resulting first-order motor transfer function is given as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /R}{Js+b+k_{ t} k_{ b} /R} \nonumber \]
The first-order model has a single motor time constant \(\left(\tau _ m =\frac{JR}{bR+k_{ t} k_{ b} } \right)\), and is written as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{k_{ t} /JR}{s+1/\tau _m } \nonumber \]
Using the parameter values for a small DC motor (Example 1.4.1), its reduced first-order transfer function is obtained as:
\[\frac{\omega (s)}{V_{ a} (s)} =\frac{5}{s+10.25} \nonumber \]
The resulting motor time constant evaluates as: \(\tau _{m} \cong 97.6\; ms\), which approximates the slower mechanical time constant in the second-order model.
Assuming a unit-step input, the motor response is obtained as:
\[\omega \left(s\right)=\frac{5}{s\left(s+10.25\right)}=\frac{0.488}{s}-\frac{0.488}{s+10.25} \nonumber \]
By applying the inverse Laplace transform, the motor output is given as:\[\omega \left(t\right)=\left[0.488-0.488e^{-10.25t}\right]u\left(t\right) \nonumber \]
The motor response to a unit-step input is plotted in Figure 1.4.2.