10.2: Controllers for Discrete State Variable Models
- Page ID
- 24434
Emulating an Analog Controller
The pole placement controller designed for a continuous-time state variable model can be used with derived sampled-data system model. Successful controller emulation requires a high enough sampling rate that is at least ten times the frequency of the dominant closed-loop poles of the system.
In the following we illustrate the emulation of pole placement controller designed for the DC motor model (Example 8.3.4) for controlling the discrete-time model of the DC motor. The DC motor model is discretized at two different sampling rates for comparison, assuming ZOH at the plant input.
The state and output equations for a DC motor model are given as:
\[\frac{\rm d}{\rm dt} \left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]=\left[\begin{array}{cc} {-100} & {-5} \\ {5} & {-10} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]+\left[\begin{array}{c} {100} \\ {0} \end{array}\right]V_a , \;\;\omega =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_a } \\ {\omega } \end{array}\right]. \nonumber \]
The motor model is discretized at two different sampling rates in MATLAB. The results are:
\[T=0.01s: A_{\rm d} =\left[\begin{array}{cc} {0.367} & {-0.030} \\ {0.030} & {0.904} \end{array}\right],\; \; B_{\rm d} =\left[\begin{array}{c} {0.632} \\ {0.018} \end{array}\right],\; \; C_{\rm d} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]. \nonumber \]
\[T=0.02s: A_{\rm d} =\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right],\; \; B_{\rm d} =\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right],\; \; C_{\rm d} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]. \nonumber \]
For a desired characteristic polynomial: \(\Delta _{\rm des} (s)=s^{2} +150\,s+5000\), a state feedback controller for the continous-time state variable model was obtained as (Example 9.1.1): \(k^{T} =\left[\begin{array}{cc} {0.4} & {7.15} \end{array}\right]\).
We can use the same controller to control the corresponding sample-data system models.
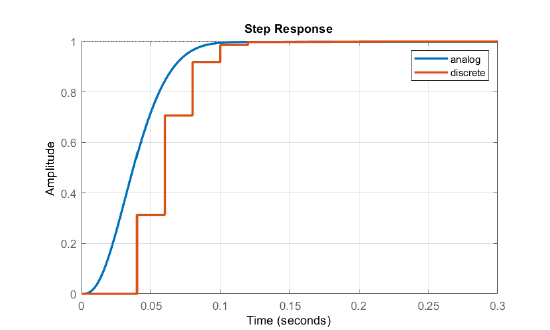
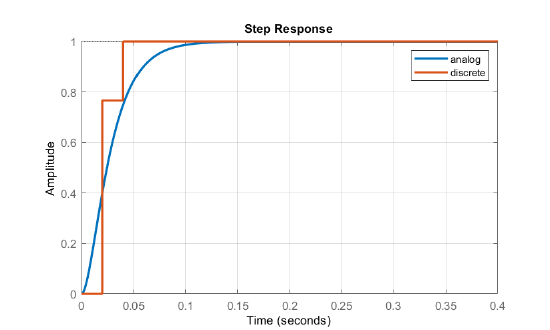
The unit-step response of the closed-loop system is simulated in Figure 10.2.1, where both state variables, \(i_a\left(t\right)\) and \(\omega \left(t\right)\), are plotted.
We observe from the figure that the armature current has a higher overshoot at the lower sampling rate, though both models display similar settling time of about 100 msec.
Pole Placement Design of Digital Controller
Given a discrete state variable model \(\left\{A_{\rm d},\ B_{\rm d}\right\}\), and a desired pulse characteristic polynomial \(\Delta _{\rm des} (z)\), a state feedback controller for the system can be designed using pole placement similar to that of the continuous-time system (Sec. 9.1.1).
Let the discrete-time model of a SISO system be given as:
\[{\bf x}_{k+1} ={\bf A}_{\rm d} {\bf x}_{k} +{\bf b}_{\rm d} u_{k} , \;\; y_{k} ={\bf c}^T {\bf x}_{k} \nonumber \]
A state feedback controller for the discrete state variable model is defined as:
\[u_k=-{\bf k}^T{\bf x}_k+r_k \nonumber \]
where \({\bf k}^{T}\) represents a row vector of constant feedback gains and \(r_k\) is a reference input sequence. The controller gains can be obtained by equating the coefficients of the characteristic polynomial with those of a desired polynomial:
\[\Delta (z)=\left|z{\bf I-A}_{\rm d} \right|=\Delta _{\rm des} (z) \nonumber \]
The \(\Delta _{\rm des} (z)\) above is a Hurwitz polynomial (in \(z\)), with roots inside the unit circle that meet given performance (damping ratio and/or settling time) requirements. Assuming that desired \(s\)-plane root locations are known, the corresponding \(z\)-plane root locations can be obtained from the equivalence: \(z=e^{Ts}\).
Closed-loop System
The closed-loop system model is given as:
\[{\bf x}_{k+1} ={\bf A}_{\rm cl} {\bf x}_{k} +{\bf b}_{\rm d} r_{k} , \;\; y_{k} ={\bf c}^T {\bf x}_{k} \nonumber \]
where \({\bf A}_{\rm cl} =({\bf A}_{\rm d}-{\bf b}_{\rm d}{\bf k}^T)\).
Assuming closed-loop stability, for a constant input \(r_k=r_{\rm ss}\), the steady-state response, \({\bf x}_{\rm ss}\), of the system obeys:
\[{\bf x}_{ss} ={\bf A}_{\rm cl} {\bf x}_{ss} +{\bf b}_{\rm d} r_{ss} ,\;\; y_{\rm ss} ={\bf c}^T {\bf x}_{ss} \nonumber \]
Hence, \(y_{\rm ss}={\bf c}^T\,({\bf A}_{\rm cl}-{\bf I})^{-1}\,{\bf b}_{\rm d}\,r_{\rm ss}\).
The discrete state variable model of a DC motor (\(T=0.02\)s) is given as: \[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\; y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right] \nonumber \]
The desired \(s\)-plane root locations for the model are given as: \(s=-50,\; -100.\)
The corresponding \(z\)-plane roots (\(T=0.02s\)) are obtained as: \(z=e^{-1} ,\; e^{-2}\).
The desired characteristic polynomial is given as: \(\Delta _{\rm des} (z)=z^{2} -0.95z+0.05.\)
The feedback gains \(k^T =[k_{1} ,\; k_{2} ]\), computed using the MATLAB ‘place’ command, are given as: \(k_{1} =0.247,\; k_{2} =4.435.\)
The closed-loop system matrix is given as: \(A_\rm d)= \left[\begin{array}{cc} {-0.080} & {-3.867} \\ {0.025} & {0.583} \end{array}\right]\).
An update rule for implementation of the controller on computer is obtained as: \(u_{k} =-0.247\, i_{k} -4.435\, \omega _{k} .\)
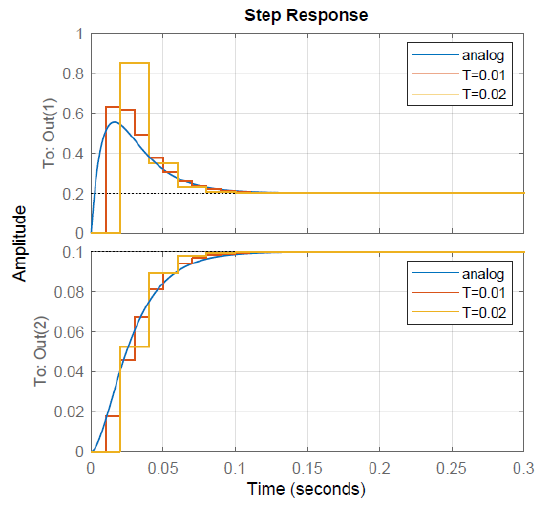
The closed-loop response has steady-state value of \(\omega _{\rm ss}=0.143 \;\rm rad/s\).
The step response of the closed-loop system is plotted in Figure 10.2.2, where the discrete system response was scaled to match the analog system response. The step response of the continuous-time system and that for the emulated controller gains are plotted alongside.
Deadbeat Controller Design
A discrete-time system is called deadbeat if all closed-loop poles are placed at the origin \((z=0)\).
A deadbeat system has the remarkable property that its response reaches steady-state in \(n\)-steps, where \(n\) represents the model dimension.
The desired closed-loop pulse characteristic polynomial is selected as \(\Delta _{\rm des} (z)=z^{n}\).
To design a deadbeat controller, let the closed-loop pulse transfer function be defined as: \[T(z)=\frac{K(z)G(z)}{1+K(z)G(z)} \nonumber \]
The above equation is solved for \(K(z)\) to obtain: \[K(z)=\frac{1}{G(z)} \frac{T(z)}{1-T(z)} \nonumber \]
Let the desired \(T(z)=z^{-n}\); then, the deadbeat controller is given as: \[K(z)=\frac{1}{G(z)(z^{n} -1)} \nonumber \]
Let \(G(s)=\frac{1}{s+1} ;\) then \(G(z)=\frac{1-e^{-T} }{z-e^{-T} }\).
A deadbeat controller for the model is obtained as: \(K(z)=\frac{z-e^{-T} }{(1-e^{-T} )(z-1)}\).
The discrete state variable model of a DC motor for \(T=0.02\; \rm s\) is given as: \[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right] \nonumber \]
The state feedback controller is given as: \(u_{k} =-\left[k_{1} ,\, \, k_{2} \right]x_{k}\).
The closed-loop characteristic polynomial is obtained as: \[\Delta (z)=z^{2} +(0.863k_{1} +0.053k_{2} -0.95)z-0.707k_{1} +0.026k_{2} +0.111 \nonumber \]
For pole placement design, let \(\Delta _{\rm des} (z)=z^{2}\). By equating the polynomial coefficients, the deadbeat controller gains are obtained as: \(k_{1} =0.501,\; k_{2} =9.702\).
The update rule for controller implementation is given as: \[u_{k} =0.501\, \, i_{k} +9.702\, \, \omega _{k} \nonumber \]
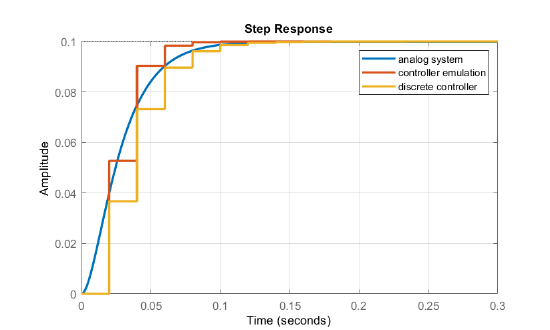
The step response of the deadbeat controller (Figure 10.2.3) settles in two time periods. The response was scaled to match that of the continuous-time system.
An approximate deadbeat design can be performed by choosing distinct closed-loop eigenvalues close to the origin, e.g., \(z=\pm {10}^{-5}\), and using the 'place' command from the MATLAB Control Systems Toolbox.
The feedback gains for the approximate design are obtained as: \(k_{1} =0.509,\; k_{2} =9.702\). The resulting closed-loop system response is still deadbeat.

Feedforward Tracking System Design
A tracking system was previously designed by using feedforward cancelation of the error signal (Section 9.2.1). A similar design can be performed in the case of discrete systems.
Towards this end, let the discrete state variable model be given as: \[{\bf x}_{k+1} ={\bf A}_{\rm d} {\bf x}_{k} +{\bf b}_{\rm d} u_{k} , \;\;y_{k} ={\bf c}^T {\bf x}_{k} \nonumber \]
A tracking controller for the model is defined as: \[u_k=-{\bf k}^T{\bf x}_k+k_rr_k \nonumber \] where \({\bf k}^{T}\) represents a row vector of feedback gains, \(k_r\) is a feedforward gain, and \(r_k\) is a reference input sequence.
Assuming that a pole placement controller for the discrete system has been designed, the closed-loop system is given as: \[{\bf x}_{k+1}=\left({\bf A}_{\rm d}-{\bf b}_{\rm d}{\bf k}^T\right){\bf x}_k+{\bf b}_{\rm d}k_rr_k \nonumber \]
The closed-loop pulse transfer function is obtained as: \[T\left(z\right)={\bf c}^T_{\rm d}{\left(z{\bf I-A}_{\rm d}+{\bf b}_{\rm d}{\bf k}^T\right)}^{-1}{\bf b}_{\rm d}k_r \nonumber \] where \({\bf I}\) denotes an identity matrix. The condition for asymptotic tracking is given as: \[T\left(1\right)={\bf c}^T_{\rm d}{\left({\bf I-A}_{\rm d}+{\bf b}_{\rm d}{\bf k}^T\right)}^{-1}{\bf b}_{\rm d}k_r=1 \nonumber \]
The feedforward gain for error cancelation is obtained as: \(k_r=\frac{1}{T\left(1\right)}\).
The discrete state variable model of a DC motor (\(T=0.02\)s) is given as: \[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right] \nonumber \]
A state feedback controller for the motor model was previously designed as: \(k^T =[k_{1} ,\; k_{2} ]\), where \(k_{1} =0.247,\; k_{2} =4.435.\)
The closed-loop system is defined as: \[T\left(z\right)=\frac{0.367z+0.179}{z^2-0.503z+0.05}k_r \nonumber \]
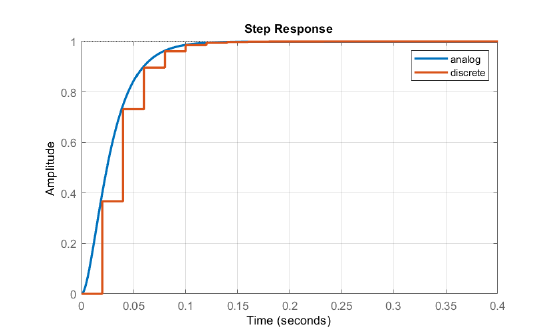
From the asymptotic condition, the feedforward gain is solved as: \(k_r=6.98\).
The step response of the closed-loop system is shown in Figure 10.2.4.
The discrete state variable model of a DC motor (\(T=0.02\)s) is given as:
\[\left[\begin{array}{c} {i_{k+1} } \\ {\omega _{k+1} } \end{array}\right]=\left[\begin{array}{cc} {0.134} & {-0.038} \\ {0.038} & {0.816} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right]+\left[\begin{array}{c} {0.863} \\ {0.053} \end{array}\right]V_{k} , \;\;y_{k} =\left[\begin{array}{cc} {0} & {1} \end{array}\right]\left[\begin{array}{c} {i_{k} } \\ {\omega _{k} } \end{array}\right] \nonumber \]
A dead-beat controller for the motor model was designed as: \(k^T =[k_{1} ,\; k_{2} ]\), where \(k_{1} =0.501,\; k_{2} =9.702\).
The closed-loop system is defined as: \[T\left(z\right)=\frac{0.672z+0.328}{z^2}k_r \nonumber \]
From the asymptotic condition, the feedforward gain is solved as: \(k_r=12.77\).
The step response of the closed-loop system is shown in Figure 10.2.5.
Tracking PI Controller Design
A tracking PI controller for the discrete state variable model is designed similar to the design of continuous-time system (Figure 9.3.1). The tracking PI controller places an integrator in the feedback loop, thus ensuring that the tracking error goes to zero in the steady-state.
In the case of continuous-time system, the tracking PI controller was defined as: \(u=-{\bf k}^{T} {\bf x}+k_{i} \int (r-y)\rm dt\).
Using the forward difference approximation to the integrator, given as: \(v_k=v_{k-1}+Te_k\), an augmented discrete-time system model including the integrator state variable is formed as:
\[\left[\begin{array}{c} {{\bf x}(k+1)} \\ {v(k+1)} \end{array}\right]=\left[\begin{array}{cc} {{\bf A}_{\rm d} } & {\bf 0} \\ {-{\bf c}^T T} & {1} \end{array}\right] \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right]+\left[\begin{array}{c} {{\bf b}_{\rm d} } \\ {0} \end{array}\right]u+\left[\begin{array}{c} {\bf 0} \\ {T} \end{array}\right]r \nonumber \]
The state feedback controller for the augmented system is defined as:
\[u(k)=\left[\begin{array}{cc} {-{\bf k}^T } & {k_ i } \end{array}\right]\, \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right] \nonumber \]
where \(k_ i\) represents the integral gain. With the addition of the above controller, the closed-loop system is described as:
\[\left[\begin{array}{c} {{\bf x}(k+1)} \\ {v(k+1)} \end{array}\right]=\left[\begin{array}{cc} {{\bf A}_{\rm d} -{\bf b}_{\rm d} k^{T} } & {{\bf b}_{\rm d} k_{i} } \\ {-{\bf c}^T T} & {1} \end{array}\right] \left[\begin{array}{c} {{\bf x}(k)} \\ {v(k)} \end{array}\right]+\left[\begin{array}{c} {\bf 0} \\ {T} \end{array}\right]r(k) \nonumber \]
The closed-loop characteristic polynomial of the augmented system is formed as:
\[{\mathit{\Delta}}_a\left(z\right)=\left| \begin{array}{cc} z{\bf I-A}_{\rm d}+{\bf b}_{\rm d}k^T & -{\bf b}_{\rm d}k_i \\ -{\bf c}^T_{\rm d}T & z-1 \end{array} \right| \nonumber \]
where \({\bf I}\) denotes an identity matrix of order \(n\).
Next, we choose a desired characteristic polynomial of \((n+1)\) order, and perform pole placement design for the augmented system. The location of the integrator pole in the \(z\)-plane may be selected keeping in view the desired peformance criteria for the closed-loop system.
The discrete state variable model of a DC motor (\(T=0.02\)s) is given as:
\[\left[ \begin{array}{c} i_{k+1} \\ {\omega }_{k+1} \end{array} \right]=\left[ \begin{array}{cc} 0.134 & -0.038 \\ 0.038 & 0.816 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \end{array} \right]+\left[ \begin{array}{c} 0.863 \\ 0.053 \end{array} \right]V_k,\ \ {\omega }_k=\left[ \begin{array}{cc} 0 & 1 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \end{array} \right] \nonumber \]
The control law for the tracking PI controller is defined as:
\[u_k=-k_1i_k-k_2{\omega }_k+k_iv_k \nonumber \]
where \(v_{k} =v_{k-1} +T(r_{k} -\omega _{k} )\) describes the output of the integrator. The augmented system model for the pole placement design using integral control is given as:
\[\left[ \begin{array}{c} i_{k+1} \\ {\omega }_{k+1} \\ v_{k+1} \end{array} \right]=\left[ \begin{array}{ccc} 0.134 & -0.038 & 0 \\ 0.038 & 0.816 & 0 \\ 0 & -0.02 & 1 \end{array} \right]\left[ \begin{array}{c} i_k \\ {\omega }_k \\ v_k \end{array} \right]+\left[ \begin{array}{c} 0.863 \\ 0.053 \\ 0 \end{array} \right]V_k+\left[ \begin{array}{c} 0 \\ 0 \\ 0.02 \end{array} \right]r_k \nonumber \]
The desired \(z\)-plane pole locations for a desired \(\zeta=0.7\) are selected as: \(z=e^{-1} ,\; e^{-1\pm j1}\).
The controller gains, obtained using the MATLAB ‘place’ command, are given as: \(k_{1} =0.43,k_{2} =15.44,\; k_{i} =-297.79.\)
An update rule for controller implementation on computer is given as:
\[u_k=-0.43i_k-15.44{\omega }_k+297.8v_k \nonumber \]
\[v_k=v_{k-1}+0.02\left(r_k-{\omega }_k\right) \nonumber \]
The step response of the closed-loop system is plotted in Figure 10.2.6. The step response of the continuous-time system (Example 9.1.1) is plotted alongside. The output in both cases attains steady-state value of unity in about 0.12sec.