1.1: Warming Up

To show how to use divide-and-conquer reasoning, we’ll apply it to increasingly complex problems that illustrate its essential features. So we start with an everyday estimate.

What is, roughly, the volume of a dollar bill?

Volumes are hard to estimate. However, we should still make a quick guess. Even an inaccurate guess will help us practice courage and, when we compare the guess with a more accurate estimate, will help us calibrate our internal measuring rods. To urge me on, I often imagine a mugger who holds a knife at my ribs, demanding, “Your guess or your life!” Then I judge it likely that the volume of a dollar bill lies between 0.1 and 10 cubic centimeters.

This range is wide, spanning a factor of 100. In contrast, the dollar bill’s width probably lies between 10 and 20 centimeters—a range of only a factor of 2. The volume range is wider than the width range because we have no equivalent of a ruler for volume; thus, volumes are less familiar than lengths. Fortunately, the volume of the dollar bill is the product of lengths.

\[volume = width \times height \times thickness\]

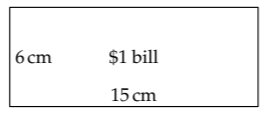
The harder volume estimate becomes three easier length estimates—the benefit of divide-and-conquer reasoning. The width looks like 6 inches, which is roughly 15 centimeters. The height looks like 2 or 3 inches, which is roughly 6 centimeters. But before estimating the thickness, let’s talk about unit systems.

Is it better to use metric or US customary units (such as inches, feet, and miles)?

Your estimates will be more accurate if you use the units most familiar to you. Raised in the United States, I judge lengths more accurately in inches, feet, and miles than in centimeters, meters, or kilometers. However, for calculations requiring multiplication or division—most calculations—I convert the customary units to metric (and often convert back to customary units at the end). But you may be fortunate enough to think in metric. Then you can estimate and calculate in a single unit system.

The third piece of the divide-and-conquer estimate, the thickness, is difficult to judge. A dollar bill is thin—paper thin.

But how thin is “paper thin”?

This thickness is too small to grasp and judge easily. However, a stack of several hundred bills would be graspable. Not having that much cash lying around, I’ll use paper. A ream of paper, which has 500 sheets, is roughly 5 centimeters thick. Thus, one sheet of paper is roughly 0.01 centimeters thick. With this estimate for the thickness, the volume is approximately 1 cubic centimeter:

\[\textrm{volume} \approx \underbrace{15cm}_{\textrm{width}} \times \underbrace{6cm}_{\textrm{height}} \times \underbrace{0.01cm}_{\textrm{thickness}} \approx 1 cm^{3}.\]

Although a more accurate calculation could adjust for the fiber composition of a dollar bill compared to ordinary paper and might consider the roughness of the paper, these details obscure the main result: A dollar bill is 1 cubic centimeter pounded paper thin.

To check this estimate, I folded a dollar bill until my finger strength gave out, getting a roughly cubical packet with sides of approximately 1 centimeter—making a volume of approximately 1 cubic centimeter!

In the preceding analysis, you may have noticed the = and ≈ symbols and their slightly different use. Throughout this book, our goal is insight over accuracy. So we’ll use several kinds of equality symbols to describe the accuracy of a relation and what it omits. Here is a table of the equality symbols, in descending order of completeness and often increasing order of usefulness.

\(equiv\) equality by definition	read as "is defined to be"
= equality	"is equal to"
\(\approx\) equality except for a purely numerical factor near 1	"is approximately equal to"
~ equality except perhaps for a purely numerical factor	"is roughly equal to" or "is comparable to"
\(\alpha\) equality except perhaps for a factor that may have dimension	"is proportional to"

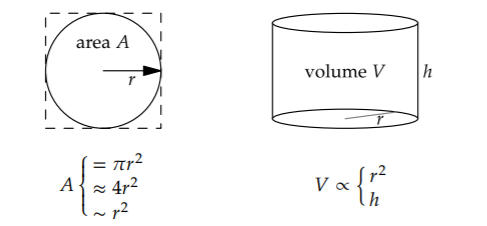
As examples of the kinds of equality, for the circle below, \(A = \pi r^{2}\), and \(A \approx 4r^{2}\), and \(A \sim r^{2}\). For the cylinder, \(V \sim hr^{2}\)

—which implies \(V \propto r^{2}\) and \(V \: \propto \: h\). In the \(V \: \propto \: h\) form, the factor hidden in the \(\propto\) symbol has dimensions of length squared.

Exercise \(\PageIndex{1}\): Weight of a box of books

How heavy is a small moving-box filled with books?

Exercise \(\PageIndex{2}\): Mass of air in your bedroom

Estimate the mass of air in your bedroom.

Exercise \(\PageIndex{3}\): Suitcase of bills

In the movies, and perhaps in reality, cocaine and elections are bought with a suitcase of $100 bills. Estimate the dollar value in such a suitcase.

Exercise \(\PageIndex{4}\): Gold or bills?

As a bank robber sitting in the vault planning your getaway, do you fill your suitcase with gold bars or $100 bills? Assume first that how much you can carry is a fixed weight. Then redo your analysis assuming that how much you can carry is a fixed volume.