2.3: Purpose of Abstraction

The coin game (Section 2.2), like the geometric series (Problem 2.4) or the resistive ladder(Problem 2.8), contained a copy of itself. Noticing this reuse greatly simplified the analysis. Abstraction has a second benefit: giving us a high-level view of a problem or situation. Abstractions then show us structural similarities between seemingly disparate situations.

As an example, let's revisit the geometric mean, introduced in Section 1.6 to make gut estimates. The geometric mean of two nonnegative quantities a and b is defined as

\[\textrm{geometric mean} \equiv \sqrt{ab}\]

This mean is called the geometric mean because it has a pleasing geometric construction. Divide the diameter of a circle into two lengths, a and b, and inscribe a right triangle whose hypotenuse is the diameter. The triangle’s altitude is the geometric mean of a and b.

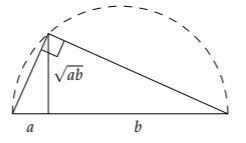
This mean reappears in surprising places, including the beach. When you stand at the shore and look at the horizon, you are seeing a geometric mean. The distance to the horizon is the geometric mean of two important lengths in the problem (Problem 2.9).

For me, its most surprising appearance was in the “Programming and Problem-Solving Seminar” course taught by Donald Knuth [40] (who also created TEX, the typesetting system for this book). The course, taught as a series of two-week problems, helped first-year PhD students transition from undergraduate homework problems to PhD research problems. A homework problem requires perhaps 1 hour. A research problem requires, say 1000 hours: roughly a year of work, allowing for other projects. (A few problems stapled together become a PhD.) In the course, each 2-week module required about 30 hours—approximately the geometric mean of the two endpoints. The modules were just the right length to help us cross the bridge from homework to research.

Exercise \(\PageIndex{1}\): Horizon distance

How far is the horizon when you are standing at the shore? Hint: It’s farther for an adult than for a child.

Exercise \(\PageIndex{2}\): Distance to a ship

Standing at the shore, you see a ship (drawn to scale) with a 10-meter mast sail into the distance and disappear from view. How far away was it when it disappeared?

As further evidence that the geometric mean is a useful abstraction, the idea appears even when there is no geometric construction to produce it, such as in making gut estimates. We used this method in Section 1.6 to estimate the population density and then the population of the United States. Let’s practice by estimating the oil imports of the United States in barrels per year—without the divide-and-conquer reasoning of Section 1.4.

The method requires that the gut supply a lower and an upper bound. My gut reports back that it would feel fairly surprised if the imports were less than 10 million barrels per year. On the upper end, my gut would be fairly surprised if the imports were higher than 1 trillion barrels per year—a barrel is a lot of oil, and a trillion is a large number!

You might wonder how your gut too can come up with such large numbers and how you can have any confidence in them. Admittedly, I have practiced a lot. But you can practice too. The key is the practice effectively. First, have the courage to guess even when you feel anxious about it (I feel this anxiety still, so I practice this courage often). Second, compare your guess to values in which you can place more confidence—for example, to your own more careful estimates or to official values. The comparison helps calibrate your gut (your right brain) to these large magnitudes. You will find a growing and justified confidence in your judgment of magnitude.

My best guess for the amount is the geometric mean of the lower and upper estimates:

\[\sqrt{10 \: million \times 1 \: trillion} \frac{barrels}{year}\]

The result is roughly 3 billion barrels per year—close to the our estimate using divide and conquer and close to the true value. In contrast, the arithmetic mean would have produced an estimate of 500 billion barrels per year, which is far too high.

Exercise \(\PageIndex{1}\): Arithmetic-mean-geometric-mean inequality

Use the geometric construction for the geometric mean to show that the arithmetic mean of a and b (assumed to be nonnegative) is always greater than or equal to their geometric mean. When are the means equal?

Exercise \(\PageIndex{2}\): Weighted geometric mean

A generalization of the arithmetic mean of a and b as (a + b)/2 is to give a and b unequal weights. What is the analogous generalization for a geometric mean? (The weighted geometric mean shows up in Problem 6.29 when you estimate the contact time of a ball bouncing from a table.)