3.2: From Invariant to Symmetry Operation

In the preceding examples, we knew the moves of the game and sought the invariant. In the mouse-eaten chessboard (Section 3.1.2), the moves are putting down a 2 × 1 domino on two adjacent empty squares. The invariant was the difference between empty black and white squares. Often, however, the benefit of invariants lies in the other direction: You know the invariant and seek the moves that preserve it. These moves are called the symmetry operations or simply the symmetries.

We’ll first examine this idea in a familiar situation: converting units (Section 3.2.1). Then we’ll practice it on a sum solved by the three-year-old Carl Friedrich Gauss (Section 3.2.2) and then by finding maxima and minima (Section 3.2.3).

3.2.1 Converting units

We often convert a quantity from one unit system to another—for example, mass from English to metric units or prices from dollars to pounds or euros. A useful physical conversion is writing energy density—energy divided by amount of stuff—in useful units. Let’s start with the reasonable energy unit for a chemical bond, namely the electron volt or eV (Section 2.1). Then a useful unit for energy density is

\[\frac{1eV}{molecule}\]

This energy density is our invariant. As we convert from one unit system to another, our moves have to preserve the energy density.

What are the legal moves—the moves that preserve the energy density?

The legal moves are all ways of multiplying by 1—for example, by

\[\frac{6 \times 10^{23} \: molecules}{1mol} \: \textrm{or} \: \frac{1mol}{6 \times 10^{23} \: molecules}.\]

Either quotient is a form of 1, because 1 mole is defined to be Avogadro’s number of molecules, and Avogadro’s number is 6×10²³. I carefully wrote “1 mol” with the number rather than simply as “mol.” The more explicit form reminds us that “6×10²³ molecules per mole” is shorthand for a quotient of two identical quantities: 6×10²³ molecules and 1 mole.

Multiplying the energy density by the first form of 1 gives

\[\frac{1eV}{\cancel{molecule}} \times \frac{6 \times 10^{23} \cancel{molecules}}{1mol} = \frac{6 \times 10^{23} eV}{mol}.\]

(If we had multiplied by the second form of 1, the units of molecules would have become molecules squared instead of canceling. The strike-through lines help us check that we got the desired units.) The strike-through lines help us check that we got the desired units.) The giant exponent makes this form almost meaningless. To improve it, let's multiply by another form of 1, based on the definition of an electron volt. Two forms of 1 are

\[\frac{1.6 \times 10^{-19}J}{1eV} \textrm{or} \frac{1eV}{1.6 \times 10^{-19}J}.\]

Multiplying by the first form of 1 gives

\[\frac{1\cancel{eV}}{\cancel{molecule}} \times \frac{6 \times 10^{23} \cancel{molecules}}{1mol} \times \frac{1.6 \times 10^{-19}J}{1 \cancel{eV}} \approx \frac{10^{2} kJ}{mol}.\]

(A more exact value is 96 kilojoules per mole.) In the United States, energies related to food are stated in Calories, also known as kilocalories (roughly 4.2 kilojoules). In calorie units, the useful energy-density unit is

\[\frac{96 \cancel{kJ}}{1mol} \times \frac{1kcal}{4.2 \cancel{kJ}} \approx \frac{23 kcal}{mol}.\]

Which form is more meaningful: \(23 \frac{kcal}{mol} \: \textrm{or} \: \frac{23 kcal}{mol}\)?

The forms are mathematically equivalent: You can multiply by 23 before or after dividing by a mole. However, they are not psychologically equivalent. The first form builds the abstraction of kilocalories per mole, and then says, “Here are 23 of them.” In contrast, the second form gives us the energy for 1 mole, a human-sized amount. The second form is more meaningful.

Similarly, the speed of light c is commonly quoted as (approximately)

\[3 \times 10^{8} \frac{m}{s}\]

The psychologically fruitful alternative is

\[c = \frac{3 \times 10^{8} m}{1s}\]

This form suggests that 300 million meters, at least for light, is the same as 1 second. With this idea, you can convert wavelength to frequency (Problem\(\PageIndex{3}\)); with a slight extension, you can convert frequency to energy (Problem \(\PageIndex{4}\)) and energy to temperature (Problem \(\PageIndex{5}\)).

Exercise \(\PageIndex{1}\): Absurd units

By multiplying by suitable forms of 1, convert 1 furlong per fortnight into meters per second.

Exercise \(\PageIndex{2}\): Rainfall units

Rainfall, in nonmetric parts of the world, is sometimes measured in acre feet. By multiplying by suitable forms of 1, convert 1 acre foot to cubic meters. (One square mile is 640 acres.)

Exercise \(\PageIndex{3}\): Converting wavelength to frequency

Convert green-light wavelength, 0.5 micrometers (0.5 μm), to a frequency in cycles per second (hertz or Hz).

Exercise \(\PageIndex{4}\): Converting frequency to energy

Analogously to how you used the speed of light in Problem \(\PageIndex{3}\), use Planck’s constant h to convert the frequency of green light to an energy in joules (J) and in electron volts (eV). This energy is the energy of a green-light photon.

Exercise \(\PageIndex{5}\): Converting energy to temperature

Use Boltzmann’s constant k_B to convert the energy of a green-light photon (Problem \(\PageIndex{4}\)) to a temperature (in kelvin). This temperature, except for a factor of 3, is the surface temperature of the Sun!

Conversion factors need not be numerical. Insight often comes from symbolic factors. Here is an example from fluid flow. As we will derive in Section 5.3.2, the drag coefficient c_d is defined as the dimensionless ratio

\[c_{d} \equiv \frac{F_{drag}}{\frac{1}{2} \rho v^{2} A},\]

where \(\rho\) is the fluid density, v is the speed of the object moving in the fluid, and A is the object’s cross-sectional area. To give this definition and ratio a physical interpretation, multiply it by d/d, where d is the distance that the object travels:

\[c_{d} \equiv \frac{F_{drag}d}{\frac{1}{2} \rho v^{2} Ad},\]

The numerator, \(F_{drag}d\), is the work done or the energy consumed by drag. In the denominator, the product Ad is the volume of fluid displaced by the object, so \(\rho Ad\) is the corresponding mass of fluid. Therefore, the denominator is also

\[\frac{1}{2} \times \textrm{mass of fluid displaced} \times v^{2}\]

The object’s speed v is also approximately the speed given to the displaced fluid (which the object shoved it out of its way). Therefore, the denominator is roughly

\[\frac{1}{2} \times \textrm{mass of fluid displaced} \times (\textrm{speed of displace fluid})^{2}.\]

This expression is the kinetic energy given to the displaced fluid. The drag coefficient is therefore roughly the ratio

\[c_{d} \sim \frac{\textrm{energy consumed by drag}}{\textrm{energy givern to the fluid}}.\]

My tenth-grade chemistry teacher, Mr. McCready, told us that unit conversion was the one idea that we should remember from the entire course. Almost every problem in the chemistry textbook could be solved by unit conversion, which says something about the quality of the book but also about the power of the method.

3.2.2 Gauss’s childhood sum

A classic example of going from the invariant to the symmetry is the following story of the young Carl Friedrich Gauss. Although maybe just a legend, the story is so instructive that it ought to be true. Once upon a time, when Gauss was 3 years old, his schoolteacher, wanting to occupy the students, assigned them to compute the sum

\[S = 1 + 2 + 3 + ... + 100,\]

and sat back to enjoy the break. In a few minutes, Gauss returned with an answer of 5050.

Was Gauss right? If so, how did he compute the sum so quickly?

Gauss saw that the sum—the invariant—is unchanged when the terms are added backward, from highest to lowest:

\[1 + 2 + 3 + ... + 100 = 100 + 99 + 98 + ... + 1.\]

Then he added the two versions of the sum, the original and the reflected:

\[1 + 2 + 3 + .. + 100 = S\]

\[+ 100 + 99 + 98 + ... + 1 = S\]

______________________________

\[101 + 101 + 101 + ... + 101 = 2S\]

In this form, 2S is easy to compute: It contains 100 copies of 101. Therefore, 2S = 100 × 101, and S = 50 × 101 or 5050—as the young Gauss claimed. He made the problem so simple by finding a symmetry: a transformation that preserved the invariant.

Exercise \(\PageIndex{6}\): Number sum

Number sum

Use Gauss’s method to find the sum of the integers between 200 and 300 (inclusive).

Exercise \(\PageIndex{7}\): Symmetry for algebra

Symmetry for algebra

Use symmetry to find the missing coefficients in the expansion of \((a-b)^{3}\):

\[(a-b)^{3} = a^{3} - 3a^{2}b + ? ab^{2} + ? b^{3}\]

Exercise \(\PageIndex{8}\): Integrals

Integrals

Evaluate these definite integrals. Hint: Use symmetry.

(a) \[\int_{-10}^{10} x^{3}e^{-x^{2}}dx\] (b) \[\int_{-\infty}^{\infty} \frac{x^{3}}{1 + 7x^{2} + 18 x^{8}}dx\] and (c) \[\int_{0}^{\infty} \frac{\ln x}{1 + x^{2}} dx.\]

3.2.3 Finding maxima or minima

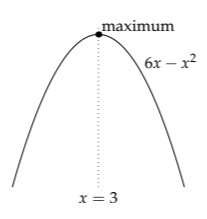
To practice finding the symmetry operation, we’ll find the maximum of the function \(6x - x^{2}\) without using calculus. Calculus is the elephant gun. It can solve many problems, but only after blasting them into the same form (smithereens). Avoiding calculus forces us to use more particular, but more subtle methods—such as symmetry. As Gauss did in summing 1 + 2 + ⋯ + 100, let’s find a symmetry operation that preserves the essential feature of the problem—namely, the location of the maximum.

Symmetry implies moving around an object’s pieces. Fortunately, our function \(6x - x^{2}\) factors into pieces:

\[6x-x^{2} = x(6-x).\]

This form, along with the idea that multiplication is commutative, suggests the symmetry operation. For if the operation just swaps the two factors, replacing \(x(6-x)\) with \((6-x)x\), it does not change the location of the maximum. (A parabola has exactly one maximum or minimum.)

The symmetry operation that makes the swap is

\[x \leftrightarrow 6-x\]

It turns 2 into 4 (and vice versa) and 1 into 5 (and vice versa). The only value unchanged (left invariant) by the symmetry operation is x = 3. Therefore, \(6x-x^{2}\) has its maximum at x = 3.

Geometrically, the symmetry operation reflects the graph of \(6x-x^{2}\) through the line x = 3. By construction, this symmetry operation preserves the location of the maximum. Therefore, the maximum has to lie on the line x = 3.

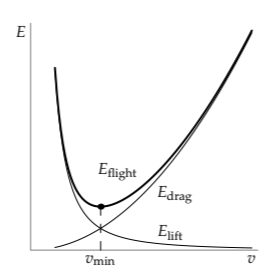
We could have found this maximum in several other ways, so the use of symmetry might seem superfluous or like overkill. However, it warms us up for the following, more complicated use. The energy required to fly has two pieces: generating lift, which requires an energy \(A/v^{2}\), and fighting drag, which requires an energy \(Bv^{2}\). (A and B are constants that we estimate in Sections 3.6.2 and 4.6.1.)

\[E_{flight} = \frac{A}{v^{2}} + Bv^{2}.\]

To minimize fuel consumption, planes choose their cruising speed to minimize E_Flight. More precisely, a cruising speed is selected, and the plane is designed so that this speed minimizes E_Flight.

In terms of the constants A and B, what speed minimizes E_flight?

Like the parabola \(x(6-x)\), this energy has one extremum. For the parabola, the extremum was a maximum; here, it is a minimum. Also similar to the parabola, this energy has two pieces connected by a commutative operation. For the parabola, the operation was multiplication; here, it is addition. Continuing the analogy, if we find a symmetry operation that transposes the two pieces, then the speed preserved by the operation will be the minimum-energy speed.

Finding this symmetry operation is hard to do in one gulp, because it must transpose 1/v² and v² and transpose A and B. These two difficulties suggest that we apply divide-and-conquer reasoning: Find a symmetry operation that transposes 1/v² and v², and then modify so that it also transposes A and B.

To transpose 1/v² and v², the symmetry operation is the following:

\[v \leftrightarrow \frac{1}{v}\]

Now let's restore one of the two constants and modify the symmetry operation so that it transposes \(A/v^{2}\) and \(v^{2}\):

\[v \leftrightarrow \frac{\sqrt{A}}{v}\]

Now let's restore the second constant, B, and find the full symmetry operation that transposes \(A/v^{2}\) and \(Bv^{2}\):

\[\sqrt{B}v \leftrightarrow \frac{\sqrt{A}}{v}\]

Rewriting it as a replacement for v, the symmetry operation becomes

\[v \leftrightarrow \frac{\sqrt{A/B}}{v}\]

This symmetry operation transposes the drag energy and lift energy, leaving the total energy E_Flight unchanged. Solving for the speed preserved by the symmetry operation gives us the minimum-energy speed:

\[v_{min} = (\frac{A}{B})^{1/4}\]

In Section 4.6.1, once we find A and B in terms of the characteristics of the air (its density) and the plane (such as its wingspan), we can estimate the minimum-energy (cruising) speeds of planes and birds.

Problem 3.20 Solving a quadratic equation using symmetry

The equation \(6x-x^{2} + 7 = 0\) has a solution at \(x = -1\). Without using the quadratic formula, find any other solutions.