3.3: Physical Symmetry

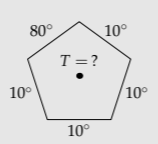
For a physical application of symmetry, imagine a uniform metal sheet, perhaps aluminum foil, cut into the shape of a regular pentagon. Imagine that to the edges are attached heat sources and sinks—big blocks of metal at a fixed temperature—in order to hold the edges at the temperatures marked on the figure. After we wait long enough, the temperature distribution in the pentagon stops changing (comes to equilibrium).

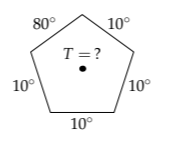
Once the pentagon temperature equilibrates, what is the temperature at its center?

A brute-force, analytic solution is difficult. Heat flow is described by the heat equation, a linear second-order partial-differential equation:

\[\kappa \nabla^{2} = \frac{\delta T}{\delta t}\]

where T is the temperature as a function of position and time, and \(\kappa\) (kappa) is the thermal diffusivity (which we will study in more detail in Chapter 7). But don’t worry: You do not have to understand the equation, only that it is difficult to solve!

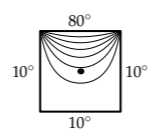
Once the temperature settles down, the time derivative becomes zero, and the equation simplifies to \(\kappa \nabla^{2}T=0\). However, even this simpler equation has solutions only for simple shapes, and the solutions are complicated. For example, the temperature distribution on the simpler square sheet is hardly intuitive (the figure shows contour lines spaced every 10^∘). For a pentagon, the temperature distribution is worse. However, because the pentagon is regular, symmetry might make the solution flow.

What is a useful symmetry operation?

Nature, in the person of the heat equation, does not care about the direction of our coordinate system. Thus, rotating the pentagon about its center does not change the temperature at the center. Therefore, the following five orientations of the pentagon share the same central temperature:

Like Gauss adding the two versions of his sum (Section 3.2.2), stack these sheets mentally and add the temperatures that lie on top of each other to make the temperature profile of a new super sheet (adding the temperatures is valid because the heat equation is linear).

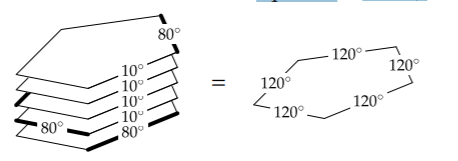
Each super edge contains one 80^∘ edge and four 10^∘ edges, for a temperature of 120^∘. The super sheet is a regular pentagon where all edges are at 120^∘. Therefore, the temperature throughout the sheet is 120^∘—including at the center. Because the symmetry operation has helped us construct a much easier problem, we did not have to solve the heat equation.

One more step tells us the temperature in the center of the original sheet. The symmetry operation rotates the pentagon about its center; when the plates are stacked, the centers align. Each center then contributes one-fifth of the 120^∘ in the center, so the original central temperature is 24^∘.

To highlight the transferable ideas (abstractions), compare the symmetry solutions to Gauss’s sum and to this temperature problem. First, both problems seem complicated. Gauss’s sum has many terms, all different; the pentagon problem seems to require solving a difficult differential equation. Second, both problems contain a symmetry operation. In Gauss’s sum, the symmetry operation reversed the order of the terms; for the pentagon, the symmetry operation rotates it by 72^∘. Finally, the symmetry operation leaves an important quantity unchanged. For Gauss’s problem, this quantity is the sum; for the pentagon, it is the central temperature.

When there is change, look for what does not change. Look for invariants and the corresponding symmetries: the operations that preserve the invariants.

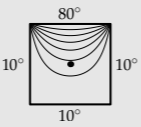
Exercise \(\PageIndex{1}\): Symmetry solution for a square sheet

Here is the contour plot again of the temperature on a square sheet. The contour lines are separated by 10°. Use that information to label the temperature of each contour line. Based on the symmetry reasoning, what should the temperature at the center of the square be? Is this predicted temperature consistent with what is shown in the contour plot?

Exercise \(\PageIndex{2}\): Simulating the heat equation

Using symmetry, we showed that the temperature at the center of the pentagon is the average of the temperatures of the sides. Check the solution by simulating the heat equation with a pentagonal boundary.

Exercise \(\PageIndex{3}\): Shortest bisecting path

What is the shortest path that bisects an equilateral triangle into two equal areas? Here are three examples of bisecting paths:

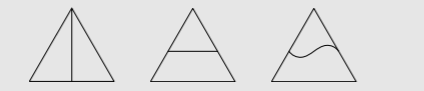
To set your problem-solving gears in motion, first rank these three bisecting paths according to their lengths.