3.6: Lift Using Conservation of Momentum
- Page ID
- 24098
If drag is a drag, our next force, which is the companion to drag, should lift our spirits. Using conservation and box models, we will estimate the power required to generate lift. There are two main cases: hovering flight—for example, a hummingbird—and forward flight. Compared to forward flight, hovering flight has one fewer parameter (there is no forward velocity), so let’s begin with its analysis, for a bird of mass m.
3.6.1 Hovering: Hummingbirds
How much power does a hummingbird require to hover?

Hovering demands power because a hummingbird has weight: The Earth, via the gravitational field, supplies the hummingbird with downward momentum. The Earth therefore loses downward momentum or, equivalently, acquires upward momentum. (Thus, the Earth accelerates upward toward the hummingbird, although very, very slowly.) This flow of momentum can be tracked with a box model. Let’s draw the box around the Earth–hummingbird system and imagine the system as the whole universe. The box contains a fixed (constant) amount of downward momentum, so the gravitational field can transfer downward momentum only within the box. In particular, the field transfers downward momentum from the Earth to the hummingbird. This picture is a fancy way of saying that the Earth exerts a downward force on the hummingbird, but the fancy way shows us what the hovering hummingbird must do to stay aloft.
If the hummingbird keeps this downward momentum, it would accumulate downward speed—and crash to the ground. Fortunately, the box has one more constituent: the fluid (air). The hummingbird gives the downward momentum to the air: It flaps its wings and sends air downward. Lift, like drag, requires a fluid. (The air pushes down on the Earth, returning the downward momentum that the Earth lost via the gravitational field. Thus, the Earth does not accelerate.)
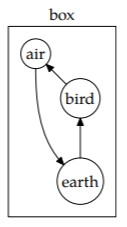
How much power is required to send air downward?
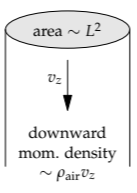
Power is force times speed. The force is the gravitational force mg that the hummingbird is unloading onto the air. Estimating the air’s downward speed vz requires careful thought about the flow of momentum. The air carries the downward momentum supplied to the hummingbird. The momentum supply (a momentum rate or momentum per time) is the force mg: Force is simply momentum per time. Because momentum flux is momentum per time per area,
\[mg = \textrm{momentum flux} \times \textrm{area}\]
When we first studied flux, in Section 3.4.2, we derived that
\[\textrm{flux of stuff} = \textrm{density of stuff} \times \textrm{flow speed}\]
Because our stuff is momentum, this relation takes the particular form
\[\textrm{momentum flux} = \textrm{momentum density} \times \textrm{flow speed}\]
Substituting this momentum flux into \(mg = \textrm{momentum flux} \times \textrm{area}\),
\[mg = \textrm{momentum density} \times \textrm{flow speed} \times textrm{area}\]
Momentum density is momentum \(m_{air}v_{z}\) per volume, so it is \(\rho_{air}v_{z}\). The flow speed is vz. Thus,
\[mg = \rho_{air}v_{z} \times v_{z} \times area = \rho_{air}v^{2}_{z} \times area.\]
To complete this equation, so that it gives us the downward velocity vz, we need to estimate the area. It is the area over which the hummingbird directs air downward. It is roughly L2, where L is the wingspan (wingtip to wingtip). Even though the wings do not fill that entire area, the relevant area is still L2, because the wings disturb air in a region whose size is comparable to their longest dimension. (For this reason, high-efficiency planes, such as gliders, have very long wings.)
Using L2 as the estimate for the area, we get
\[mg \sim \rho_{air}v^{2}_{z}L^{2},\]
so the downward velocity is
\[v_{z} \sim \sqrt{\frac{mg}{\rho_{air}L^{2}}}.\]
With this downward velocity and with the downward force mg, the power P (not to be confused with momentum!) is
\[P = Fv_{z} \sim mg \sqrt{\frac{mg}{\rho_{air}L^{2}}}.\]
Let’s estimate this power for an actual hummingbird: the Calliope hummingbird, the smallest bird in North America. Its two relevant characteristics are the following:
\[\textrm{wingspan} L \approx 11cm,\]
\[\textrm{mass} m \approx 2.5 g.\]
As the first step in estimating the hovering power, we’ll estimate the downward air speed using our formula for vz. The result is that, to stay aloft, the hummingbird sends air downward at roughly 1.3 meters per second:
\[v_{z} \sim (\frac{\overbrace{2.5 \times 10^{-2} N}^{mg}}{\underbrace{1.2 \textrm{kg m}^{-3}}_{\rho_{air}} \times \underbrace{1.2 \times 10^{-2} m^{2}}_{L^{2}}})^{1/2} \approx 1.3 \textrm{m s}^{-1}.\]
The resulting power consumption is roughly 30 milliwatts:
\[P \sim \underbrace{2.5 \times 10^{-2} \textrm{ N}}_{mg} \times \underbrace{1.3 \textrm{m s}^{-1}}_{v_{z}} \approx \underbrace{3 \times 10^{-2} \textrm{W}}_{30 mW}.\]
(Because animal metabolism, like a car engine, is only about 25 percent efficient, the hummingbird needs to eat food at a rate corresponding to 120 milliwatts.)
This power seems small: Even an (incandescent) flashlight bulb, for example, requires a few watts. However, as a power per mass, it looks more significant:
\[\frac{P}{m} \sim \frac{3 \times 10^{-2} W}{2.5 \times 10^{-3} kg} \approx 10 \frac{W}{kg}\]
In comparison, the world-champion cyclist Lance Armstrong, with one of the highest human power outputs, was measured to have a power output of 7 watts per kilogram (Section 1.7.2). However, for a chemically unenhanced world-class athlete, 5 watts per kilogram is a more typical value. According to our estimates, hummingbird muscles should be twice as powerful as this world-class human value! Even for a small bird, hovering is hard work.
Exercise \(\PageIndex{1}\): Fueling hovering
How much nectar must a hummingbird drink, as a fraction of its body mass, in order to hover for its working day (roughly 8 hours)? By mass, nectar is roughly 50 percent sugar.
Exercise \(\PageIndex{2}\): Human hovering
How much power would a person have to put out in order to hover by flapping his or her arms?
3.6.2 Lift in forward flight
Now that we understand the fundamental mechanism of lift—discarding downward momentum by giving it to the air—we are ready to study forward flight: the flight of a migrating bird or of a plane. Forward flight is more complicated than hovering because forward flight has two velocities: the plane’s forward velocity v and the downward component vz of the air’s velocity after passing around the wing. In forward flight, vz depends not only on the plane’s weight and wingspan, but also on the plane’s forward velocity.

To stay aloft, the plane, like the hummingbird, must deflect air downward.

The wing does this magic using complicated fluid mechanics, but we need not investigate it. All the gymnastics are hidden in the box. We need just the downward velocity vz required to keep the plane aloft, and the power required to give the air that much downward velocity. The power is, as with hovering, mgvz. However, the downward velocity vz is not the same as in hovering.
It is determined by a slightly different momentum-flow diagram. It shows the air flow before and after it meets the wing.
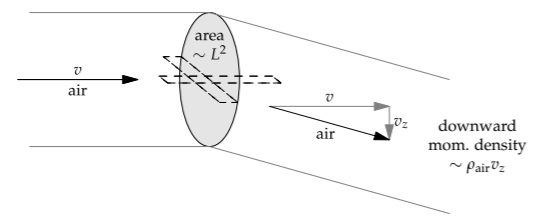
Before the air reaches the wing (the left tube), the air has zero downward momentum. As in the analysis of hovering flight, the Earth supplies downward momentum to the plane, which passes it onto the air. This downward momentum is carried away by the air after the wing (the right tube).
As with any flux, the rate of transfer of downward momentum is
\[\textrm{flux of downward momentum} \times \textrm{area}\]
As in the analysis of the hummingbird, this rate must be mg, so that the plane stays aloft. The first factor, the flux of downward momentum, is
\[\textrm{density of downward momentum} \times \textrm{flow speed}\]
Therefore,
\[mg = \textrm{density of downward momentum} \times \textrm{flow speed} \times textrm{area}\]
As in the analysis of hovering, the density of downward momentum is \(\rho v_{z}\).
In contrast to the analysis of hovering, where the stuff (downward momentum) is carried by the air moving downward, here the stuff is carried by air moving to the right. Thus, where the flow speed in hovering was the downward air speed vz, in forward flight the flow speed is the forward velocity v.
As in the analysis of hovering, the relevant area is the squared wingspan L2, because the wings alterthe airflow over a distance comparable to their longest dimension, which is their wingspan. You can see this effect in a NASA photograph of an airplane flying through a cloud of smoke. The giant swirl, known as the wake vortex, has a diameter comparable to the plane’s wingspan. Large planes can generate vortices that flip over small planes. Thus, when coming in forlanding, planes must maintain enough separation to give these vortices time to dissipate.

With these estimates, the equation for vz becomes
\[\underbrace{mg}_{\textrm{transfer rate}} \sim \underbrace{\rho_{air}v_{z}}_{\textrm{downward-momentum density}} \times \underbrace{v}_{\textrm{flow speed}} \times \underbrace{L^{2}}_{\textrm{area}}.\]
Now we can solve for the downward air speed:
\[v_{z} \sim \frac{mg}{\rho_{air}vL^{2}}.\]
Now we can estimate the power required to generate lift in forward flight:
\[P= \underbrace{\textrm{force}}_{mg} \times \underbrace{\textrm{velocity}}_{v_{z}} \sim mg \times \frac{mg}{\rho_{air} vL^{2}} = \frac{(mg)^{2}}{\rho_{air}vL^{2}}.\]
Here is a comparison of hovering and forward flight.
| hovering | forward flight | |
| deflection area | \(L^{2}\) | \(L^{2}\) |
| downward-momentum density | \(\rho_{air}v_{z}\) | \(rho_{air}v_{z}\) |
| flow speed | \(v_{z}\) | \(v\) |
| downward-momentum flux | \(\rho_{air}v_{z}^{2}\) | \(\rho_{air}v_{z}v\) |
| downward-momentum flow mg | \(\rho_{air}v^{2}_{z}L^{2}\) | \(rho_{air}v_{z}vL^{2}\) |
| downward velocity vz | \(\sqrt{mg/\rho_{air}L^{2}}\) | \(mg/\rho_{air}vL^{2}\) |
| power to generate lift (mgvz) | \(mg\sqrt{mg/\rho_{air}L^{2}}\) | \((mg)^{2}/\rho_{air}vL^{2}\) |
In contrast to hovering, in forward flight the power contains the forward velocity in the denominator—a location that would produce nonsense for hovering, where the forward velocity is zero.
As we did for hovering flight using the Calliope hummingbird, let’s apply our knowledge of forward flight to an actual object. The object will be a Boeing 747-400 jumbo jet, and we will estimate the power that it requires in order to take off. A 747 has a wingspan L of approximately 60 meters, and a maximum takeoff mass m of approximately 4×105 kilograms (400 tons).
We’ll estimate the power in two steps: the weight mg and then the downward air speed vz. The weight is the easy step: It is just 4 × 106 newtons. The downward air speed vz is \(mg/\rho_{air}vL^{2}\). The only unknown quantity is the takeoff speed v. You can estimate it by estimating the plane’s acceleration a while taxiing on the runway and by estimating the duration of the acceleration. When I last flew on a 747, I measured the acceleration by suspending my key chain from a string and estimating the angle \(theta\) that it made with vertical (perpendicular to the ground). Then tan \(theta\) = a/g. For small \(\theta\), the relation simplifies to \(a/g \approx \theta\). I found \(\theta \approx 0.2\), so the acceleration was about 0.2g or 2 meters per second per second. This acceleration lasted for about 40 seconds, giving a takeoff speed of \(v \approx 80\) meters per second (180 miles per hour).
The resulting downward speed vz is roughly 12 meters per second:
\[v_{z} \sim \frac{\overbrace{4 \times 10^{6} \textrm{N}}^{mg}}{\underbrace{1.2 \textrm{kg m}^{-3}}_{\rho_{air}} \times \underbrace{80 \textrm{ m s}^{-1}}_{v} \times \underbrace{3.6 \times 10^{3} \textrm{ m}^{2}}_{L^{2}}} \approx 12 \textrm{ m s}^{-1}.\]
Then the power required to generate lift is roughly 50 megawatts:
\[P \sim mgv_{z} \approx 4 \times 10^{6} N \times 12 ms^{-1} \approx 5 \times 10^{7} W.\]
Let’s see whether these estimates are reasonable. According to the plane’s technical documentation, the 747-400’s four engines together can provide roughly 1 mega-newton of thrust. This thrust can accelerate the plane, with a mass of 4×105 kilograms, at 2.5 meters per second. This value is in good agreement with my estimate of 2 meters per second, made by suspending a key chain from a string and turning it into a plumb line.
As another check: At takeoff, when v is roughly 80 meters per second, the meganewton of thrust corresponds to a power output Fv of 80 megawatts. This output is comparable to our estimate of 50 megawatts for the power to lift the plane off the ground. After liftoff, the engines use some of their power to lift the plane and some to accelerate the plane, because the plane still needs to reach its cruising speed of 250 meters per second.
Symmetry and conservation make even fluid dynamics tractable.


