5.2: One Dimensionless Group
- Page ID
- 24108
The most frequent use of dimensional analysis involves one independent dimensionless group—for example, ar/v2 in our analysis of circular acceleration (Section 5.1.1). Let’s look at this kind of case more closely, which has lessons for more complicated problems.
5.2.1 Universal constants
What we will find is that dimensional analysis reduces complexity by generating results with wide application. That is, in the general form
\[\textrm{independent dimensionless group} = \textrm{dimensionless constant,}\]
the dimensionless constant is universal. Let’s see what universal means through an example—the analysis of a small-amplitude pendulum. So, imagine releasing a pendulum from a small angle \(\theta_{0}\).
What is its period of oscillation?
The first step in dimensional analysis is to list the relevant quantities. The list begins with the goal quantity--here, the period T. It depends on gravity g, the string length l, perhaps the mass m of the bob, and perhaps the amplitude \(\theta_{0}\). Fortunately, when the amplitude is small, as it is here, then the amplitude turns out not to matter, so we won't list it.
| T | T | period |
| g | LT-2 | gravity |
| l | L | string length |
| m | M | mass of bob |
What are the dimensionless groups?
These four quantities contain three independent dimensions (M, L, and T). By the Buckingham Pi theorem (Section 5.1.2), they produce one independent dimensionless group. This group cannot contain m, because m is the only quantity with dimensions of mass. A simple dimensionless group is gT2/l. However, because our eventual goal is the period T, let's make a dimensionless group proportional to T itself rather than to T2 . This group is \(T \sqrt{g/l}\). Then the most general dimensionless statement is
\[T\sqrt{\frac{g}{l}}=C,\]
where C is a dimensionless constant. Even though its value is, for the moment, unknown, it is universal. The same constant applies to a pendulum with a shorter string or, perhaps more surprisingly, to a pendulum on Mars, with its different gravitational strength. If we find the constant for one pendulum on one planet, we know it for all pendulums on all planets.
There are at least three ways to find C. The first is to solve the pendulum differential equation—which is hard work. The second approach is to solve a cleverly designed simpler problem (Problem 3.4). Although the approach is clever, it is not as general as the third method.
The third method is to measure C with a home experiment! For that purpose, I turned my key ring into a pendulum by hanging it from a string. The string was roughly twice the length of American letter paper (thus, 2 × 11 inches) and the period was roughly 1.5 seconds. Therefore,
\[C=T\sqrt{\frac{g}{l}} \approx 1.5s \times \sqrt{\frac{32 ft s^{-2}}{2ft}} = 6.\]

Would the constant be different in a modern system of units?
In metric units, g ≈ 9.8 meters per second per second, l ≈ 0.6 meters, and C is, within calculation inaccuracies, still 6:
\[C \approx 1.5s \times \sqrt{\frac{9.8m/s^{2}}{0.6m}} \approx 6\]
The system of units does not matter—which is the reason for using dimensionless groups: They are invariant under a change of units. Even so, an explicit 6 probably would not appear if we solved the pendulum differential equation honestly. But a more precise measurement of C might suggest a closed form for this dimensionless constant.
The pendulum length, from the knot where I hold it to the center of the key ring is 0.65 meters (slightly longer than the rough estimate of 0.6 meters). Meanwhile, 10 periods took 15.97 seconds. Then C is close to 6.20:
\[C \approx 1.597 s \times \sqrt{\frac{9.8 m s^{-2}}{0.65m}} \approx 6.20.\]
What dimensionless numbers could produce 6.20?
This value is close to 2π, which is approximately 6.28. That guess feels like a leap, but have courage. The guess is plausible once we remember that pendulums oscillate and oscillations often involve 2π, or that we are asking for the period rather than the angular frequency, a choice that often introduces a 2π (as in Problem 5.11(d)). The resulting period T is
\[T = C \sqrt{\frac{l}{g}} = 2 \pi \sqrt{\frac{l}{g}}.\]
(For a physical explanation of the 2π, try Problem 3.4.)
This example shows how dimensional analysis, a mathematical approach, sits between two physical approaches. First we used our physical knowledge to list the relevant quantities. Then we reduced the space of possible relations by using dimensional analysis. Finally, to find the universal constant C, which dimensional analysis could not tell us, we again used physical knowledge (a home experiment).
Exercise \(\PageIndex{1}\): Your own measurement
Make your own pendulum and measure the universal constant \(T \sqrt{g/l}.\)
Exercise \(\PageIndex{2}\): Period of a spring-mass system
Use dimensional analysis to find, except for a dimensionless constant, the period T of a spring–mass system with spring constant k, mass m, and amplitude x0. Find the dimensionless constant in the most general dimensionless statement
\(\textrm{group proportional to} T = \textrm{dimensionless constant}\)
Exercise \(\PageIndex{3}\): Speed of waves in shallow water
In shallow water, where the wavelength is much larger than the depth, waves driven by gravity travel at a speed that could depend on gravity g, the water depth h, and the density of water \(\rho\).
a. Find the independent dimensionless group proportional to v2, where v is the wave speed. Compare this group to the Froude number, the dimensionless ratio that we introduced to study walking (Section 5.1.1).
b. What therefore is the scaling exponent \(\beta\) in the scaling relation \(v \: \propto \: h^{\beta}\)? Test your prediction by measuring v(1cm) and v(4cm). To make the measurement, fill a baking dish with water and excite a sloshing wave by slightly lifting and quickly setting down one end of the dish.

c. Using your data, estimate the universal (dimensionless) constant in the relation
\[\textrm{dimensionless group from part (a)} = \textrm{dimensionless constant.}\]
d. Predict the speed of tidal waves, which are (shallow-water!) waves created by underwater earthquakes. How long does a tidal wave take to cross an ocean?
5.2.2 Atomic blast energy
Problems with only one dimensionless group need not be simple or easy to by other methods. A classic example is finding the energy released by the first atomic bomb, detonated in the New Mexico desert in 1945. The blast energy, or yield, was top secret. Yet declassified photographs of the blast, because they had a scale bar, provided data on the radius of the fireball at several times after the explosion. The data must have seemed innocuous enough to release.
| t (ms) | R (m) |
| 3.26 | 59.0 |
| 4.61 | 67.3 |
| 15.0 | 106.5 |
| 62.0 | 185.0 |
But from these data, G. I. Taylor of Cambridge University predicted the yield [44]. The analysis, like many calculations in fluid mechanics, is long and complicated. We’ll instead use dimensional analysis to find the relation between the blast radius R, the time t since the blast, the blast energy E, and the air density \(\rho\). Then we’ll use the R(t) data to predict E.
These four quantities contain three independent dimensions. Thus, they produce one independent dimensionless group. To find it, let's eliminate one dimension at a time. Here, a bit of luck simplifies the process, because we have dimensions that are easy to eliminate.
| E | ML2T-2 | blast energy |
| R | L | blast radius |
| t | T | time since blast |
| \(rho_{air}\) | ML-3 | air density |
Do any dimensions occur in only one or two quantities?
Yes: Mass occurs in E as M1 and in \(\rho_{air}\) also as M1; time appears in E as T−2 and in t as T1. Therefore, to eliminate mass, the dimensionless group must contain E/\(\rho_{air}\). To eliminate time, the dimensionless group must contain Et2. Thus, Et2/\(\rho_{air}\) eliminates mass and time. Because it has dimensions of L5, the only way to remove these dimensions without introducing any powers of time or mass is to divide by R 5. The result, Et2/\(\rho_{air}R^{5}\), is an independent dimensionless group. It is also the only dimensionless group proportional to our goal, the blast energy E.
With only one dimensionless group, the most general dimensionless statement about the blast energy is
\[\frac{Et^{2}}{\rho_{air}R^{5}} \sim 1\]
For a particular explosion, E is fixed (although unknown), as is \(\rho_{air}\). Therefore, these quantities drop out of the corresponding scaling relation, which becomes \(t^{2} \: \propto \: R^{5}\) or \(R \: \propto \: t^{2/5}\). On log–log axes, the data on the blast radius should fall along a line of slope 2/5—as they almost exactly do:
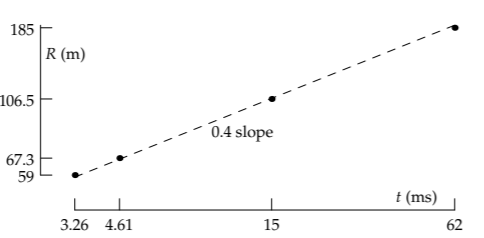
With the dimensional analysis result \(Et^{2}/\rho_{air}R^{5} \sim 1\), each point predicts a blast energy according to \(E \sim \rho_{air}R^{5}/t^{2}/\) Using 1 kilogram per cubic meter for \(\rho_{air}\), the E estimates lie between 5.6 and 6.7 x 1013 joules. Unfortunately for judging the accuracy of the estimate, joules are an unfamiliar unit for the energy of a bomb blast. The familiar unit is tons of TNT.
What is the predicted blast energy as a mass of TNT?
One gram of TNT releases 1 kilocalorie or roughly 4 kilojoules. It contains only one-fourth the energy density of sugar, but the energy is released much more rapidly! One kiloton is 109 grams, which release 4× 1012 joules. Our predicted yield of 6×1013 joules is thus roughly 15 kilotons of TNT.
Just for fun, if we reestimate the yield using a more accurate air density of 1.2 kilograms per cubic meter, the blast energy would be 18 kilotons. This result is shockingly accurate considering the number of approximations it contains: The classified yield was 20 kilotons. (The missing universal constant for shock-wave explosions must be very close to 1.)
Dimensional analysis is powerful!


