6.2: Rounding on a logarithmic scale

Just as driving to visit a next-door neighbor atrophies our muscles and ability to move around the physical world, asking calculators to do simple arithmetic dulls our ability to navigate the quantitative world. We never develop an innate sense of sizes and scales in the world. The antidote is to do the computations ourselves, but approximately—by placing quantities on a logarithmic scale and rounding them to the nearest convenient value.

6.2.1 Rounding to the nearest power of ten

The simplest method of rounding is to round every number to the nearest power of ten. That simplification turns most calculations into adding and subtracting integer exponents (the exceptions come from roots, which produce fractional exponents). Here, “nearest” is judged on a logarithmic scale, where distance is measured not with differences but with ratios or factors. For example, 50—although closer to 10 than to 100 on a linear scale—is a factor of 5 greater than 10 but only a factor of 2 smaller than 100. Therefore, 50 is closer to 100 than to 10 and would get rounded to 100.

As practice, let’s estimate the number of minutes in a day:

\[1 day \times \frac{24 hours}{day} \times \frac{60 minutes}{hour} = 24 \times 60 minutes.\]

Now we round each factor to the nearest power of 10. Because 24 is only a factor of 2.4 away from 10, but more than a factor of 4 away from 100, it gets rounded to 10:

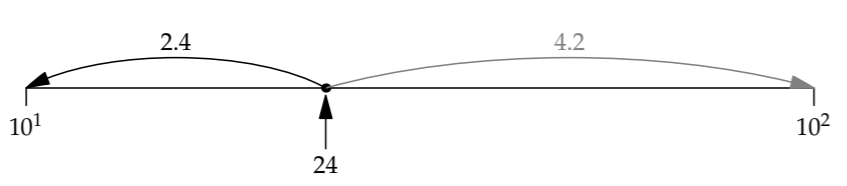
In contrast, 60 is closer to 100 than to 10:

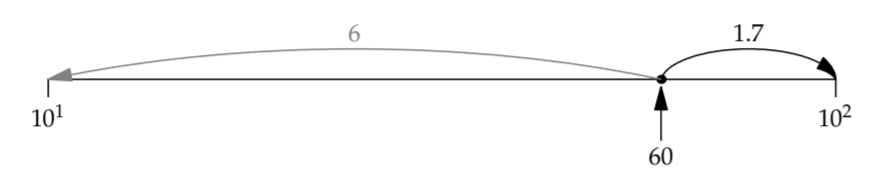
With these approximations, 1 day is approximately 1000 minutes:

\[1 \: day \frac{\overbrace{10}^{from \: 24} hours}{day} \times \frac{\overbrace{100}^{from \: 60} minutes}{hour} = 1000 \: minutes.\]

The exact value is 1440 minutes, so the estimate is only 30 percent too small. This error is a reasonable tradeoff to gain a method that requires almost no effort—who needs a calculator to multiply 10 by 100? Furthermore, the accuracy is enough for many calculations, where insight is needed more than accuracy.

Problem 6.1: Rounding to the nearest power of ten

Round these numbers to the nearest power of ten: 200, 0.53, 0.03, and 7.9.

Problem 6.2: Boundary between rounding up or down?

We saw that 60 rounded up to 100 but that 24 rounded down to 10. What number is just at the boundary between rounding down to 10 and rounding up to 100?

Problem 6.3: Using rounding to the nearest power of ten

Round the numbers to the nearest power of ten and thereby estimate the products: (a) 27 × 50, (b) 432 × 12, and (c) 3.04 × 5.3.

Problem 6.4: Calculating the bending of light

In Section 5.3.1, we used dimensional analysis to show that the Earth could bend starlight by approximately the angle

\[\theta \sim \frac{\overbrace{6.7 \times 10^{-11} kg^{-1} m^{3}s^{-2}}^{G} \times \overbrace{6 \times 10^{24} kg}^{m_{Earth}}}{\underbrace{6.4 \times 10^{6}m}_{R_{Earth}} \times \underbrace{10^{17} m^{2} s^{-2}}_{c^{2}}}.\]

Round each factor to the nearest power of ten in order to estimate the bending angle mentally. How long did making the estimate take?

6.2.2 Rounding to the nearest half power of ten

Rounding to the nearest power of ten gives a quick, preliminary estimate. When it is too approximate, we just round more precisely. The next increase in accuracy is to round to the nearest half power of ten.

As an illustration, let’s estimate the number of seconds in a year. The numerical calculation (without the units) is 365 × 24 × 3600. Now we round each factor by replacing it with a number of the form \(10^{\beta}\). In the previous method, where we rounded to the nearest power of ten, \(\beta\) was an integer. Now \(\beta\) can also be a half-integer (for example, 2.5).

What is a half power of ten numerically?

Two half powers of ten multiply to make 10, so each half power is \(\sqrt{10}\), or slightly more than 3 (as you found in Problem 6.2). When you need more precision, a half power of ten is 3.2 or 3.16, although that much precision is rarely needed.

In rounding the calculation for the number of seconds, 365 becomes 10^2.5, and, as diagrammed below, 3600 becomes 10^3.5:

The remaining factor is 24. It is closer to 10^1.5 (roughly 30) than to 10¹:

Thus, we replace 24 by 10^1.5. Then the calculation simplifies to

\[\underbrace{10^{2.5}}_{365} \times \underbrace{10^{1.5}}_{24} \times \underbrace{10^{3.5}}_{3600}.\]

Now just add the powers of ten:

\[10^{2.5} \times 10^{1.5} \times 10^{3.5} = 10^{7.5}.\]

Because the 0.5 in the exponent 7.5 contributes a factor of 3, there are about 3×10⁷ seconds in a year. I remember this value as \(\pi \times 10^{7}\), which is accurate to 0.5 percent.

Problem 6.5: Earth's orbital speed

Using the estimate of \(\pi \times 10^{7}\) seconds in a year, estimate the Earth’s orbital speed around the Sun. Don’t use a calculator! (The Earth–Sun distance, 1.5×10¹¹ meters, is worth memorizing.)

Problem 6.6: Where does the \(\pi\) come from?

True or false: The \(\pi\) in \(\pi \times 10^{7}\) seconds per year arises because the Earth orbits the Sun in a circle, and a circle has \(\pi\) in its circumference.

Problem 6.7: Only approximately pi

True or false: The \(\pi\) in \(\pi \times 10^{7}\) seconds per year is not exact because the Earth orbits in a slightly noncircular ellipse.

Problem 6.8: Estimating geometric means

In Section 2.3, I talked to my gut to estimate the US annual oil imports. That discussion resulted in the geometric-mean estimate

\[\sqrt{10 \: million \times 1 \: trillion} \textrm{ barrels per year.}\]

Estimate the square root by placing the two quantities 10 million and 1 trillion on a logarithmic scale and finding their midpoint