6.6: Summary and further problems

Last updated
Save as PDF

Page ID: 24119

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lumping is our first tool for discarding complexity with loss of information. By doing so, it simplifies complicated problems where our previous set of tools could not. Curves become straight lines, calculus becomes algebra, and even quantum mechanics becomes comprehensible.

Problem 6.35: Precession of the equinoxes

Because the Earth is oblate (Problem 5.46), and thus has a bit of fat near the equator, and because its rotation axis is tilted relative to the Earth’s orbital plane, the Sun and the Moon each exert a slight torque on the Earth. This torque slowly rotates (precesses) the Earth’s axis of rotation (so the north star will not always be the north star)

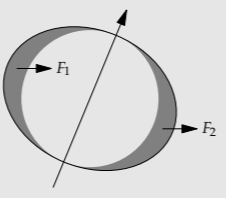
a. Explain why F₁ and F₂, the gravitational forces on the two bulges, are almost exactly equal in direction but not equal in magnitude.

b. Use lumping to find the scaling exponents x and y in

\[\textrm{torque} \propto m^{x} l^{y},\]

where m is the mass of the object (either the Sun or Moon) and l is its distance from the Earth. Then estimate the ratio

\[\frac{\textrm{torque from the Sun}}{\textrm{torque from the Moon}}.\]

c. By including the constants of proportionality, estimate the total torque and the precession rate.

Problem 6.36: Graph lumping in reverse

In a constant-temperature (isothermal) atmosphere, which isn’t a terrible approximation to the actual atmosphere, the air density falls exponentially with height:

\[\rho = \rho_{0} e^{-z/H}.\]

where z is the height above sea level, \(\rho_{0}\) is the density at sea level, and H is the scale height of the atmosphere. We estimated H in Section 5.4.1 using dimensional analysis; in this problem, you’ll estimate it by using lumping in reverse.

a. Sketch \(\rho (z)\) versus z as given above. On the same graph, sketch a lumped \(\rho (z)\) that represents a sea-level-density atmosphere for z < H and zero density for z ≥ H. Ensure that your lumping rectangle has the same area as the exponentially decaying \(\rho (z)\) curve.

b. Use your lumping rectangle and the sea-level pressure p₀ to estimate H. Then estimate the relative density at the top of Mount Everest (roughly 9 kilometers). Check your estimate by looking up the actual air density on Mount Everest.