12.3: MIMO using Model Predictive Control
- Page ID
- 22518
Introduction
This section describes how to control a system with multiple inputs and outputs using Model Predictive Control (MPC). MPC is a linear algebra method for predicting the result of a sequence of control variable manipulations. Once the results of specific manipulations are predicted, the controller can then proceed with the sequence that produces the desired result. One can compare this controller method to "look ahead" in chess or other board games. In look ahead, you foresee what an action might yield some time in the future using specific knowledge of the process (or game in the case of chess), and are thereby able to optimize your actions to select for the best long term outcome. MPC methods can prevent an occurrence with conventional PID controllers in which actions taken achieve short term goals, but end up very costly in the end. This phenomenon can be described as "winning the battle but losing the war."
The open ended nature of MPC allows the process control engineer use MPC to control any system for which models can be generated.
Model Predictive Control
MPC is a widely used means to deal with large multivariable constrained control issues in industry. The main aim of MPC is to minimize a performance criterion in the future that would possibly be subject to constraints on the manipulated inputs and outputs, where the future behavior is computed according to a model of the plant. The model predictive controller uses the models and current plant measurements to calculate future moves in the independent variables that will result in operation that honors all independent and dependent variable constraints. The MPC then sends this set of independent variable moves to the corresponding regulatory controller set-points to be implemented in the process.
MPC uses the mathematical expressions of a process model to predict system behavior. These predictions are used to optimize the process over a defined time period. An MPC controller can operate according to the following algorithm.
- Development of a process model by the control engineers.
- At time t, previous process inputs and outputs are used, along with the process model, to predict future process outputs \(u(f)\) over a "prediction horizon."
- The control signals that produce the most desired behavior are selected.
- The control signal is implemented over a pre-defined time interval.
- Time advances to the next interval, and the procedure is repeated from step 2.
This is one of the many algorithm possibilities, which can be applied to systems with any number of inputs or outputs. The process model can be variable as well. Examples include physical models, input-output models, and state models which are all derived from the specific system being controlled.
When comparing predicted behavior to desired behavior, there are multiple techniques. A common procedure is to generate a second mathematical model that describes your desired behavior. When process behavior is predicted in step 2 of the MPC algorithm, the control signals which produce the predicted behavior that minimize deviations from your desired behavior over the \([t,t+h]\) interval, are selected. The generation of models and optimization process is repeated continuously as the algorithm is repeated.
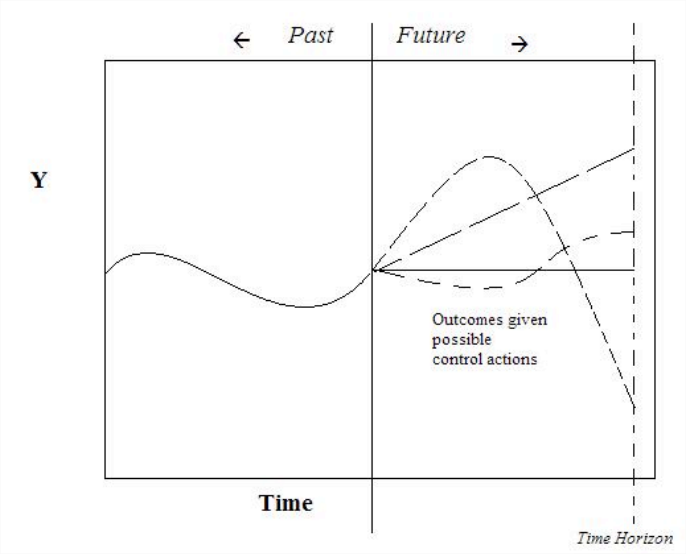
As seen in the figure above, depending on the algorithm, MPC may generate possible outcomes given possible controller action. These generations are either based on past process outputs, or the process model. After many possible outcomes are generated, the controller can pick one based on the optimization goals. This generation and optimization process is repeated at every time step.
The flow diagram below depicts the flow of information used by the controller.
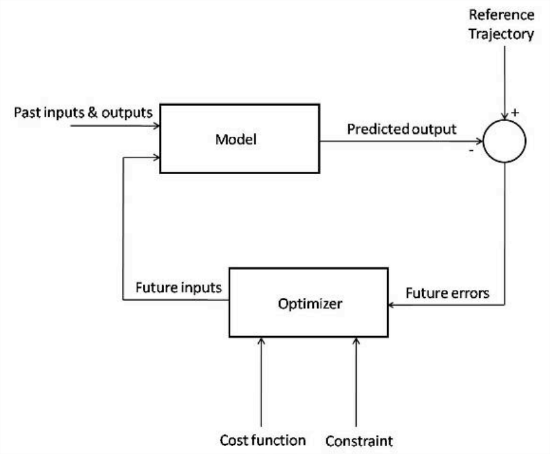
The figure above shows the basic structure of a Model Predictive Controller. The model takes data from past inputs and outputs, and combines it with the predicted future inputs, and gives a predicted output for the time step. This predicted output is combined with the reference trajectory, giving the predicted future errors of the system. These errors are fed into an optimizer, which enforces the constraints of the system (for instance, ensuring that a flow rate calculation for the model is not greater than the maximum flow) on the predicted outputs and minimizes the operating cost function. This gives the predicted future inputs, which are fed back into the main model, restarting the cycle.
Motivation
The motivation for the development and implementation of MPC controllers is compelling. MPC is very simple for sampled systems in which the control signal is constant over the interval [t,t+h]. The value of h can then be taken as the sampling interval, and the prediction horizon can become a small number of sampling intervals. This can reduce the computational power needed to implement a model predictive controller.
A highly desired feature of MPC is that constraints can be implemented in the controller. These constraints include heaters and valves that have a finite operating range, actuators with finite states (on/off or low/high), and cost or energy limits for the process. MPC can incorporate these constraints and eliminate the possibility of variables exceeding their limits. This helps the process operate efficiently, prevents damage to equipment, and prevents the system from running away by continuously increasing a variable's setting when the limit for the equipment has already been reached. Another benefit of MPC controllers incorporating system constraints is the ability of the model to dynamically react to system changes. For example, if a valve is stuck open, it can be added as a constraint, and the model will compensate accordingly. This allows the controller to continue effectively controlling the system after an equipment malfunction. In a simpler control, such as PID control, this would not be possible.
MPC is a highly specific method for controlling a process. Each controller is specific to the system it was designed for and the model equations, constraints, and set points will change for different systems. This means that a controller developed for a tank reactor will not be able to control an evaporation unit as the process model will be very different. This weakness in MPC brings out its biggest strength. The specificity and customizable nature of the controller will empower you with the freedom to design for exactly what is desired.
MPC is a flexible control technique that uses discrete time segments and is the most commonly applied advanced control technique in the chemical process industry. MPC helps to simplify or completely eliminate controller design and instead works as a system modeling controller. With MPC the designer does not have to worry about optimizing control parameters such as with PID control. The ability of MPC controllers to handle constraints in an optimal fashion is also a contributor to its success.
Model Predictive Control Example
To demonstrate the concepts of MPC, a general example for the development of a sampled process and a first-order system will be shown.
General Model
Take Equation \ref{1} as our process model:
\[y(t)+a_{1} y(t-h)+\ldots+a_{n} y(t-n h)=b_{1} u(t-h)+b_{2} u(t-2 h)+\ldots+b_{n}(t-n h) \label{1}\]
where \(u\) is controller input, \(y\) is process output, and \(h\) is the time interval. This is a general equation that relates previous process output \(y(t − h)\) and previous controller input \(u(t − h)\). In some situations this equation may be created using fitted experimental data, but is most often a derivation using knowledge of your specific system and fundamentals of chemical engineering. At time t, total previous behavior yp is shown as Equation \ref{2}.
\[y_{p}=f(y(t), y(t-h), \ldots, u(t-h), u(t-2 h), \ldots) \label{2}\]
Future process output \(y_f\) can be predicted using current and future control signals, \(u(t)\) and \(u(t + h)\) respectively:
\[y_{f}=f(u(t), u(t-h), \ldots, u(t+N h)) \label{3}\]
Both \(y_p\) and \(y_f\) could possibly be created by fits of experimental data, but are more likely to be derived from specific equations related to your system. Deviations from the desired behavior \(y_d\), either specified by another mathematical model or reference trajectory, produce an error function \(e(t) = y(t) − y_d(t)\) for increments of control actions \(Δu(t) = u(t) − u(t − h)\). The loss function \(J\) to be minimized is shown as Equation \ref{4}.
\[J(u(t), u(t-h), \ldots, u(t+N h))=\sum_{l=1}^{t \mid N} e(t+k h)^{2}+\rho(\Delta u(t+(k-1) h))^{2} \label{4}\]
The control inputs that minimize Equation \ref{4} are then applied to the system by the controller over the time interval, and the process is repeated. The control input function \(F\) in Equation \ref{5} is determined implicitly by the optimization.
\[u(t)=F(y(t), y(t-h), \ldots y(t-n h), u(t-h), y(t-2 h), \ldots, u(t-n h)) \label{5}\]
This general model is meant to be a guideline, and the equations listed representative, for the thought process required to create a model predictive controller.
First-Order System Example
Take the process model to be Equation \ref{6}:
\[\Delta y(t+h)=-a \Delta y(t)+b \Delta u(t) \label{6}\]
Let us define \(Δy(t) = y(t) − y(t − h)\) and \(Δu(t) = u(t) − u(t − h)\). Let us also define our desired system behavior \(y_d\) as a function which starts at \(y(t)\) and exponentially approaches a set point \(y_{sp}\) with time constant \(T\). Our desired behavior \(y_d\) then becomes Equation \ref{7}:
\[y_{d}(t+h)=y(t)+\left(1-e^{\frac{-h}{T}}\right)\left(y_{s p}-y(t)\right) \label{7}\]
Assuming that our controller can take as much action as needed to produce the desired behavior, the desired behavior can be realized in the next sampling period. This is done by setting \(y(t + h)\) equal to \(y_d(t + h)\), and can be seen in Equation \ref{8}:
\[y(t+h)=y(t)+\Delta y(t+h)=y(t)-\alpha \Delta y(t)+b \Delta u(t)=y(t)+\left(1-e^{\frac{-h}{T}}\right)\left(y_{s p}-y(t)\right) \label{8}\]
Solving Equation \ref{8} for \(u(t)\) gives Equation \ref{9}:
\[\Delta u(t)=\frac{a}{b} \Delta y(t)+\frac{1-e^{\frac{-h}{T}}}{b}\left(y_{s p}-y(t)\right) \label{9}\]
Upon examination of this result, you can see that we have produced a PI controller with gains \(k=\frac{a}{b}\) and \(k_{i}=\frac{1-e^{\frac{-h}{T}}}{b}\). It should be noted that the proportional gain k will only depend upon the developed process model, and the integral gain ki depends on both the process model and the desired response rate T.
This process can be modified to include multiple inputs and outputs via the process model and desired behavior. We may also add system constraints to our MPC example by adding conditional statements limiting the maximum controller output discussed in the logical programs wiki. As discussed before, there are as many variations on the MPC process as you can think of. See the worked examples 1 and 2 for more MPC instances.
Is the above expression a PI control system or more of a PD control system? The first term is k*(y(present0)-y(past)) which seems more like a derivative term. The second term is more like k*(y(set)-y(present)) which seems more like a P term.
Differences from Other Controllers Types
Model predictive control uses a mathematical model to simulate a process. This model then fits the inputs to predict the system behavior. In this way, MPC is a type of feed forward control. It uses system inputs as a basis of control. MPC is more complex than most other feed forward control types because of the way these predictions are used to optimize a process over a defined amount of time. Most feed forward control types do not take into account the process outputs much past a residence time. The MPC algorithm will compare predicted outputs to desired outputs and select signals that will minimize this difference over the time selected. This control type can see ahead into multiple time steps in the future in order to optimize the process. Normal PID type controllers use mathematical expressions based on error from a set point. The governing equation for MPC controllers are based on set points, system properties, and desired outcomes and optimization.
MPC is very specific to the process it is modeling. Unlike ratio or cascade control set ups, where it is simple to implement and change set points in various situations, MPC will model one specific process and optimize it. As previously mentioned this can either be an advantage or disadvantage. MPC is great for selecting one type of operation on one system and perfecting it to the desired conditions. This also has a downside in that the model equation will work for one and only one situation.
Limitations of MPC
Advantages of MPC
- MPC can be used to handle multivariable control programs.
- MPC can consider actuator limitations.
- MPC can increase profits by allowing for operation close to the system constraints.
- MPC can perform online computations quickly.
- MPC can be used for non-minimal phase and unstable processes.
- MPC is easy to tune.
- MPC is able to handle structural changes.
Disadvantages of MPC
- Several MPC models are limited to only stable, open-loop processes.
- MPC often requires a large number of model coefficients to describe a response.
- Some MPC models are formulated for output disturbances, and they may not handle input disturbances well.
- Some forms of MPC use a constant output disturbance assumption. This corrects for the fact that the output predicted by the model is not exactly equal to the actual measured output. This method assumes the correction term is constant in the future, which may not yield a good performance if there is a real disturbance at the plant input.
- If the prediction horizon is not formulated correctly, control performance will be poor even if the model is correct.
- Some systems have a wide range of operating conditions that change frequently. Some examples of this include exothermic reactors, batch processes, and any systems where different consumers have different product specifications. An MPC linear model will not be able to handle the dynamic behavior of these processes. A nonlinear model must be used for better control performance.
Industrial MPC Applications
There are many industrial applications that incorporate model predictive control in order to effectively control a multivariable system. In order to effectively do this, one needs to set up a working model by testing many different parameters in a plant. This is usually done by starting up a plant, varying many different parameters, and having the MPC program analyze the data.
In order to test the plant, one may vary parameters such as:
- feed flow rate/composition
- steam pressure
- heat duty
- recycle ratio
- reactor temperatures
This is only a small sample of parameters that can be changed. Once these parameters have been changed, the data is analyzed, and downstream effects of these parameters are characterized as a function of these variables. This relationship can be a combination of many different relationships (linear, nonlinear, logarithmic, exponential, power, etc.).
By testing the plant thoroughly and coming up with a robust model, the engineers ensure that an MPC controller will be able to much more effectively run the plant. Barring any major process changes, this model should be accurate for normal use.
Some industrial MPC applications are:
- Model Predictive Heuristic Control by Richard et al. 1976 (Adersa)
- Dynamic Matrix Control (DMC) by Cutler and Ramaker 1979 (Shell Oil)
- Quadratic-Program Dynamic Matrix (QDMC) Control by Cutler et al. 1983 (Shell Oil)
- IDCOM-M by Setpoint, Inc (part of ASPEN Technology)
- Generalized Predictive Control (GPC)
Implementing MPC using Excel
In MPC, values of the control variables will be optimized for a given time interval in order to best tell the system how it should act. The control variables will be optimized by optimizing some characteristic. Usually, this characteristic is simply the least squared error between an actual state and a "set" or desired state. This can easily be done using the Solver tool in Excel. See MPC_in_Excel for an example of implementing MPC to control the valve, v1, in the following system (keep reading to learn about everything in the Excel file).

To describe this system in words, there is a variable feed, Fin, with time that pours into a storage tank. The flow out of the tank, Fout, is controlled by the valve, v1, multiplied by a constant of proportionality, k1 = 50. The tank volume is to be maintained at 150.
There are three scenarios contained in the example Excel file. In the first scenario, the valve is continuous and in the second, it is binary (can be open or closed only). In the third scenario, the valve is still binary; however, Solver cannot recognize this setup even though this setup may seem intuitive (this is discussed further below). As it turns out, it doesn't really matter if a binary or continuous valve is used. Both types of valves yield very similar results; however, the continuous valve yields slightly tighter control over the tank volume (see screenshot below).
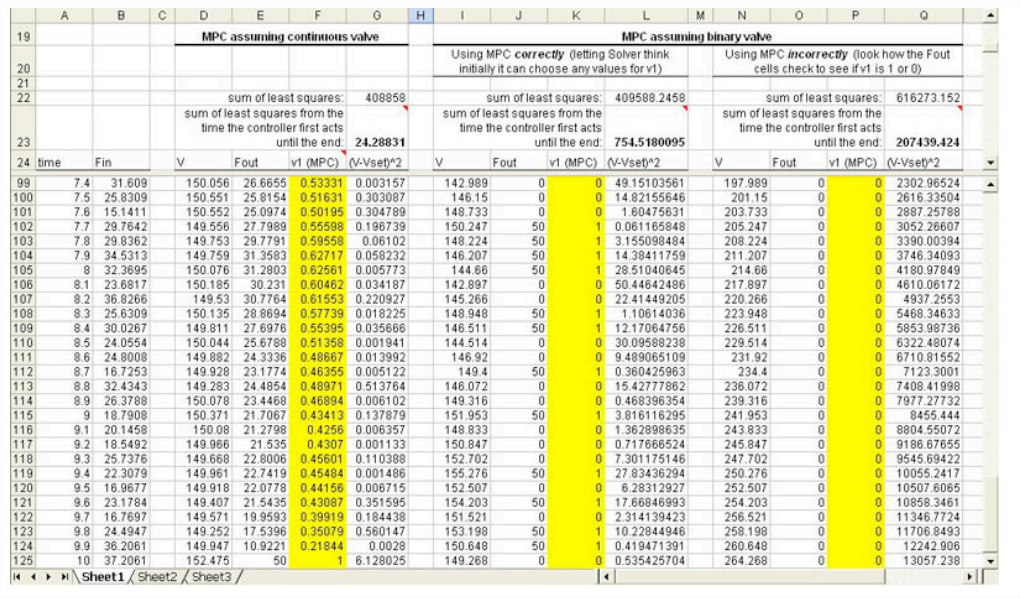
As you can see from this screen shot, the sum of the least squares between the actual volume and the set volume (Row 22) is lowest for the 1st scenario, when the valve is continuous. This measure of deviation from the set value is only slightly lower than in the 2nd scenario, when the valve is binary. In the 3rd scenario, Solver didn't work properly, resulting in all of the v1 variables (Column P) to be set to 0.
At the start of the simulation, the volume of the tank is 0, so v1 stays closed until time = 5.4 when the volume is very close to the set volume. If the deviations that occurred during the time v1 was closed (which is the same time length for all 3 scenarios) is removed from the sum of the least squares (Row 23) the 1st scenario suddenly looks much better at controlling the volume than the 2nd scenario.
There are a couple things to note while using Solver in Excel to perform MPC:
1) This note only applies if your system has a binary control variable. If you intend to use a conditional statement (such as an IF() function) that depends on the optimization of the control variable, you must leave open the possibility that this control variable can be any real number, whether it's binary or not. This may seem unnecessary because Solver will output only optimized discreet numbers. To put this in the context of the example Excel file, you might think you could have simply done the following to control Fout:
- = IF(v1 = 1, k1*1, 0)
(The variables "v1" and "k1" are not recognized by Excel. Instead of typing the variables into Excel, cells containing the variable values must be referenced.)
This statement says that if the valve is open, allow a flow of k1 (or 50), otherwise, the flow is 0. This would not allow Solver to work properly. If Solver chose a value of v1 = 0.1, measured the target cell, and then it chose v1 = 0.2, it wouldn't see any difference because in both cases the flow would be 0. Solver needs to be able to see a change in the system, whether it's practical or not, to determine the actual gradient of your system. This gradient cannot be determined if an IF() statement turns the continuous output to discreet output.
The proper way to handle this is to program a constraint into solver that allows only binary outputs of v1 values (select bin from the pull down menu when adding the constraint). \(F_{out}\) can then be programmed as:
- = v1 * k1
Using this method, Solver can calculate the gradient of the system to define how it would react if v1 changed to a non-binary value. By using this method, Solver will output only binary values for the valve state as is desired.
2) Solver can only handle manipulating 200 variables at a time, so if your model requires looking at more than 200 time steps, you will have to optimize your system in sections.
You have a tank outside your home used to supply water for various household functions (i.e. flushing the toilet). The optimal water pressure from the tank is achieved when the height of water in the tank is at 15, and the tank can hold water up to a height of 30, because when it rains, it pours. When it does rain, the level of water in this tank exceeds 15 and a model predictive controller and valve is in place to release water so the height will drop back down to this value (don't worry, this water is not wasted, but used as drinking water on your llama farm). At time t=25, there is a downpour that increases the flow into the tank by 150 and lasts for 100 time steps. Will this tank overflow, and how long will it take for the tank to return to the desired set point? Your controller output is 25 maximum.
Other key pieces of info:
- H(0)= 15
- A= 100
- B= 1
- T= 15
- Hset= 15
- h= 1
Solution
To obtain the required information, we will produce a model predictive controller for the water tank system, and simulate how the system will behave during the downpour. The first step is to generate a mathematical model that describes the relevant parameters. Equation \ref{10} below relates the fluid height in the tank \(H\) to the flow in, and controller signal \(u\).
\[A \frac{d H}{d t}=F_{i n}-B u \sqrt{H(t)} \label{10}\]
where \(A\) and \(B\) are physical constants of the system. Next we will define the way we wish the height of fluid in the tank to act in Equation \ref{11}.
\[H(t+h)=H(t)+\left(1-e^{-h / T}\right)\left(H_{s e t}-H(t)\right) \label{11}\]
Where h is the time interval, T is an exponential time constant, and Hset is the desired liquid set point of 15. It can be seen by examining equation 11 that as time proceeds, the exponential term will reduce to zero, resulting in H(t + h) = Hset. The next step is to figure out how to produce a controller input that will give the desired behavior. This may be done by calculating the error between process model and desired behavior, and optimizing for u. Fortunately for us, this is a relatively simple set of equations that can be solved for u explicitly. By expanding Equation \ref{10} using the fundamental theorem of calculus to produce Equation \ref{12}, and plugging Equation \ref{11} in for H(t + h), equation 13 results solved for u.
\[A \frac{H(t+h)-H(t)}{h}=F_{i n}-B u \sqrt{H(t)} \label{12}\]
\[u=\frac{\left(-A H_{s e t}+A H(t)+A e^{\frac{-h}{T}} * H_{s e t}-A e^{\frac{-h}{T}} H(t)+F_{\text {in }} h\right)}{\left(B \sqrt{H_{s e t}} h\right)} \label{13}\]
These equations can be implemented in a spreadsheet to model the behavior of the height of liquid in the tank, as well as the actions taken by the controller to restore the set point. Keep in mind the 0 to 25 output restriction on your controller.
This spreadsheet has been made with the relevant equations and can be used to solve this problem and model tank behavior. This spreadsheet can be found here:MPC example 1
So yes, the tank will overflow, and will return to its set point after 200 time points.
What happens if the actuator on the valve breaks and must be replaced with an older one you happened to have in your basement? This new (although old) actuator cannot operate the valve fast enough, and B is decreased from 1 to 0.8. How does the graph from example 1 change? What does this tell you about the physical meaning of parameter B?
Solution
This B can easily be changed in the spreadsheet used in example 1. With this different actuator, and hence different B, we can see that the tank acquires more volume, and it takes longer for the tank to return to its optimal height of 15. This is because the valve on the tank cannot be opened as fast. Parameter B represents the physical properties/limitations of the valve, and pipe properties.
Sage's Corner
- www.youtube.com/v/XNccO4neVfc
- www.youtube.com/v/2HkpKgXlyfE
Which of the following is a highly desired feature for model predictive control?
- It is ideal in determining short-term behavior.
- It is the simplest of all feed forward controller types.
- It accounts for system constraints.
- Controllers of this type are universal and can be used without modification for any process.
- Answer
-
C
Will a model predictive controller developed for a tank reactor be able to control an evaporation unit?
- Yes, as they are both standard pieces of chemical engineering equipment.
- Maybe, it depends if the reaction taking place in the reactor is exothermic or endothermic.
- No, the governing equations will be very different.
- Yes, because evaporation units and tank reactors can both use steam to supply heat.
- Answer
-
C
Which of the following statements about MPC is false?
- MPC uses a defined time interval.
- MPC utilizes feed forward control.
- MPC requires a certain number of inputs and outputs.
- MPC can generate more than one possible outcome.
- Answer
-
C
References
- Astrom, Karl J. and Hagglund, Tore. Advanced PID Control, Department of Automatic Control, Lund Institute of Technology, Lund University.
- Bequette, B. Wayne. Process Control: Modeling, Design and Simulation. Prentice Hall PTR. pp. 487-511, December 26, 2002.
- Garcia C.E, Prett D.M. and Morari M. Model Predictive Control: Theory and Practice - a Survey. Automatica, Vol.25, No.3, pp. 335-348, 1989.
- Orukpe, P.E. Basics of Model Predictive Control. Imperial College, London. April 14, 2005.


