5.6: Problems

Problem \(5.1\)

The motion of a particle is described by the relation \[x = \left( 3.0 \ \frac{\mathrm{m}}{\mathrm{s}^{3}} \right) t^{3} - \left(6.0 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right) t^{2} - \left(12.0 \ \mathrm{ft} \frac{\mathrm{m}}{\mathrm{s}}\right) t + (5.0 \ \mathrm{ft}) \nonumber \] The particle has a mass of 5 kilograms and all motion is in a horizontal plane, i.e. gravity has no effect. Answer the following questions:

(a) Determine when the velocity is zero.

(b) Determine the position and the total distance traveled when the acceleration is zero.

(c) Determine the linear momentum and the rate of change of the linear momentum of the particle for \(t=0,1,2,3,\) and \(4\) seconds.

(d) Graph the linear momentum and the rate of change of the linear momentum of the particle as a function of time for \(0 \leq t \leq 4\) seconds. [Note: you may need more than 5 points to accurately plot this function.]

• What is the maximum value of the linear momentum of the particle during this time interval and when does it occur?
• What is the maximum value of the rate of change of the linear momentum of the particle and when does it occur?

(e) Using conservation of linear momentum for this particle, determine the net external force acting on the particle for \(t=0,1,2,3,\) and \(4\) seconds.

(f) Graph the net external force acting on the particle as a function of time for 0 \(\leq t \leq 4\) seconds. [Note: you may need more than 5 points to accurately plot this function.]

• What is the maximum value of the net external force acting on the particle during this time interval and when does it occur?
• Does the direction of the net external force change during this time interval? If so, when does it occur?

(g) Compare your results for (c), (d), (e), and (f). Comment on similarities and differences.

Problem \(5.2\)

A rocket sled weighing \(3,220 \ \text{lbf}\) reaches a constant speed of \(700 \ \mathrm{ft} / \mathrm{s}\) under a thrust force of \(8,000 \ \mathrm{lbf}\). The primary resistance to motion is a fluid drag force with a magnitude of \(F_{\text {drag}}=k V^{2}\) and a direction that opposes the motion.

(a) Determine the value of the constant \(k\) in the drag force model.

(b) If the engine is shut off, determine how long it takes and how far the sled travels as it slows down to \(70 \ \mathrm{ft} / \mathrm{s}\).

Problem \(5.3\)

Two cables are tied together at \(C\) and are loaded as shown. The entire system is stationary. You must sketch a complete linear momentum interaction diagram (also called a free-body diagram) for each problem clearly showing the important transports of linear momentum.

Figure \(\PageIndex{1}\): A loaded cable system.

(a) Starting with the rate-form of the conservation of linear momentum, use the closed system shown by the dashed line to solve for the tension in the cables \(A C\) and \(B C\).

(b) How would your analysis change if you used a closed system that only included the joint at \(C\)? How would you handle the force applied by the hanging object?

(c) What would the tension be in both cables if the angle for both \(A C\) and \(B C\) was \(5^{\circ}\) ? What is the ratio of the tension in each cable to the weight of the mass? This ratio is sometimes referred to as the mechanical advantage you learned about when you studied levers. Does this give you any ideas about what would be the best way to rig up a cable to pull a car up an embankment? Any problems with your idea?

Problem \(5.4\)

A tractor-trailer is traveling at \(60 \ \mathrm{mi} / \mathrm{h}\) when the driver applies her brakes. The tractor has a mass of \(15,000 \ \mathrm{lbm}\), and the trailer has a mass of \(17,400 \ \mathrm{lbm}\). Knowing that the braking forces of the tractor and the trailer are \(3600 \ \mathrm{lbf}\) and \(13,700 \ \mathrm{lbf}\), respectively, determine (a) the distance traveled by the tractor trailer before it comes to a stop, and (b) the horizontal component of the force in the hitch between the tractor and the trailer while they are slowing down.

Remember to start with the appropriate conservation equations and carefully select your system and identify the important interactions between the system and the surroundings. Also, remember to draw a free body diagram (linear momentum interaction diagram). [Hint: Use two different systems to answer the questions. For part (a) take the entire truck and trailer as the system. For part (b) use either the truck or the trailer for your analysis. Note that since the truck and trailer are hooked together, information like acceleration and velocity you calculate in part (a) can be used directly in part (b) without redeveloping the information. Why do you need to use this system for part (b)?]

Why does atmospheric pressure cancel out in this problem — or does it?

Problem \(5.5\)

(Adapted from Dynamics by Beer & Johnson, 6th edition)

A man hosing down his driveway hits the back of his mailbox by mistake. The velocity and cross-sectional area of the water stream as it hits the back of the mailbox are \(25 \mathrm{~m} / \mathrm{s}\) and \(300 \mathrm{~mm}^{2}\), respectively. The water stream is horizontal as it hits the vertical surface of the mailbox. Assume all systems are steady-state and answer the following questions. Carefully show all of your work, especially how you create an appropriate model for this system starting with the rate form of the linear momentum equation. If needed, assume atmospheric pressure to be \(100 \ \mathrm{kPa}\).

Figure \(\PageIndex{2}\): Behavior of a water stream as it hits a vertical side of a mailbox.

(a) Determine the direction and magnitude, in Newtons, of the horizontal shear force that is applied by the post to the mailbox. [Hint: Pick an open system that cuts the wooden post and the water stream. For this system, there is only one contact force with a horizontal component. Assume all water enters the system with a horizontal velocity of \(25 \mathrm{~m} / \mathrm{s}\) and that it leaves the system with no horizontal component of velocity.]

(b) Now determine the direction and magnitude, in Newtons, of the force of the water acting on the mailbox. Is this answer different than your answer above? [Hint: This time pick a closed system, the mailbox. For this system, the water force appears as a contact (or surface) force acting on the boundary of the system. Be careful to consider the pressure forces acting on the system.]

Answer

a) \(187.5 \mathrm{~N}\) acting to the left.

b) Yes, it is greater than the answer in part (a).

Problem \(5.6\)

Water flows steadily through a \(180^{\circ}\) reducing pipe bend as shown in the figure. The atmospheric pressure outside the piping system is \(P_{\mathrm{atm}}=100 \ \mathrm{kPa}\). The pipe bend is connected to the two pipes by flanges. The flanges are held together by flange bolts. Assume the density of water is \(1000 \mathrm{~kg} / \mathrm{m}^{3}\).

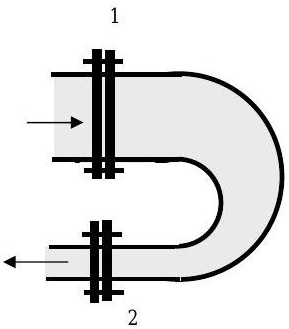
Figure \(\PageIndex{3}\): Water moves through a reducing pipe bend shaped in a semicircle.

At the inlet to the bend, the pressure is \(P_{1}=350 \ \mathrm{kPa}\), the pipe diameter is \(D_{1}= 25 \mathrm{~cm}\), and the water velocity is \(V_{1}=2.2 \mathrm{~m} / \mathrm{s}\). At the outlet of the bend, the pressure is \(P_{2}=120 \ \mathrm{kPa}\) and the pipe diameter is \(D_{2}=8 \mathrm{~cm}\).

Neglecting the weight of the pipe bend and the water in the bend, determine the magnitude and direction of the total force (not force in the \(x\)-direction) of the flange bolts on the pipe bend. Would it have been "OK" to neglect the pressure effects?

Problem \(5.7\)

(Adapted from Dynamics by Beer & Johnson, 6th edition)

A light train made of two cars travels at \(45 \ \mathrm{mi} / \mathrm{h}\). Car \(A\), which is in the front of the train, weighs 18 tons and car \(B\) weighs 13 tons. A constant breaking force of \(4300 \ \mathrm{lbf}\) is applied to car \(B\) but the brakes on car \(A\) are not applied. Determine (a) the time required for the train to stop after the brakes are applied, and (b) the force in the coupling between the cars which the train is slowing down.

Answer

(a) \(29.6 \mathrm{~s}\) and (b) \(2500 \ \text{lbf}\) in tension

Problem \(5.8\)

A block of mass \(m_{2}\) is placed on a wedge-shaped block of mass \(m_{1}\). The angle of the wedge is \(\theta\). The inclined surface is frictionless and the small block slides freely on the incline. In addition, the small casters under the wedge are also frictionless, so the wedge glides freely on the horizontal surface.

Figure \(\PageIndex{4}\): A system where a force is exerted on a wedge on which a block rests.

(a) Determine the value of applied force \(P\), in Newtons, that must be applied so that the smaller block will not slip on the wedge-shaped block, i.e. is no relative motion between the two blocks.

(b) How fast will the blocks be accelerating, in \(\mathrm{m} / \mathrm{s}^{2}\) ?

Note: It may not be possible to solve this problem using only one system

Problem \(5.9\)

A \(20 \text{-kg}\) package is at rest on an incline when a force \(\mathbf{P}\) is applied to it. The coefficients of static and kinetic friction between the package and the incline are \(0.4\) and \(0.3\), respectively.

Figure \(\PageIndex{5}\): A system where a force is exerted on a package on an incline.

(a) Determine the minimum force \(\mathbf{P}\) required to move the package.

(b) Determine the magnitude of \(\mathbf{P}\) if \(10 \mathrm{~s}\) is required for the package to travel \(5 \ \mathrm{m}\) up the incline.

Problem \(5.10\)

(Adapted from Dynamics by Beer & Johnson, 6th edition)

The triple jump is a track-and-field event in which an athlete gets a running start and tries to leap as far as he can with a hop, step, and jump. The runner approaches the takeoff line from the left with a horizontal velocity of \(10 \mathrm{~m} / \mathrm{s}\), remains in contact with the ground for \(0.18 \mathrm{~s}\), and takes off with a velocity of \( 12 \mathrm{m} / \mathrm{s}\) at an angle of \(50^{\circ}\) from the horizontal.

Determine the vertical component of the average impulsive force exerted by the ground on his foot. Carefully identify your system and the associated transfers of linear momentum. Give your answer in terms of the weight \(W\) of the athlete.

Problem \(5.11\)

(Adapted from Dynamics by Beer & Johnson, 6th edition)

Two swimmers \(A\) and \(B\) of weight \(190 \ \mathrm{lbf}\) and \(125 \ \mathrm{lbf}\), respectivey, are at diagonally opposite corners of a floating raft that is \(20 \ \mathrm{ft}\) wide and \(10 \ \mathrm{ft}\) long. Suddenly they realize that the raft has broken away from its moorings and is floating free. Swimmer \(A\) immediately starts walking toward \(B\) at a speed of \(2 \ \mathrm{ft} / \mathrm{s}\) relative to the raft. Knowing that the raft weighs \(300 \ \mathrm{lbf}\), determine (a) the speed of the raft if \(B\) does not move, and (b) the speed with which \(B\) must walk toward \(A\) if the raft is not to move.

Problem \(5.12\)

(Adapted from Dynamics by Beer & Johnson, 6th edition)

A block slides up an inclined plane from point \(A\) where its velocity is \(30 \ \mathrm{ft} / \mathrm{s}\) to a point where its velocity is zero. The plane makes an angle of \(20^{\circ}\) with the horizontal. The coefficient of kinetic friction between the block and the plane is \(0.30\).

(a) Determine the time it takes for the block to travel from \(A\) to \(B\).

(b) Determine the minimum value of the static-friction coefficient that is required to keep the block from sliding back down the slope after it reaches point \(B\).

Problem \(5.13\)

(taken from Fundamentals of Fluid Mechanics by Munson, Young and Okiishi)

A vertical, circular cross-sectional jet of air strikes a conical deflector as indicated in the figure. A vertical anchoring force of \(0.1 \mathrm{~N}\) is required to hold the deflector in place. Determine the mass, in \(\mathrm{kg}\), of the deflector. The magnitude of the air velocity remains constant and the density of air is \(1.23 \mathrm{~kg} / \mathrm{m}^{3}\).

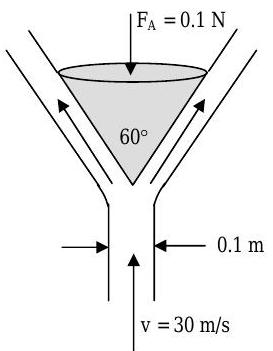
Figure \(\PageIndex{6}\): Vertical air stream splits around a tip-down conical deflector.

Problem \(5.14\)

The conveyor belt shown below moves a constant speed of \(v_{\mathrm{o}} = 24 \ \mathrm{ft} / \mathrm{s}\). The length of the belt is \(L=20 \ \mathrm{ft}\).

(a) Determine the angle \(\alpha\) for which the sand is deposited on the stockpile at B.

(b) If the sand falls with practically zero velocity onto the conveyor at a constant rate \(\dot{\mathrm{m}}=100 \ \mathrm{lbm} / \mathrm{s}\) as shown below, determine the magnitude of the net force \(\mathrm{P}\) required to maintain a constant belt speed \(v\) (use the smaller of the two angles from part a). Note: \(\mathrm{P}\) would not act at the location shown below - it is placed there for convenience only. Assume you can neglect the mass of the belt, but not the mass of the sand on the belt.

Figure \(\PageIndex{7}\): Sand falls onto an inclined conveyor belt and arcs off the end of the belt.

Problem \(5.15\)

The resistance \(R\) to penetration of a \(0.25 \mathrm{~kg}\) projectile fired with a velocity of \(600 \ \mathrm{m} / \mathrm{s}\) into a certain block of fibrous material is shown in the graph below. Represent this resistance by the dashed line and compute the velocity of the projectile for the instant when \(x=25 \mathrm{~mm}\) if the projectile is brought to rest after a total penetration of \(75 \mathrm{~mm}\).

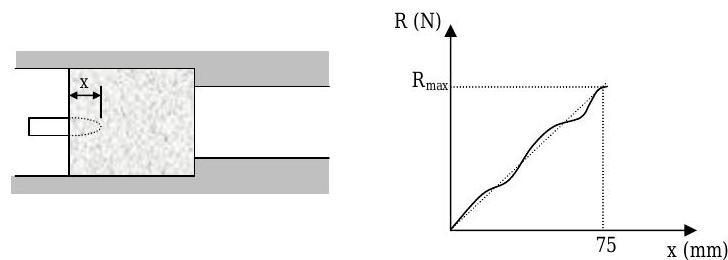
Figure \(\PageIndex{8}\): Graph of a block's penetration resistance vs distance penetrated into block by a projectile.

Problem \(5.16}\)

A \(125 \ \mathrm{lb}\) block initially at rest is acted upon by a force \(\mathbf{P}\) which varies as shown. Knowing that the coefficients of friction between the block and the horizontal surface are \(\mu_{\mathrm{s}}=0.50\) and \(\mu_{\mathrm{k}}=0.40\), determine

(a) the time at which the block will start moving

(b) the maximum velocity reached by the block

(c) the time at which the block will stop moving.

Figure \(\PageIndex{9}\): Graph showing time variation of a force exerted on a block.

Problem \(5.17\)

Boxes \(\mathrm{A}\) and \(\mathrm{B}\) are at rest on a conveyor belt that is initially at rest. The belt suddenly started in an upward direction so that slipping occurs between the belt and the boxes. The coefficients of kinetic friction between the belt and the boxes are \(\left(\mu_{\mathrm{k}}\right)_{\mathrm{A}}=0.30\) and \(\left(\mu_{\mathrm{k}}\right)_{\mathrm{B}}=0.32\).

(a) Determine the initial acceleration of each box.

(b) If the two blocks remain in contact, how long will it take them to travel \(3 \ \mathrm{ft}\)? If they separate, what will the distance between the two blocks be after \(\mathrm{A}\) has traveled up the incline \(3 \ \mathrm{ft}\)?

Figure \(\PageIndex{10}\): A system where two boxes in contact rest on an inclined conveyor belt.

Problem \(5.18\)

If the coefficient of kinetic friction between the \(20 \mathrm{-kg}\) block \(\mathrm{A}\) and the \(100 \mathrm{-kg}\) cart \(\mathrm{B}\) is \(0.50\), and the coefficient of static friction is \(0.55\), determine the acceleration of each block when:

a) \(\mathrm{P}=40 \mathrm{~N}\),

b) \(\mathrm{P}=60 \mathrm{~N}\),

c) \(\mathrm{P}=100 \mathrm{~N}\).

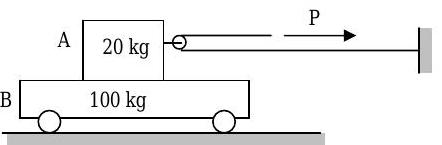
Figure \(\PageIndex{11}\): A force is applied to a box stacked on another box that can roll.

(Hint: To determine if A slides on B, assume that it doesn't and then solve for the friction force and compare to \(\mu_{s} N\) )

Problem \(5.19\)

(modified version of a problem taken from Vector Mechanics for Engineers by Beer and Johnson)

A \(10 \text{-kg}\) package drops from a chute into a \(25 \text{-kg}\) cart with a velocity of \(3 \ \mathrm{m} / \mathrm{s}\). Knowing that the cart is initially at rest and can roll freely, determine

(a) the final velocity of the cart

(b) the impulse exerted by the cart on the package.

Figure \(\PageIndex{12}\): A box falls at an angle towards a open cart.

Problem \(5.20\)

(modified version of a problem taken from Vector Mechanics for Engineers by Beer and Johnson)

At an intersection car \(\mathrm{B}\) was traveling south and car \(\mathrm{A}\) was traveling 30 degrees north of east when they slammed into each other. Upon investigation it was found that after the crash the two cars got stuck and skidded off at an angle of 10 degrees north of east. Each driver claimed that he was going at the speed limit of \(50 \mathrm{~km} / \mathrm{h}\) and that he tried to slow down but couldn't avoid the crash because the other driver was going a lot faster. Knowing the mass of the two cars \(\mathrm{A}\) and \(\mathrm{B}\) were \(1500 \ \mathrm{kg}\) and \(2000 \ \mathrm{kg}\), respectively, determine

(a) which car was going faster

(b) the speed of the faster car if the slower car was traveling at the speed limit.

Figure \(\PageIndex{13}\): Directions of travel of two cars, before and after they collide.

Problem \(5.21\)

(modified version of a problem taken from Vector Mechanics for Engineers by Beer and Johnson)

A mother and her child are skiing together, with the mother holding the end of a rope tied to the child's waist. They are moving at a speed of \(7.2 \mathrm{~km} / \mathrm{h}\) on a flat portion of the ski trail when the mother observes that they are approaching a steep descent. She decides to pull on the rope to decrease her child's speed. Knowing that this maneuver causes the child's speed to be cut in half in \(3 \mathrm{~s}\) and neglecting friction, determine

(a) the mother's speed at the end of the \(3 \text{-s}\) interval

(b) the average value of the tension in the rope during that time interval.

Figure \(\PageIndex{14}\): A mother and child skiing single file, connected by a rope

Problem \(5.22\)

(taken from Fundamentals of Fluid Mechanics by Gerhart, Gross and Hochstein)

A carbon steel, \(14 \text{-in}\) outer diameter (\(13.25 \text{-in}\) inner diameter), schedule \(30\), \(90^{\circ}\) elbow is to be butt-welded to a pipe carrying water at \(Q=4000 \ \mathrm{gal} / \mathrm{min}\).

Find the force required in the weld to support the elbow. The elbow weighs \(150 \ \mathrm{lbf}\). The density of water is \(1.94 \ \mathrm{slug} / \mathrm{ft} ^{3}\).

(Hint: The mass of water is approximately equal to \(\mathrm{m}_{\mathrm{w}} \approx \left(\pi D^{2} / 4 \right) L \rho\) where \(D\) is the inside diameter of the pipe and \(L\) is the arc length associated with \(Re\).)

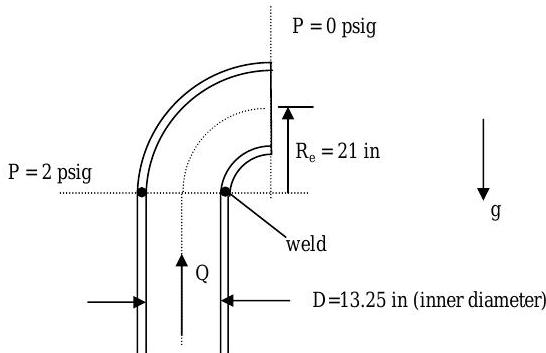
Figure \(\PageIndex{15}\): Water travels up a vertical pipe welded to a \(90^{\circ}\) elbow.

Problem \(5.23\)

A \(0.02 \mathrm{~kg}\) bullet strikes block \(\mathrm{A}\) with a velocity of \(\mathrm{v}_{0}=150 \mathrm{~m} / \mathrm{s}\) as shown below. The masses of the blocks are given in the figure. Assume the bullet becomes lodged in \(\mathrm{A}\) and the time of impact is very small.

Figure \(\PageIndex{16}\): Bullet moves towards one of two stacked blocks.

Determine:

(a) the velocity of \(\mathrm{A}\) after the impact,

(b) the acceleration of \(\mathrm{A}\) and \(\mathrm{C}\) after the impact, and

(c) the time it will take for block \(\mathrm{C}\) to stop sliding on block \(\mathrm{A}\). (Assume block \(\mathrm{A}\) is large enough so that \(\mathrm{C}\) will not fall off of it.)

Hints: The friction force between the blocks is not an impulse force. There will be sliding between the blocks.

Problem \(5.24\)

A particle is traveling in a straight line in a horizontal plane. The mass of the particle is \(0.10 \mathrm{~kg}\). The acceleration of the particle is described by the following equation: \[a =\frac{dv}{dt} = A - B t^2 \nonumber \] where \(A= \text{constant}\) and \(B=6 \mathrm{~m} / \mathrm{s}^{4}\). The following additional information is known about the motion of the particle: \[\text { At } t=0: \quad x=x_{0}=8 \mathrm{~m}, \,\, V=V_{0}=0 \quad \text { and } \quad \text { At } t=1 \text { second: } \quad V=30 \mathrm{~m} / \mathrm{s} \nonumber \]

(a) Determine the time(s) at which the velocity is zero.

(b) Determine the total distance traveled when \(\mathrm{t}=5 \ \mathrm{sec}\). (Note that the change in position \(\mathrm{x}\) is not the same as the distance traveled.)

(c) Plot the acceleration, velocity, and position of the particle for \(0 \leq \mathrm{t} \leq 5 \mathrm{~seconds}\). Determine the time(s) when the motion of the particle changes direction.

(d) For the same time interval as in Part (c), plot the linear momentum of the particle, the rate of change of linear momentum of the particle, and the net external force on the particle in the horizontal plane. Determine the time(s) when the net external force changes direction.

(e) Discuss how the time(s) you calculated in Part (c) when the particle changed its direction of motion relate to the time(s) you calculated in Part (d) when the net external force changes direction. Is there any relation?

Problem \(5.25\)

(Adapted from Engineering Mechanics: Statics by Bedford & Fowler, Addison-Wesley)

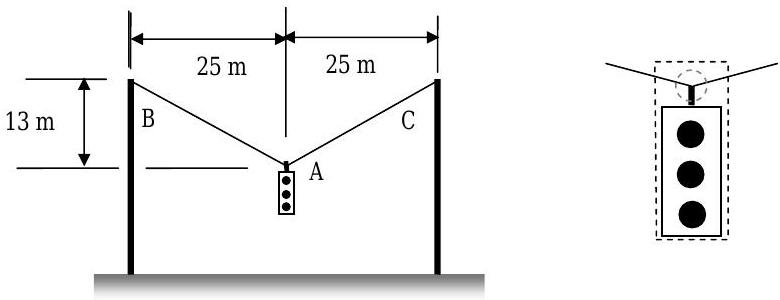
Figure \(\PageIndex{17}\): A traffic light hangs from cables connected to two posts.

A \(140 \text{-kg}\) traffic light is suspended above the street by two cables as shown in the figure above. On a windy day the wind blows from left to right on the figure and creates a horizontal force of \(200 \mathrm{~N}\) on the traffic light. Assume that the deflection of the traffic light from a vertical orientation due to the crosswind is negligible.

(a) Starting with the rate-form of the conservation of linear momentum, use the closed system shown by the dashed lines in the figure to solve for the tension in the cables \(AB\) and \(AC\) with and without the crosswind force.

(b) How would your analysis change for (a) if your system only included the intersection of the two cables and the traffic light as shown inside the light gray dashed circle? How would you handle the force applied by the hanging traffic light?

Problem \(5.26\)

A \(30 \text{-kg}\) package is placed on an incline when a force \(\mathbf{P}\) is applied to it as shown on the figure. The coefficients of static and kinetic friction between the package and the incline are \(0.2\) and \(0.1\), respectively. The motion of the package depends on the magnitude of the force \(\mathbf{P}\).

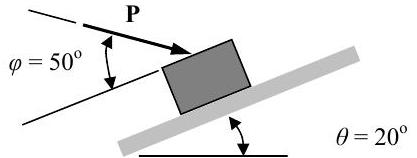
Figure \(\PageIndex{18}\): A package resting on a ramp experiences a force \(\mathbf{P}\) applied to it.

(a) Determine the range of values for \(\mathbf{P}\) for which the package will remain stationary on the inclined plane.

(b) Assuming the package is initially stationary, determine its velocity and position 10 seconds after the force \(\mathbf{P}\) is reduced to zero, i.e. \(\mathbf{P}=0\).

Problem \(5.27\)

The mass of Block \(A\) is \(30 \mathrm{~kg}\) and the mass of Sphere \(B\) is \(5 \mathrm{~kg}\). Block \(A\) slides on the surface, and as it slides Sphere \(B\) is free to move as shown in the figure. The coefficient of kinetic friction between Block \(A\) and the surface is \(0.24\). Assume that the link connecting the block and the sphere has negligible mass.

Figure \(\PageIndex{19}\): A sphere hangs from a block sliding along a surface.

(a) Determine the numerical value of the force \(F\), if the angle \(\theta=20^{\circ}\) is constant.

(b) Is the linear momentum of the block increasing, decreasing, or constant? Is the block accelerating, decelerating, or moving at constant velocity?

(c) Determine the magnitude and direction of the force of the link acting on the sphere. Is there tension or compression in the link connecting Block \(A\) and Sphere \(B\) ?

Problem \(5.28)

In a cathode-ray tube, an electron with mass \(m\) enters the gap between two charged plates at Point \(O\) with a velocity \(\mathbf{V}=V_{o} \mathbf{i}\). While it is between the charged plates, the electric field generated by the plates subjects the electron to a force \(\mathbf{F}=-e E \mathbf{j}\) where \(e\) is the charge of the electron and \(E\) is the electric field strength. The plate spacing is \(2 h\), the length of the charged plates is \(l\), and the distance to the screen is \(L\). (See figure below.) Assume that gravitational forces can be neglected and that external forces on the electron are negligible when it is not between the charge plates.

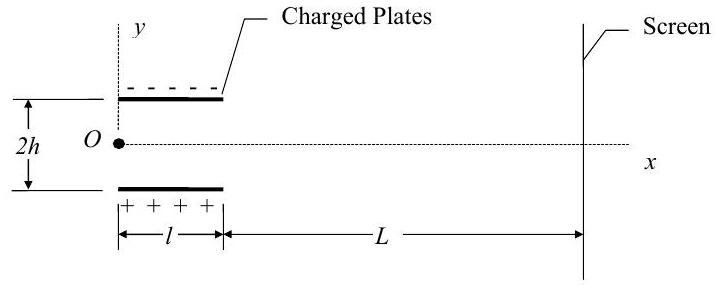
Figure \(\PageIndex{20}\): An electron passes between oppositely charged plates to impact a screen.

(a) Starting with the appropriate conservation and accounting relations, develop an expression for the location of the point of impact of the electron with the screen. Your answer should be presented in terms of the initial speed of the electron \(\left(V_{o}\right)\), the mass of the electron \((m)\), the charge of the electron \((e)\), the electric field strength \((E)\), and the dimensions \(h, \ l,\) and \(L\). Clearly identify your system and show how you use the material in the problem and any additional assumptions to develop your answer.

(b) Sketch the path of the electron on the figure.

(c) Calculate the deflection in terms of \(h\) if the following numerical values are known: \[ \begin{aligned} & V_{o}=2.2 \times 10^{7} \mathrm{~m} / \mathrm{s} ; \quad m=9.11 \times 10^{-31} \mathrm{~kg} ; \quad e=1.6 \times 10^{-19} \mathrm{C} \text { (coulombs); } \quad E=15 \ \mathrm{kN} / \mathrm{C} \\ & L=100 \mathrm{~mm} ; \quad l=30 \mathrm{~mm} \end{aligned} \nonumber \]

Problem \(5.29\)

A block with a mass \(m=200 \mathrm{~kg}\) rests on an inclined plane with an applied load \(\mathbf{P}\). Depending upon the magnitude of \(\mathbf{P}\), the block may move up the incline, down the incline, or remain stationary. Between the surfaces of contact, the coefficient of static friction is \(\mu_{\mathrm{s}}=0.25\) and the coefficient of kinetic friction is \(\mu_{\mathrm{k}}=0.20\).

Determine the range of the magnitude of the horizontal force \(\mathbf{P}\), in Newtons, that will keep the block in equilibrium, i.e. not moving.

Figure \(\PageIndex{21}\): An irregularly shaped block resting on an incline experiences a force \(\mathbf{P}\).

Problem \(5.30\)

The ducted fan unit shown in the figure has mass \(m=100 \mathrm{~kg}\) and is supported in the vertical position on its flange at \(A\). The unit draws in air with a density \(\rho=1.200 \mathrm{~kg} / \mathrm{m}^{3}\) and a velocity \(V_{1}=5 \mathrm{~m} / \mathrm{s}\) through an inlet with diameter \(D_{1}=1.00 \mathrm{~m}\). It discharges air through two outlets at the bottom of the fan. The mass flow rate through each outlet is \(1 / 2\) of the entering mass flow rate, and the velocity at each outlet is \(V_{2}=V_{3}=15 \mathrm{~m} / \mathrm{s}\). Both inlet and outlet pressures are atmospheric.

Determine the vertical force \(R\), in Newtons, applied to the flange of the fan unit by the supports.

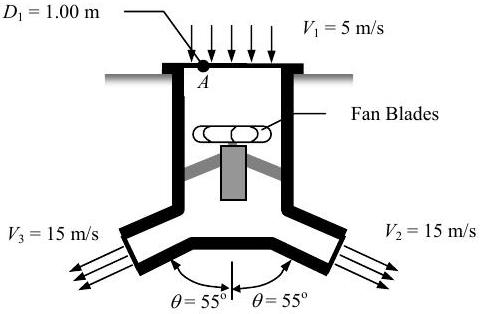
Figure \(\PageIndex{22}\): A fan unit is held in a vertical position by a flanged upper rim.

Problem \(5.31\)

A crate with mass \(m=500 \ \mathrm{lbm}\) is attached to a motorized winch and positioned on a sloping dock with inclination angle \(\theta=30^{\circ}\) as shown in the figure. The winch exerts a tensions force \(T\) on the crate through the winch cable. The friction coefficients between the crate and the dock surface are \(\mu_{\mathrm{s}}=0.30\) for static friction and \(\mu_{\mathrm{k}}=0.25\) for kinetic friction.

Initially, the crate is stationary and the winch brake is on to prevent any motion. Suddenly at \(t=0\), the brake is released and the winch exerts a constant tension force \(T=100 \ \mathrm{lbf}\) on the crate. At \(t>2\) seconds, the tension force exerted by the winch on the crate suddenly increases to a constant value \(T=400 \ \mathrm{lbf}\).

2 seconds, the winch operates with the cable tension force being 400 lbf." src="/@api/deki/files/54938/Screenshot_(79).png">

Figure \(\PageIndex{23}\): A crate is pulled up a ramp by a cable attached to a winch. Cable tension varies as a function of time.

(a) Consider the forces on the stationary crate when the winch brake is on and find the value or range of values for the tension force \(T\) under these conditions.

(b) Consider the crate's motion for \(0 \leq t \leq 2 \mathrm{~s}\) when the tension force is \(T=100 \ \mathrm{lbf}\). Find the crate's acceleration, velocity and position at \(t=2\) seconds.

(c) Consider the crate's motion for the period \(t>2 \mathrm{~s}\) when the tension force is \(T=400 \ \mathrm{lbf}\). Qualitatively describe how the crate moves during this period (Be concise; use words and not numbers!)

(d) Calculate the impulse for the tension force \(T\) over the time interval \(t=0\) to \(4 \ \mathrm{s}\). Be sure to indicate both the direction and magnitude.

Problem \(5.32\)

You have been asked to investigate the performance of a jet-propelled boat using a water channel where the water velocity \(V_{\text {water}}\) can be varied as required. The boat is placed in the channel and tethered so that it is stationary. The boat is jet-propelled by a pump that develops a constant volumetric flow rate of water, \(\dot{V\kern-0.8em\raise0.3ex-} _{\text {pump}}\). Water enters the aft (front) of the boat through an area of \(A_{1}\) and leaves at the stern (rear) through an area \(A_{2}\).

Water flowing over the hull of the boat exerts a drag force on the boat in the direction the water is flowing. This horizontal drag force which includes the net pressure forces on the hull is given by the following equation: \[F_{\text {drag}}=k V_{\text {water}}^{2} \nonumber \] where \(k\) is a constant.

Assume that the angle \(\theta\) and water density \(\rho\) are both known.

a) Find expressions for the water velocities \(V_{1}\) and \(V_{2}\) in terms of the pump flow rate, \(\dot{V\kern-0.8em\raise0.3ex-}_{\text{pump}}\).

b) Find an expression for the volumetric flow rate through the pump \(\dot{V\kern-0.8em\raise0.3ex-}_{\text {pump}}\) as a function of the water velocity in the channel, \(V_{\text {water}}\), when the tension in the tether is zero, i.e. \(\dot{V\kern-0.8em\raise0.3ex-}_{\text {pump}} = f\left(V_{\text {water}} \right)\).

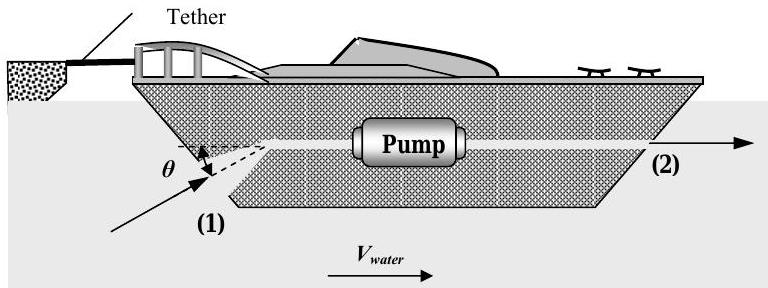
Figure \(\PageIndex{24}\): Water enters a ship to be pumped out the other side.

Problem \(5.33\)

A \(10 \mathrm{-kg}\) steel sphere is suspended from a \(15 \mathrm{-kg}\) frame, and the sphere-frame combination slides down a \(20^{\circ}\) incline as shown in the figure. The coefficient of kinetic friction between the frame and the incline is \(\mu_{\mathrm{k}}=0.15\).

Determine the tension in each of the supporting wires, in Newtons.

Figure \(\PageIndex{25}\): A sphere suspended in a rectangular frame by two cables slides down an incline.

Problem \(5.34\)

You have been hired by NASCAR to analyze vehicle impacts into the wall. For the crash below, solve for the average reactions (\(R_{x, \text { avg}}\) and \(R_{y, \text { avg}}\)) of the wall on the car in terms of the mass of the vehicle \(m\), the initial velocity \(V_{1}\), the angle \(\theta\), the distances \(h\) and \(d\), and the time interval \(\Delta t=t_{2} - t_{l}\) assuming the vehicle comes to a complete stop during the time interval.

Feel free to assume that the car remains a rectangle during the impact.

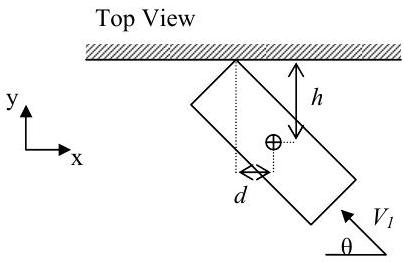
Figure \(\PageIndex{26}\): Top-down view of a car moving towards a wall.

Problem \(5.35\)

Blocks \(A\) and \(B\) are identical and each have a mass of \(10 \mathrm{~kg}\). Block \(B\) is at rest when it is hit by block \(A\), which is moving with velocity \(V_{\mathrm{A}}=6 \mathrm{~m} / \mathrm{s}\) just before impact. Blocks \(A\) and \(B\) stick together after the impact, and you may neglect friction during the impact.

After the impact, the velocity of blocks \(A\) and \(B\) decreases due to friction. The coefficient of kinetic friction between all surfaces is \(\mu_{\mathrm{k}}=0.20\).

(a) Determine the velocity of block \(A\) and \(B\) immediately after \(A\) hits \(B\).

(b) Determine the impulse of the force of block \(A\) on block \(B\) during the impact.

(c) Determine the time required for the velocity of the blocks to drop to \(1 \mathrm{~m} / \mathrm{s}\).

(d) Determine the distance traveled by the blocks during this time interval.

Figure \(\PageIndex{27}\): Behavior of blocks before and after impact.

Problem \(5.36\)

A piece of wood is held at rest on the smooth (frictionless) inclined plane by the stop block at \(A\). A bullet is traveling as shown in the figure with velocity \(V\) when it becomes embedded in the block. The embedding takes a short time, \(\Delta t\). The mass of the wood is \(m_{w}\), the mass of the bullet is \(m_{\mathbf{B}}\), the angle of the inclined plane is \(\theta\), and the acceleration due to gravity is \(g\).

Provide symbolic solutions to answer the following questions:

(a) What is the velocity \(V_{a}\) of the bullet/wood immediately after the bullet becomes embedded? SET UP BUT DO NOT SOLVE. Clearly show how you would use your equations to solve for \(V_{a}\)

For the remaining questions, you may assume that \(V_{a}\) is known.

(b) What is the average impulsive force acting on the bullet during the impact?

(c) What is the equation for the rate of change of velocity of the bullet/wood after the impact?

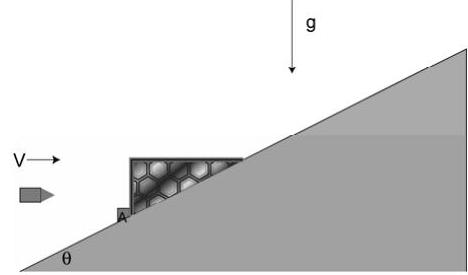
Figure \(\PageIndex{28}\): Bullet approaches a wooden wedge held in place on a ramp.

Problem \(5.37\)

Salt water \(\left( \rho=1025 \mathrm{~kg} / \mathrm{m}^{3}\right)\) enters a vertical pipe at a volumetric flow rate of \(0.5 \mathrm{~m}^{3} / \mathrm{s}\) and is discharged into the atmosphere from the two \(30^{\circ}\) outlets as shown in the figure. The flow divides equally between the two outlets.

Each of the discharge nozzles has an outlet diameter of \(10.0 \mathrm{~cm}\) and the inside diameter of the pipe at section \(A \text{-} A\) is \(25 \mathrm{~cm}\). The pressure of the water at section \(A \text{-} A\) is \(550 \ \mathrm{kPa}\) and the atmospheric pressure is \(100 \ \mathrm{kPa}\). The pipe above the flange and the water within it has a mass of \(60 \mathrm{~kg}\).

Determine the total force exerted by the lower pipe on the section of pipe above the flange \(A \text{-} A\). Indicate both its magnitude, in Newtons, and its direction.

Figure \(\PageIndex{29}\): Salt water flows up a vertical pipe and out of two angled nozzles.

Problem \(5.38\)

A jet engine with exhaust nozzle is mounted on a test stand as shown in the figure. The engine is mounted as shown on two hangars and a diagonal brace. All connections are with frictionless pinned joints.

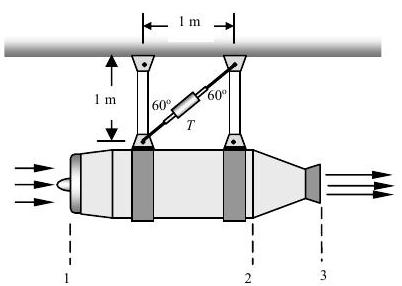
Figure \(\PageIndex{30}\): A jet engine hangs from a test stand composed of three struts.

Information about the flow area, pressure, and air velocity at three locations along the engine are given in the table. At steady-state operation, air is sucked into the inlet at the rate of \(30 \mathrm{~kg} / \mathrm{s}\).

Determine the direction and the magnitude of the force \(T\) in the diagonal brace. Is the brace in tension or compression?

		Sec. 1	Sec. 2	Sec. 3
Flow area	\(\mathrm{m}^{2}\)	\(0.15\)	\(0.16\)	\(0.06\)
Pressure	\(\mathrm{kPa}\)	\(84\)	\(240\)	\(114\)
Air velocity	\(\mathrm{m} / \mathrm{s}\)	\(120\)	\(315\)	\(600\)

Problem \(5.39\)

A bullet strikes and glances off a flat plate as shown in the figure. The plate is resting on a frictionless horizontal surface. Initially, the bullet has a velocity of \(800 \ \mathrm{ft} / \mathrm{s}\) and the plate is stationary. After striking the plate, the bullet velocity is \(600 \ \mathrm{ft} / \mathrm{s}\).

Determine the final velocity of the plate. \[\begin{aligned} &m_{\text {Bullet }}=0.05 \ \mathrm{lbm} \\ &m_{\text {Plate }}=3 \ \mathrm{lbm} \end{aligned} \nonumber \]

Figure \(\PageIndex{31}\): A bullet strikes a flat plate at an angle and glances off.

Problem \(5.40\)

A truck is traveling down a long steady grade \(\left(\theta=15^{\circ}\right)\) as shown in the figure. The crate has mass \(m_{\text {Crate}} =500 \mathrm{~kg}\) with height \(H=1 \mathrm{~m}\) and length \(L=2 \mathrm{~m}\). The crate rests on the trailer bed and the surface has a static friction coefficient \(\mu_{\mathrm{S}}=0.4\) and a kinetic friction coefficient \(\mu_{\mathrm{K}}=0.3\). To prevent the load from shifting, the driver must limit his braking.

Determine the maximum possible truck deceleration if the crate does not slide on the trailer bed.

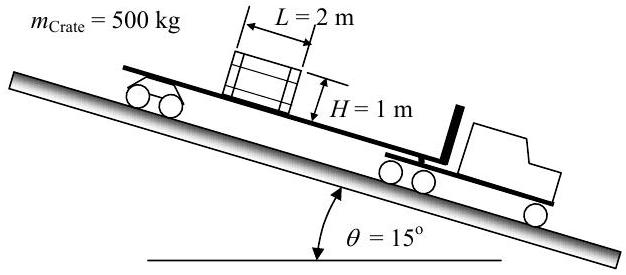
Figure \(\PageIndex{32}\): A truck carrying a crate on its bed travels down a steady grade.

Problem \(5.41\)

Two blocks rest on an inclined plane with \(\theta=35^{\circ}\) as shown in the figure. Block \(A\) has mass \(m_{A}=13.5 \mathrm{~kg}\) and block \(B\) has mass \(m_{B}=40 \mathrm{~kg}\). The coefficients of static and kinetic friction between all surfaces are \(\mu_{S}=0.3\) and \(\mu_{k}=0.2\), respectively. Initially the blocks are stationary and are supported by a stop block and fixed-length wire, as shown on the figure.

When the stop block is removed the block \(B\) immediately starts to move because the angle \(\theta\) is large enough to produce motion.

Find the acceleration of block \(B\) and the tension in the wire immediately after the stop block is removed.

Figure \(\PageIndex{33}\): Blocks stacked on an incline are held stationary by a stop block and a wire attached to a support.

Problem \(5.42\)

The convertible shown is moving at a constant velocity, \(\mathrm{v}_{\mathrm{c}}\), in the direction shown. At the instant shown a passenger in the car throws a ball from the car. The magnitude and direction of the initial velocity of the ball with respect to the car, \(\mathrm{v}_{0}\), is shown in the figure. The ball hits the ground \(30 \ \mathrm{ft}\) to the right of the point from which it was released.

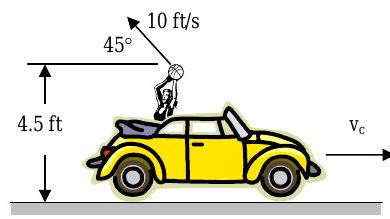
Figure \(\PageIndex{34}\): A car passenger throws a ball upwards and opposite the direction's car of travel.

a) How long does it take the ball to hit the ground from the moment it is released?

b) What is the velocity of the car?

Problem \(5.43\)

The cart has mass \(\mathrm{M}\) and holds water that has a mass \(m_{0}\). If a pump ejects water through a nozzle having a cross-sectional area \(\mathrm{A}\) at a constant rate of \(\mathrm{v}_{0}\) relative to the cart, determine the velocity of the cart as a function of time. What is the maximum speed developed by the cart assuming all the water can be pumped out? Assume the frictional resistance to forward motion is \(\mathrm{F}\) and the density of water is \(\rho\).

Figure \(\PageIndex{35}\): Water on a moving cart is steadily pumped off the cart.

Problem \(5.44\)

Two swimmers \(A\) and \(B\), of mass \(75 \mathrm{~kg}\) and \(50 \mathrm{~kg}\), respectively, dive off the end of a \(200 \text{-kg}\) boat. Each swimmer has a relative horizontal velocity of \(3 \mathrm{~m} / \mathrm{s}\) when leaving the boat. If the boat is initially at rest, determine its final velocity, assuming that (a) the two swimmers dive simultaneously, (b) swimmer \(A\) dives first, (c) swimmer \(B\) dives first.

Figure \(\PageIndex{36}\): Two swimmers line up to dive off the end of a boat.