2.1: System, Property, State, and Process
- Page ID
- 81477
To provide a concrete example for the discussions to follow, let's consider the following problem:

Figure \(\PageIndex{1}\): Problem -- A little girl is playing with a red balloon. Suddenly the string around the neck of the balloon becomes untied and the air begins to rush from the balloon. What is the path of the balloon?
To apply the accounting concept to model the balloon and predict its motion, we must first answer three questions:
- What property (or properties) do we want to count?
- What's the system we want to examine?
- What's the time period of interest?
These three questions should be answered each time we apply the accounting concept. But before we can answer the questions, we need to introduce some terms and concepts.
As a starting point for our discussion, we will begin to develop a vocabulary for describing the behavior of physical systems. These words sound familiar, but be sure that you understand the definitions given here for these terms.
2.1.1 System
The accounting concept can only be applied to a system. So what's a system? A system is any region in space or quantity of matter set aside for analysis. In the balloon problem, there are at least four possible systems:
- System A - the mass of air originally inside the balloon when the string comes untied,
- System B - the volume contained inside the balloon,
- System C - the balloon (just the rubber membrane), and
- System D - the balloon (System C) plus the volume contained inside the balloon (System B).
Notice that System D is really a composite system formed by combining System B and System C. That is, System B and System C are subsystems of System D.
Once you have defined your system, you have also defined the surroundings. The surroundings are everything outside of your system. The system and its surroundings are separated by the system boundary. In some texts, the system boundary is also called a control surface. Figure \(\PageIndex{2}\) shows a sketch of a generic system with the system boundary indicated as a dashed line. This is common practice in sketching systems.
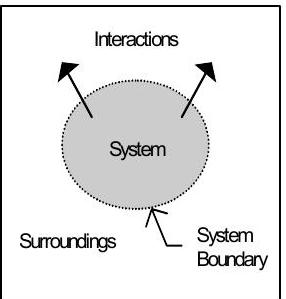
Figure \(\PageIndex{2}\): A simple system sketch.
Control surfaces may coincide with a real, physical boundary in the problem, or they may be imaginary surfaces in space. Imagine your room as a system. If you treat the door opening as a control surface, the surface may be real if it coincides with a shut solid door; however, if the door is open then you might describe the surface as being imaginary.
Every system can be classified as either open or closed. A closed system is a system with a fixed quantity of mass, and is often called a control mass. An open system is a system with a specified volume and is frequently referred to as a control volume. The mass of a closed system cannot change; however, other extensive properties including its volume may change. Both the mass and the volume of an open system may change.
Let's return to the balloon problem and classify the four systems we identified earlier:
- System A - the air originally inside the balloon when the string comes untied.
This is a closed system because we have identified the mass as the system. To better visualize how this system will behave as time proceeds imagine that all of the air initially in the balloon is stained green. Then imagine what this air looks like as the balloon zooms around and leaves a trail of "green" air. The system boundary (or control surface) would be the sharp interface between the stained and unstained air.
- System B - the volume contained inside the balloon.
This is an open system because we have identified a region of volume as the system. In this system, the system boundary consists of the inner surface of the balloon membrane and the imaginary surface that covers the opening at the neck of the balloon. The air rushing out of the balloon passes out of this system and the control volume will shrink in size as the balloon deflates. Although we have defined the system in terms of a volume, the mass of air contained in the volume is also in the system and as the balloon deflates the amount of mass in this system decreases.
- System C - the balloon (just the rubber membrane).
This is also a closed system. Why isn't it an open system? Does the mass of the system change? Does the volume of the system change?
- System D - the balloon plus the volume contained inside the balloon.
The boundary of this system consists of the outer surface of the balloon and an imaginary surface that covers the opening at the neck of the balloon.
To test your understanding try to answer the following questions about System D:
- Is System D an open or closed system? Why?
- Does its mass change? Does its volume change?
- How does the system boundary of System D differ from that of System B?
- To better understand the distinctions between systems, resketch the balloon and identify (draw) all four systems below. Use dashed lines to indicate the control surfaces.
Typically a system interacts with its surroundings in various ways. We will refer to any exchange (or communication) between a system and its surroundings as an interaction. Interactions occur across the boundary of a system and are represented as arrows on Figure \(\PageIndex{2}\). The interactions that can occur depend on both the system you have selected and the physical description of the problem. Without interactions, system behavior would be pretty boring. Much of our effort this quarter will be aimed at learning how to make modeling assumptions that capture the important features of the interactions in a problem.
Using a dashed line, sketch a system that encloses the light bulb and cuts the electric cord.
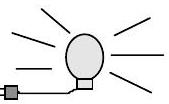
Figure \(\PageIndex{3}\): Sketch of a light bulb
(a) Is this an open or closed system?
(b) List all the interactions that occur between this system and its surroundings.
There is one very special type of system that has no interactions with its surroundings. We call this an isolated system. It is physically impossible to construct a system that is completely isolated from its surroundings; however, it is often a useful approximation (assumption) for modeling purposes. If you assume that a system is isolated, you are assuming that it has NO interactions of any kind with the surroundings. This is a very powerful assumption and places a severe restriction on the behavior of a system.
2.1.2 Property
Every system has many characteristics that we could use to describe it. We are specifically interested in characteristics that can be measured by observing the system or can be calculated directly from these observations. These are called properties. A property is any characteristic of a system that can be assigned a numerical value at a specified time without considering the history of the system.
Now consider the air inside our balloon just before it starts to zoom around. How many different properties of the system could you list? After some thought, your list might look like this:
|
|
All of these are properties of the air in the system. Now examine the two lists. What's different about the two lists? Any ideas?
What are the three key characteristics of a property?
1)
2)
3)
It turns out that the list on the properties on the left are all intensive properties and the properties on the right are extensive properties. An intensive property is independent of the extent of the system and has a value at a point. By contrast an extensive property depends upon the extent of the system and cannot be evaluated at a point. Some intensive properties have an extensive counterpart; these are called specific properties.
Again consider the air in the balloon. The mass of the air in the balloon can be thought of as the sum of all of the individual masses within the balloon. The temperature on the other hand cannot be thought of in the same way. Extensive properties are additive, but intensive properties are not.
2.1.3 State
The state of a system is a complete description of the system in terms of its properties. When we attempt to describe the condition of a physical device, we are actually trying to specify its state.
Strictly speaking, the state of a system can only be known when all of its properties are known. Luckily, we will find that under many conditions only a few properties must be known to specify the state sufficiently for our analysis. In addition, we will learn that many properties are related to each other. For instance, the pressure, temperature, and density of a gas at room conditions are related by something called the ideal gas model, and you need only specify two of these properties to uniquely fix the value of the third property.
2.1.4 Process
As a system interacts with its surroundings its properties may change, and when they do, we say that it has changed state or undergone a process. Without processes, our study of engineering systems would be pretty simple—nothing changes. During the quarter we will examine many different processes and how systems change.
There are two processes that merit special attention because they are so common in nature—a cyclic process and a steady-state process. A cycle is a sequence of processes that, combined, begin and end at the same state. The operation of many important engineering systems can often be modeled as a periodic cycle. Examples of this type of system include the refrigerator in your house and the engine of your car.
A steady-state process is a process in which the intensive properties of a system and it interactions are independent of time. Many real devices can be modeled using the steady-state assumption. Instead of talking about a steady-state process, we will often talk about a steady-state system. We will take these two expressions—steady-state process and steady-state system—as being synonymous. This is a very powerful assumption, and where applicable we will use it to remove time as a variable from our analysis.
2.1.5 Properties and Processes — A Test
Recall that we defined a property as any characteristic of a system that can be assigned a numerical value without knowing the history of the system. Another way of saying this is that the value of a property only depends upon the state of the system. If a system undergoes a process between two specified end states, the change in any property of the system is solely a function of the end states and is independent of the history of the system.
This result provides us with a useful test for determining if something is a property or not:
If the change in the value of a system characteristic between two end states is independent of the process, then the characteristic is a property.
Properties are sometimes called point or state functions because of this functional dependence on the state of the system.
We will see later that there are many physical quantities that are not properties because their value depends upon knowing the path of the process. One important class of these is system interactions. We will learn to call these quantities path functions.


