4.4: Ohm's "Law" -- A Constitutive Relation
- Page ID
- 81491
One of the most frequently used constitutive relationships in studying electrical phenomena is referred to as Ohm's Law. This, like every constitutive relationship, is not really a law but a well-worn and useful model for a specific physical phenomenon.
Ohm's Law relates three circuit variables: current, voltage, and resistance. For purposes of our discussion here, we will define voltage at a point \(\mathrm{A}\) with respect to a reference point \(\mathrm{N}\) as the value read by a "voltmeter" connected between the two points. The voltage at point \(A\) will be given the symbol \(V_{\mathrm{AN}}\) to remind us that every voltage reading is always measured with respect to some reference, e.g. point \(\mathrm{N}\). A typical system is shown in Figure \(\PageIndex{1}\).
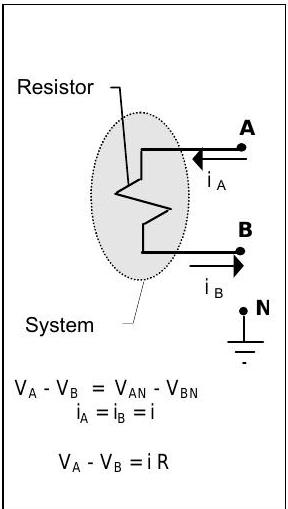
Figure \(\PageIndex{1}\): A system consisting of a resistor within a physical circuit.
Empirical evidence for lumped circuit resistors shows that (1) there is no accumulation of charge in the resistor and (2) the current flowing through the resistor is related to the voltage change across a resistor by the following equation:
\[V_{\mathrm{AN}} - V_{\mathrm{BN}} = iR \nonumber \]
where
- \(V_{A N}\) is the voltage at point A measured with reference to ground N, in volts
- \(V_{B N}\) is the voltage at point B measured with reference to ground N, in volts
- \(i\) is the electrical current flowing from point A \(\rightarrow\) B, in amperes
- \(R\) is the electrical resistance, in ohms where \(1\, \text{volt} = (1 \mathrm{~A}) \times (1 \mathrm{\ ohm})\)
Equation \(\PageIndex{1}\) is known as Ohm's Law and the various terms in the equation are shown in Figure \(\PageIndex{1}\). In a resistor, the magnitude of the voltage always decreases in the direction of the current flow, i.e. current flows inside a resistor from a high voltage to a lower voltage.


