14.11.1: Statics
- Page ID
- 45674
 |
| Original columns that held up the capitol dome now located in the National Arboretum, Washington DC. Holding up the capitol dome would be a statics problem in mechanics. |
Statics
Statics is the study of objects under different forces when the body is at rest in equilibrium. From an equation point of view this means that the sum of forces are equal to zero and the sum of moments (negative torque1, see description in vectors) are equal to zero. Assuming that we are in a rectangular coordinate system, the vectors have been decomposed to summable parts, and we have an object that has two pivot points (A and B) we can write the equations that define a static situation as the following:
\[\sum F_x = 0 \qquad \sum F_y = 0 \qquad \sum F_z = 0\]
and
\[\sum M_A = 0 \qquad \sum M_B = 0\]
When moment is involved one of the biggest hurdle for students is what defines a pivot point. Below, we present three examples in the hopes of helping the student with this hurdle.
Procedure
First let us establish rules for solving problems in mechanics when dealing with forces (these are the same rules in physics class).
- First step is to draw your coordinate directions (which way does "x" go...which way does "y" go...which way does "z" go). Note if there is just one dimension then just use one coordinate, etc.
- Second step is to set up your force and moment diagram.
- Third step is depending on the situation get the component parts of the various forces.
- Forth step is to establish the force and moment equations.
- Fifth step is to use your statics equations (or dynamics equations).
An important idea that is always used in engineering class but is only sometimes used in physics class, is the idea of a distributed load. A distributed load (units N/m) is like a one dimensional pressure2. The figures below represent a simple expression of distributed load and a more complex expression of distributed load. The idea is that the forces are not pin-point but instead distributed throughout a system. A good way to think about this is ice on an airplane wing. Ice on a wing is likely to have different forces at different points which we can represent using a distributed load. We won't go into that much detail on this (as this would eventually lead to some form of finite element analysis which is beyond this course). We will just introduce the concept and do simple examples (which are not as good as doing this correctly, but are good for conceptual understanding).
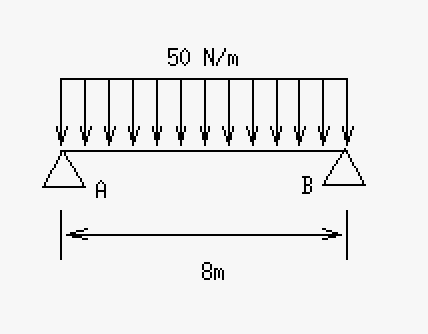 |
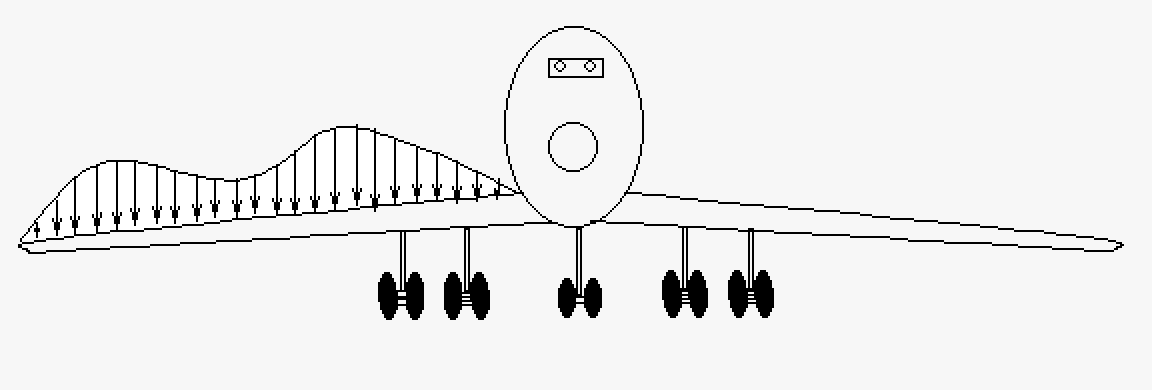 |
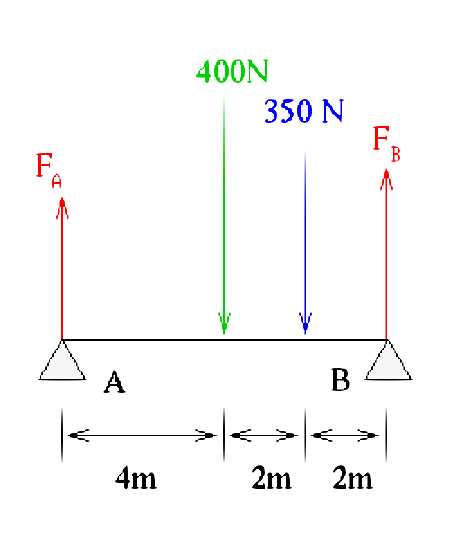
| This is the simplest example of a distributed load. As a rectangle with uniform load this can be converted to a "single-point" force by using the center of mass3 (which we will call the distributed load force herein). In this example we could replace the load with a force of 400 N centered between points A and B (4 meters in from either point). | This is a more complex example of a distributed load. This is a cartoon of an airplane with its wing covered in a combination of snow and ice. In a real world situation loads will not accommodate people for ease of calculation, you get what you get. In this case we could approximate this shape with two semi-circles on each end of the wing with a triangle (\(\nabla\)) in the middle. For more accuracy we could use a system similar to the trapezoidal rule. |
Example 1
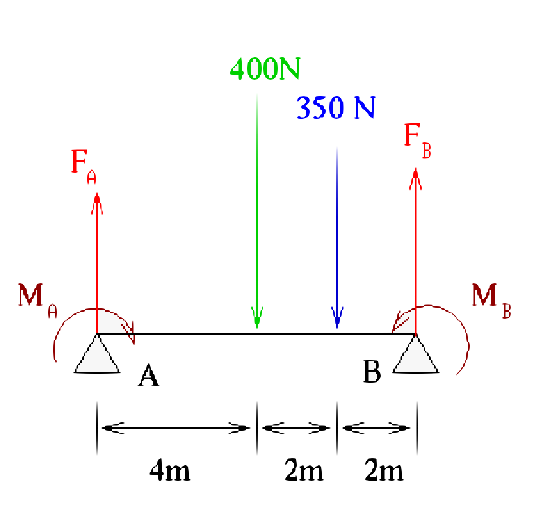
Calculate the reactive force at support B pictured in the figure below.
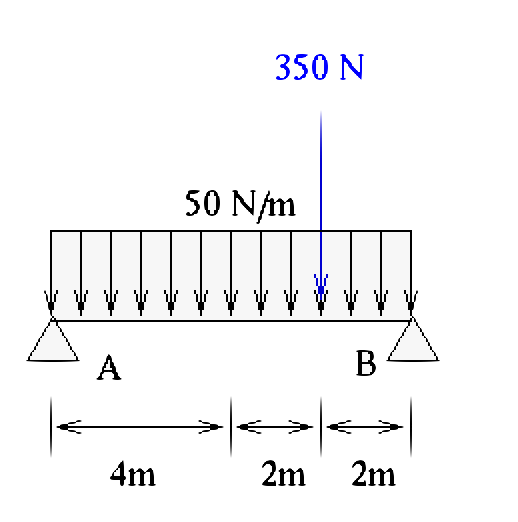
Solving a distributed load problem
We are given a problem above that has a distributed load along with a single force applied at one point, so how do we solve this?
The distributed load is 50 N/m which you could envision as a one dimensional pressure along the beam. The single force point is 350 N.
Let us figure out the reaction force at B. First let us convert the distributed load into a single force \(F_D\) at its center of mass (we can do this for this problem rather easily, but it may not be so easy for other problems). \(F_D = (50 \frac{N}{m})(8m) = 400 N\) which will be placed (centered) at 4 m. The forces are shown below for this particular problem (force diagram - always do that first). Since reaction force is up in this figure we will assume the coordinate system (say y) will be up as well so the reaction forces are positive.
Since the system is static we consider the following four equations for this problem:
\[\sum{F_x} = 0 \qquad \sum{F_y} = 0 \qquad \sum{M_A} = 0 \qquad \sum{M_B} = 0\]
The sum of the forces must be equal to zero (or the problem is not be static). Since we said we will use the y-direction for up then the second force equation is all we need to consider in this problem. This gives us
\[F_A + F_B - 400 - 350 = 0\]
This gives us the reaction force of B in terms of A. However we do not have another force equation to be able to solve this (one equation, two unknowns is not useful, of course). But we can look at the moment about A. Why A and not B? Because B has the reaction force itself which will not be involved in the moment about B. For moment we have \(M = F \times \textrm{distance}\).
The moment about A is then
\[F_B \times 8 - 350 \times 6 - 400 \times 4 = 0\]
\[8F_B = 3700\]
\[F_B = 462.5 \ N\]
You might note that this makes sense from just a thought experiment point of view where all the forces are divided up with appropriate "weights" to "equalize" the reaction forces. The forces with the moments are shown below.
Example 2
Another distributed load problem
Calculate the reactive force at support B pictured in the figure below. Try to solve this on your own first. You will have to think about it.

- ¬ Force and moment diagram (with coordinate system)
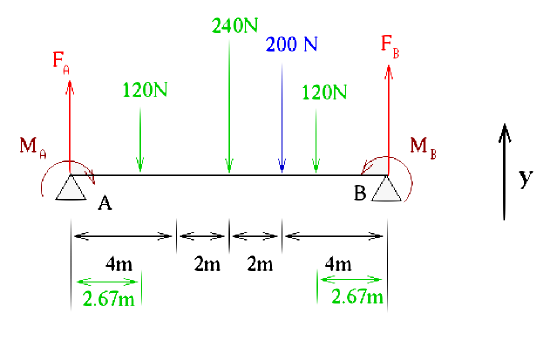
- Here we have the center of mass forces based off the distributed load in green, plus were they are placed in the diagram. Also the moments are shown. The forces and positions are calculated based off the shape of the portion of the distributed load.
- ¬ Forces and moments defined
- The key here is to take the distributed load and break it up into areas that we can get the center of mass force and placement. Note that if we were figuring out the area of the distributed load above we would split it up to a two triangles and a rectangle. Well that simple arithmetic way of getting area is exactly what we do for the center of mass force. So there are three center of mass forces, one a rectangle which is \(F_{rect} = 60 \frac{N}{m} \times 4 \ m = 240 \ N\), and two triangles that have the same center of mass force which is \(F_{\Delta} = \frac{1}{2} \times 60 \frac{N}{m} \times 4 \ m = 120 \ N\). Now that we have the values we need to know where to place them. The rectangle is the easiest as that should be right at the center of the rectangle or 6 m from support A (or B). The triangles should be at a distance that would represent the center of gravity (where to place the triangle on your figure so it will balance) which is \(\frac{1}{3}\) the distance from the right angle vertex (in the x-direction). Therefore one of the forces should be place 2.67 m from support A and one 2.67 m from support B. This is reflected in the previous figure.
- ¬ Solution
-
Since this is a statics problem we establish the following equations.
\[\sum{F_y} = 0 \qquad \sum{M_A} = 0 \qquad \sum{M_B} = 0\]
For force equation it is clear we will have \(F_A + F_B - 120 -240 - 200 - 120 = 0\) which has two unknowns with only one equation, so we should look to the moment equations to solve this. Since we want the reaction force on support B we would use the moment equation for support A.
\[F_B \times 12 - 120 \times 9\frac{1}{3} -200 \times 8 - 240 \times 6 - 120 \times 2\frac{2}{3} = 0\]
\[12F_B = 4480\]
\[F_B = 373\frac{1}{3} \ N \qquad \checkmark\]
Example 3
A different type of problem
An ice skater had a bit of a spill and sprained her ankle. The doctor decided that the leg needed to be raised a bit to enhance healing. What mass would be needed to suspend her leg in a simple pulley configuration described in the figure? The skater weighs 60 kg and the average percentage weight of a leg is about 18% of the total weight of a person. The center of mass (CM) is about 26 cm from the hip rotator cuff and the ankle support is about 73 cm from the hip rotator cuff.
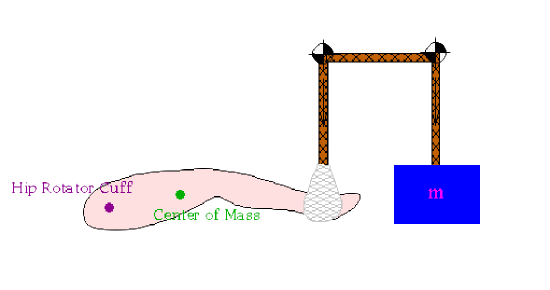
- ¬ Force and moment diagram (with coordinate system)

- Here we have gravitational forces and tension forces. Also there is a moment about the hip rotator cuff.
- ¬ Forces and moments defined
- In order to solve this problem we need to note that this is a statics problem as there is no motion (the leg is suspended not being picked up). Only one force needs to be defined and that is \(F = mg\).
- ¬ Solution
-
Since this is a statics problem we use the following equations.
\[\sum{F_m} = 0 \qquad \sum{M_H} = 0\]
Which leads to
\[F_g - F_T = 0\]
\[F_g = F_T\]
Noting that the tension is the same on both sides of the pulley system we can utilize the moment equation.
\[0.26 F_{cm} - 0.73 F_T = 0\]
\[0.26 F_{cm} - 0.73 F_g = 0\]
\[0.26 m_{cm}g = 0.73 mg\]
\[m = \frac{0.26}{0.73} m_{cm}\]
The center of mass needs to be calculated as it is not given as a single number. It is a simple problem in itself.
\[m_{cm} = 0.18 \times 60 = 10.8 \ kg\]
Plugging the center of mass in gives us the solution to the problem.
\[m = 3.8 \ kg \qquad \checkmark\]
Next we consider dynamics.
1Torque and moment in physics are considered to be the same thing, but in mechanical engineering they are the opposite of each other. That is \(\vec{M} = \vec{F} \times \vec{r} \rightarrow Fr\) and \(\vec{\tau} = \vec{r} \times \vec{F} \rightarrow rF\). The reason behind this is because of how each discipline uses the moment (it is more particular to mechanical engineering). There are differences between physics, mathematics, and engineering sometimes that amount to just a small thing (like one being the negative of another) so you need to be careful in what discipline you are talking in.
2Pressure has units of \(\frac{N}{m^2}\) which is force per area whereas a distributed load would be force per length. Stress, shear stress, and strain have the same units of pressure. While the units are the same the ideas are different with pressure being external force and stress and strain being internal. For completeness a pressure gradient \(-\vec{\nabla} P\) would have units of \(\frac{N}{m^3}\). Pressure gradients are normally used in fluid mechanics (Cauchy momentum equation or Navier-Stokes momentum equation which are used in advanced classes though might be used in a simpler form in computer class).
3Center-of-mass and center-of-gravity are two different concepts that are equal in most situations.