14.11.2.1: Kinematics
- Page ID
- 45685
Kinematics describes the motion of objects without reference to force. Specifically, kinematics means the science of motion and is derived from the same Greek word that gives us cinematic (cinema - which is pictures in motion, so makes sense, eh?). Here we discuss the very basics of kinematics to give a starting idea of what it is about.
We start with the idea that we have a length (in vector form that represents the three elements to define a point in 3D space).
\[\vec{x} = \left(\array{x_1 \\ x_2 \\ x_3}\right)\]
where here we can take x1, x2, and x3 to be x, y, and z if we wish. From here on we will use the traditional \(\vec{s}\) rather than \(\vec{x}\) as it is more general.
Linear World
To get velocity we take the derivative.
\[\vec{v} = \frac{d\vec{s}}{dt}\]
To get acceleration we take the derivative again.
\[\vec{a} = \frac{d\vec{v}}{dt} = \frac{d\vec{s}^2}{dt^2} = \vec{v}\frac{d\vec{v}}{ds}\]
To continue this though process, for the derivative of acceleration we get jerk, the derivative of jerk gets snap, the derivative of snap gets crackle, the derivative of crackle gets pop, etc. While jerk, snap, crackle, and pop are important in real world engineering and physics we will not discuss them here except for brief mentions; feel free to learn about them yourself.
From these initial equations and the assumption that acceleration is constant we can produce the important kinematic equations by integrating the various initial equations above
\[v = v_0 + at\]
\[s = s_0 + v_o t + \frac{at^2}{2}\]
\[v^2 = v_0^2 + 2 a (s-s_0)\]
It is possible to produce kinematic equations with non-constant acceleration, but those would be in terms of constant jerk (or snap or crackle or pop). Just follow the same principle of integration, but instead use jerk (or snap or crackle or pop). Are these useful? Yes, in real life we do have jerk, etc. so we might want different kinematic equations.
Angular World
To get angular velocity we take the derivative of the angular "length".
\[\vec{\omega} = \frac{d\vec{\theta}}{dt}\]
To get angular acceleration we take the derivative again.
\[\vec{\alpha} = \frac{d\vec{\omega}}{dt} = \frac{d\vec{\theta}^2}{dt^2} = \vec{\omega}\frac{d\vec{\omega}}{d\theta}\]
To continue this though process, for the derivative of angular acceleration we get angular jerk, the derivative of angular jerk gets angular snap, the derivative of angular snap gets angular crackle, the derivative of angular crackle gets angular pop, etc. Again these are important in the "real world," but they are fairly advanced and are best studied much later in your academic career.
From these initial equations and the assumption that angular acceleration is constant we can produce the important angular kinematic equations by integrating the various initial equations above
\[\omega = \omega_0 + \alpha t\]
\[\theta = \theta_0 + \omega_o t + \frac{\alpha t^2}{2}\]
\[\omega^2 = \omega_0^2 + 2 \alpha (\theta-\theta_0)\]
It is possible to produce kinematic equations with non-constant angular acceleration by following the same idea as in the linear world mini-section.
Linear and angular world
In general the linear and angular world are tethered together. We saw this in statics in considering both the sum of forces and sum of moments in the examples. In kinematics there are equations the incorporate both concepts. We find there use especially relevant in orbits of planetary object. Here we will point out the basic "first principle" equations. But note that since we are talking circular motion we will need to employ the cross product (see vector section).
\[\vec{v_n} = 0\]
\[\vec{v_t} = \vec{\omega} \times \vec{r} = \vec{v}\]
\[\vec{a} = \vec{a_t} + \vec{a_n}\]
\[\vec{a}= \frac{d\vec{v}}{dt} = \frac{d(\vec{\omega} \times \vec{r})}{dt} = \vec{r} \times \frac{d\vec{\omega}}{dt} + \vec{\omega} \times \frac{d\vec{r}}{dt} = \vec{r} \times \vec{\alpha} + \vec{\omega} \times \vec{v} \]
\[\vec{a_t} = \vec{r} \times \vec{\alpha}\]
\[\vec{a_n} = \vec{\omega} \times \vec{v} \]
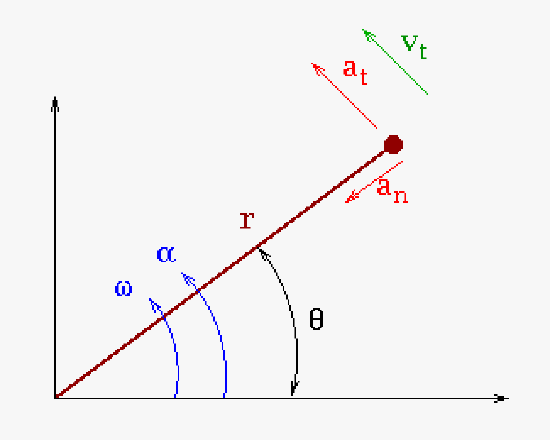 |
| Cartoon description of the relationship between the linear and angular world. The subscript t indicates tangential motion and the subscript n indicates normal motion. Note the normal acceleration is sometimes referred to as centripetal acceleration. In physics class the centrifugal force1 and the gravitational force (which some refer to as centripetal force though this is more Newtonian rather than Einsteinian) are used to explain the stability of orbits, though this is not exactly true with real orbits for a number of reasons it is a very good approximation. Sometimes the tangential velocity and centripetal acceleration is used to explain the stability of the orbits: that description is more visually satisfying and allows for a better understanding of the stability of orbits. |
Giving a right angle between \(\vec{a_t}\) and \(\vec{a_n}\) in the circular orbit normally introduced in physics class we can just express the equations more simply as
\[v_t = r \omega = v\]
\[a_t = r \alpha = \frac{dv}{dt}\]
\[a_n = r \omega^2 = \frac{v^2}{r}\]
Simple harmonic motion can also have an expression combining the linear world with the angular world.
\[a = \frac{dv}{dt} = -\omega^2 r\]
This is useful in simple simulations were simple harmonic to represent the motion of molecules (or atoms).
This is all that is going to be said for this brief introduction, a simple example (good for a test question) will be given then we will go onto kinetics.
Example
The example for this section will not involve the angular portion (we will save that for your physics class).
Consider an idealized projectile motion on Mars. Find expressions (equations) for the range L and the maximum height H in terms of the initial velocity v0 and angle \(\theta\).
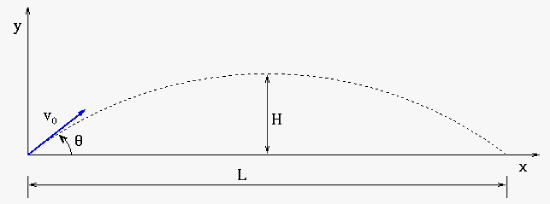 |
| Some visual aid for the problem stated herein. The blue area represents the projectile that has originally launched with a velocity of \(v_0\). Of course real world effects (wind and the acceleration to get to the initial velocity could be added to make this problem even more interesting, however the result won't be that different from this example unless we are talking about very strong winds). |
Answer
We start with the two kinematic equations
\[s_x = s_{0x} + v_{0x}t + \frac{1}{2} a_x t^2 \qquad s_y = s_{0y} + v_{0y}t + \frac{1}{2} a_y t^2\]
and we note that \(a_x = 0\) and \(a_y = - 0.377g\). We also need to express the velocity in terms of its components in x and y, therefore \(v_{0x} = v_0 cos(\theta)\) and \(v_{0y} = v_0 sin(\theta)\) which leads to the equations
\[s_x = v_0 cos(\theta) t \qquad s_y = v_0 sin(\theta) t - \frac{0.377gt^2}{2}\]
Notice that \(s_y\) equals 0 at one end and L at the other end. Therefore we can use this to determine the time it takes to get to L by using the \(s_y\) equation which leads to the equation
\[0 = v_0 sin(\theta)t - \frac{0.377 g t^2}{2}\]
which has two solution, \(t=0\) which is trivial and \(t = \frac{2 v_0 sin(\theta)}{0.377g}\). Therefore plugging in our non-trivial t into \(s_x\) when it equal L we get
\[L = v_0 cos(\theta) \frac{2 v_0 sin(\theta)}{0.377 g}\]
\[L = \frac{v_0^2 sin(2\theta)}{0.377g} \qquad \checkmark\]
And plugging in one-half of the time, \(t = \frac{v_0 sin(\theta)}{0.377g}\), to get to L into \(s_y\) and setting it equal to the height, H, we get
\[H = v_0 \left(\frac{v_0 sin(\theta)}{0.377g}\right) - \frac{0.377g}{2} \left(\frac{v_0 sin(\theta)}{0.377g}\right)^2\]
\[H = \frac{1}{2}\left(\frac{v_0^2 sin^2(\theta)}{0.377g}\right) \qquad \checkmark\]
1Centrifugal force is an apparent force like the Coriolis force and are real forces. There is an argument that centrifugal force is not real and fictitious, but this depends on what you call a force (or anything for that matter). Almost all the items we define in physics are a concept and could be said to be not real or real depending on a particular view point (think on this - is mass real? Mass is NOT weight so be careful how you approach this.). There is an argument if you feel it then it is real, therefore reactive centrifugal force (like in a car when you turn) would be real. Coriolis force under this argument is also real. But each of these forces can be reformulated with other "real" forces however this is a circular argument (like saying A+B = C therefore C is not real, but we could say A-C=B therefore B is not real). And if this argument is used then centripetal force is not real as well as it is always another force (like gravity for instance). Actually there is a stronger argument for centripetal force not being real then for centrifugal force and Coriolis force. An attempted fix of this controversy is to just say centrifugal and Coriolis are apparent forces. However if we take a deeper look using frames of reference (graduate level physics) then indeed these forces are real.

