14.11.2.2: Kinetics
- Page ID
- 45691
Kinetics describes the motion of objects with reference to force (and/or moment). Specifically, kinetics means forcing into motion. Here we discuss there very basics of kinetics to give a starting idea of what it is about.
Before moving to force we define linear momentum as \(\vec{p} = m\vec{v}\) and angular momentum as \(\vec{L} = I\vec{\omega}\). Both linear momentum and angular momentum are conserved in an isolated system (conservation laws will be discussed later in this course). Linear momentum ("impetus" which should not be confused with impulse) is a developed concept that is believed to have started with Aristotle, drastically improved by Philoponus (6th century) and by Ibn Sina (9th century, also known as Avicenna; not to be confused with Ibn Sahl), then refined by Buridan (12th century), and reaching its understood from of today by Newton (15th century).1
Kinetics is the study of objects under different forces when the body is not at rest (i.e. dynamic instead of static). From an equation point of view this means that the sum of forces are equal to the time derivative of momentum and the sum of moments are equal to the time derivative of angular momentum.
\[\sum \vec{F} = \frac{d\vec{p}}{dt}\]
and
\[\sum \vec{M} =\frac{d\vec{L}}{dt}\]
If we assume mass is constant and shape is constant then we can rewrite these equations as
\[\sum \vec{F} = m\vec{a}\]
and
\[\sum \vec{M} = I\vec{\alpha}\]
Where I is the moment of inertia (SI units of kg-m2) and is the angular equivalent of mass (m with SI units of kg). Note mass and moment of inertia are not the same.
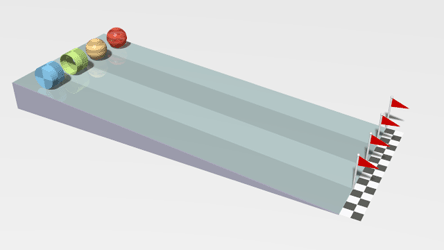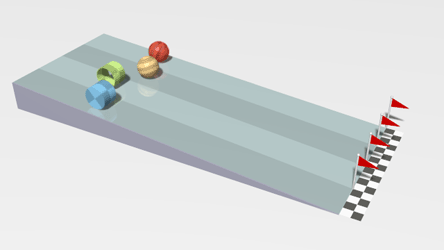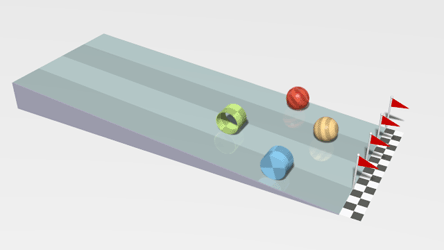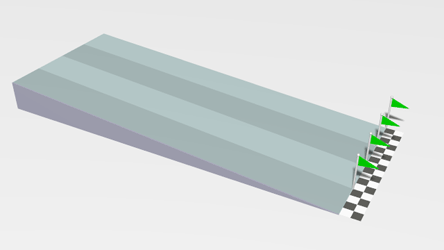 |
| This is a simulation of four objects with the same mass but different moment of inertia. If these balls were sliding down the ramp ("linear world") they would all get to the bottom at the same time, but because they are rolling down the ramp ("angular world") they get to the bottom at different times due to their different moment of inertia. The brownish-yellow ball is a solid sphere which would have the greatest moment of inertia, the blue object is a solid cylinder, the red ball is a spherical shell, and the greenish object is a ring. Note that gravitational force is still dependent on the mass of the objects and not the moment of inertia. The solution to this problem mathematically is easier to do using energy in combination with kinematics rather then the methods presented in this section. From Wikipedia: public domain creation of Lucas Vieira: Rolling racers. |
This section will not discuss the equation that deals with angular momentum as that is more suitable for an advanced course, but some brief remarks will be made for completeness.
Newton's Law of Universal Gravitation
The law of gravitational force is an very accurate approximation of the forces between two bodies. Before Eddington's verification of Einstein's gravitational theories it was believed to be exact and is for all intensive purposes exact in most situations. The law in its modern form between two objects of m1 and m2 is
\[\vec{F_{12}} = \frac{G m_1 m_2}{r_{12}^2}\hat{r_{12}}\]
where G is the universal gravitational constant (SI units of \(6.67 \times 10^{-11} \frac{N m^2}{kg^2}\) and the direction of the force is defined by \(\hat{r_{12}}\).
Newton's laws of motion
- 1st law: An object at rest stays at rest; an object i motion stays in motion assuming no external forces (unbalanced forces)
- 2nd law: Force equals the time derivative of momentum: \(\vec{F} = \frac{d\vec{p}}{dt}\) or where mass is constant \(\vec{F} = m\vec{a}\)
- 3rd law: When two objects interact (say by collision) they have equal, collinear, and opposite reactions
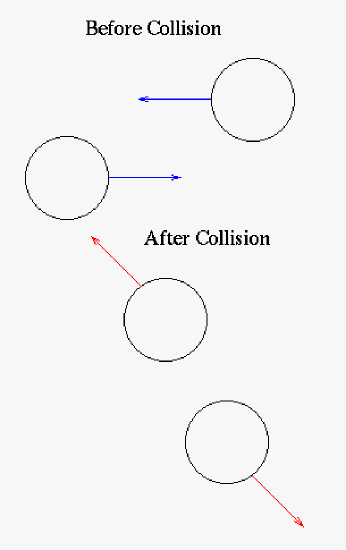 |
| Cartoon of two object colliding to show the collinear reaction portion of Newton's 3rd law. Here two balls glance each other which might happen in planetary interactions. |
So far we have been solving mechanics problems with kinematics and kinetics, but some of these problems can be solved using energy.
Examples
How far does a block slide on a 30 degree inclined plane in t = 10 seconds if the coefficient of friction is \(\mu_k = 0.4\)?
Since the block is moving we recognize this as a dynamic problem, but there maybe more to this problem then what we first observe. At any rate we should always methodically follow the following steps.
- First step is to draw your coordinate directions (which way does "x" go...which way does "y" go).
- Second step in a dynamic physics problem is to set up your force diagram.
- Third step is depending on the situation get the component parts of the various forces.
- Forth step is to establish the force equations.
- Fifth step is to use your dynamics equations (or statics equations).
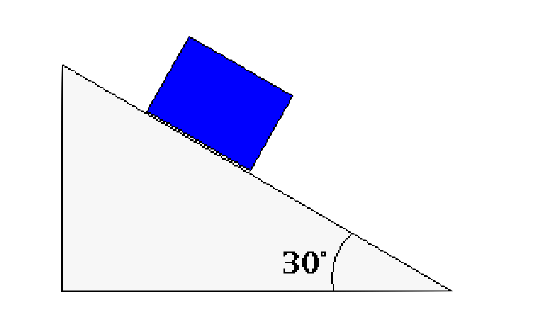
- ¬ Sliding block force diagram (with coordinate system)
-
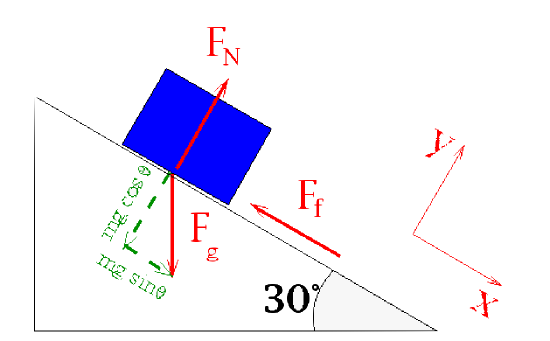
Here the coordinate system is at an angle so that only one force has to be converted into its component parts, x is also going down the ramp as that is the direction the block will go. The forces are \(F_N\) which is the normal force, \(F_f\) which is the sliding friction force (we assume the block is in motion as soon as the problem starts; this is not quite real world, but good enough), and \(F_g\) which is gravitational force which you probably surmised already. The gravitational force is broken up into it's component parts (in green) to better solve the problem. Note that frictional force is proportional to normal force.
- ¬ Forces defined
-
Since we are going to combine forces only in their respective directions we can dispense with the vector notation. We first establish the equation between normal force and frictional force using the coefficient of friction as the proportionality constant.
\[F_f = \mu_k F_N\]
- ¬ Solution
-
Now we have an interesting system here as one part of the problem is static (the y-direction) and one part is dynamic (the x-direction), so following the rules we have established previously we have
\[\sum{F_y} = 0 \qquad \sum{F_x} = ma\]
were we have assumed the mass is constant. This leads to the following two equations
\[F_N - mg cos(\theta) = 0 \qquad mg sin(\theta) - F_f = ma\]
where the gravitational force components have been included in the equations. Solving for the static equation we get
\[F_N = mg cos(\theta)\]
which can be substituted into the second equation with the addition of the frictional force equation
\[mg sin(\theta) - \mu_k mg cos(\theta) = ma\]
\[a = g sin(\theta) - \mu_k g cos(\theta)\]
where it might be noted that the mass was not needed to solve this type of problem (note that the mass is irrelevant in the case of rolling objects, as well, as mass is part of the moment of inertia, however, the shape of the object will matter).
Plugging in the values presented in the initial problem we have \(a = 1.5052 \; \frac{m}{sec^2}\) but this does not solve the problem as we want the distance traveled. Since a is constant we can use one of the kinematic equations.
\[s_x = s_{0x} + v_{0x} + \frac{1}{2} a_x t^2\]
where \(s_{0x}\) and \(v_{0x}\) will be reasonably assumed to equal zero. Plugging in the acceleration and the time we get \(s_x = 75.3 m \quad \checkmark \).
Momentum and Impulse Force (or just Impulse)
Momentum is a property of a body which can be interpreted to mean what force is needed to change a body's motion. An impulse is the change of momentum2 (\(mv_2 - m v_1\) or \(F_{\Delta t} \times \Delta t\)) of a body usually used to describe collision. J is the common symbol for impulse force (because it is not really a force per say as it has units of force-time). The impulse force3 is very useful in problems of collision and quick pushes and pulls of objects (like closing a car door). One problem in engineering is to minimize the impact of impulse force. In order to do this you could reduce the force, but that usually isn't possible in most cases, so increasing the duration of the time is usually where the engineer looks to. Car impacts during a crash are a good example where lengthening the duration of the crash (through crumble zones) actually reduces the impact of the impulse force.
How is change of momentum and impulse force equal? Let us use calculus4 to prove the point, \(J = \int F dt = \int {dp \over dt} dt = \int dp \ dt\) which clearly shows the \(J = \Delta p\). Of course your physics class will go into much more detail on this.
Next we consider hydraulics and its similarity to the latest topics herein.
1There is an argument for others scientists to be the originator of the final form but Newton’s idea of a “quantity of matter” (i.e. mass) it is believed by the authors justifies that Newton to be the last name. Note the term momentum was not used until the 16th century. The student can research this on their own and decide if their opinion differs.
2Here we are describing it in terms of force and momentum but you could also look at this concept (as you can most mechanically situations) in terms of energy using work (\(F_{\Delta t} d\)) and kinetic energy (\( {1 \over 2} m v^2\)).
3There is the concept of impact force with units of force which is another way of looking at the impulse force (with units of momentum). The physics of karate usually refers impact force rather than impulse.
4In general it is always easier to use calculus. You will see this as you move further into your courses.

