14.11.3.1: Hydrostatics
- Page ID
- 46444
Hydrostatics is applicable to fluid systems that are not in motion. One of the most common ideas in hydrostatics is buoyancy. This is where an object either floats, or is suspended, or sinks in a fluid. Buoyancy, generally, depends on the fluid being incompressible (liquid).
The force of buoyancy is the main idea for this subject which is dependent on the densities of the fluid the object is partially submerged in and the fluid the object is protruding into. The force equation we would be interested in is1 \(F = mg = \rho V g = g \rho V\) in the context of displacement. Let us say we have an object of volume, V, that is "floating" in a fluid with density \(\rho_1\) in an "atmosphere" of \(\rho_2\). We would first split the object into two parts with volume \(V_2\) representing the volume of the submerged portion of the object and \(V_1\) being the volume of the object in the "atmosphere." Then from there we can assert the force of buoyancy as \(F_b = g \rho_1 V_1 + g \rho_2 V_2\), however we will assume that the "atmosphere" is a gas giving us the final form for the force of buoyancy as
\[F_b = g \rho_2 V_2\]
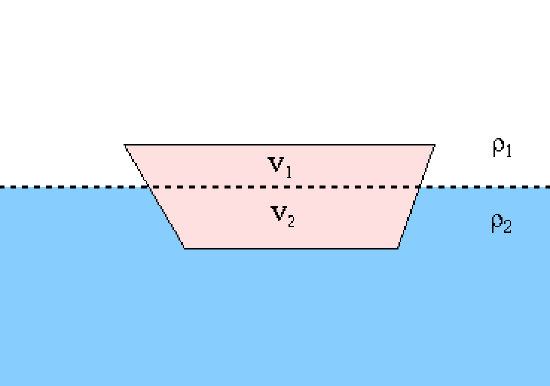 |
| This is a cartoon of an object (a boat, say) floating in a fluid of density \(\rho_2\) and in a fluid of gas of density \(\rho_1\). The force of buoyancy would be based off the displaced weights of each fluid. The displaced weight idea forms the basis of Archimedes' principle. |
If we assume the density of our object is \(\rho_o\) we can determine from this idea if our object will float (\(\rho_2 > \rho_o\)), sink (\(\rho_o > \rho_2\)), or be suspending in the liquid (\(\rho_2 = \rho_o\)). You can also use these ideas to measure the density of objects.
There are many other concepts in hydrostatics but for this introduction we will leave it here and move onto hydrodynamics.
1Technically we should start with a stress tensor known as a Cauchy stress tensor for the force expressed as \(\vec{F} = -\vec{\nabla} \cdot \overleftrightarrow{\sigma}\) (this form of force is typically used in simulations were we use \(\vec{F} = - \vec{\nabla} V\) where V is the potential that is defined by the application). Note that the divergence of a tensor is a vector (like the gradient of a vector), unlike the divergence of a vector which is a scalar.

