14.11.3.2: Hydrodynamics

Hydrodynamics is applicable to systems that are in motion due to or part of a liquid medium. The more important concepts are conservation of mass law and the conservation of energy law which gives you the continuity equation and Bernoulli's equation, respectively.

Continuity Equation

Conservation of mass leads to the continuity equation which we express¹ as

\[A_1 v_1 \rho_1 = A_2 v_2 \rho_2\]

where A is the cross sectional area (with a direction normal to the A). In situations with where the density is constant we can see this equation in action with say a hose (where we restrict the area to increase the velocity).

\[A_1 v_1 = A_2 v_2\]

Cartoon to visually show the flow of liquid as the Area is restricted the fluid's velocity increases.

The equation that is most associated with hydrodynamics is Bernoulli's equation. This principal is really an application of the conservation of energy².

\[{P_1} {V_1} + m_1gz_1 + \frac{m_1 v_1^2} {2} = {P_2}{V_2} + m_2gz_2 + \frac{m_2 v_2^2} {2}\]

Where \(PV\) is a work energy, \(\frac{m v^2}{2}\) is kinetic energy, and \(m g z\) is potential energy.

If you assume density is equal in a steady flow you can rewrite the above equation into its more traditional form. This equation assumes that the fluid is non-viscous, irrotation, and completely incompressible. In addition it assumes no friction loss. Bernoulli's equation is used to design flow meters and is used to partially explain airplane flight though other factors including turbulent flow is an important aspect that it does not handle. Bernoulli's equation is a good approximation for most hydrodynamic flow, but other equations and concepts must for more accurate calculations. In engineering the Bernoulli's equation is usually supplemented (or replaced) with a Moody Chart/Diagram to handle concepts the Bernoulli's equation is not equipped to handle. Another method would be to use the Navier-Stokes equation (which can be intractable in certain instances and requires approximation methods - Numerical Methods!).

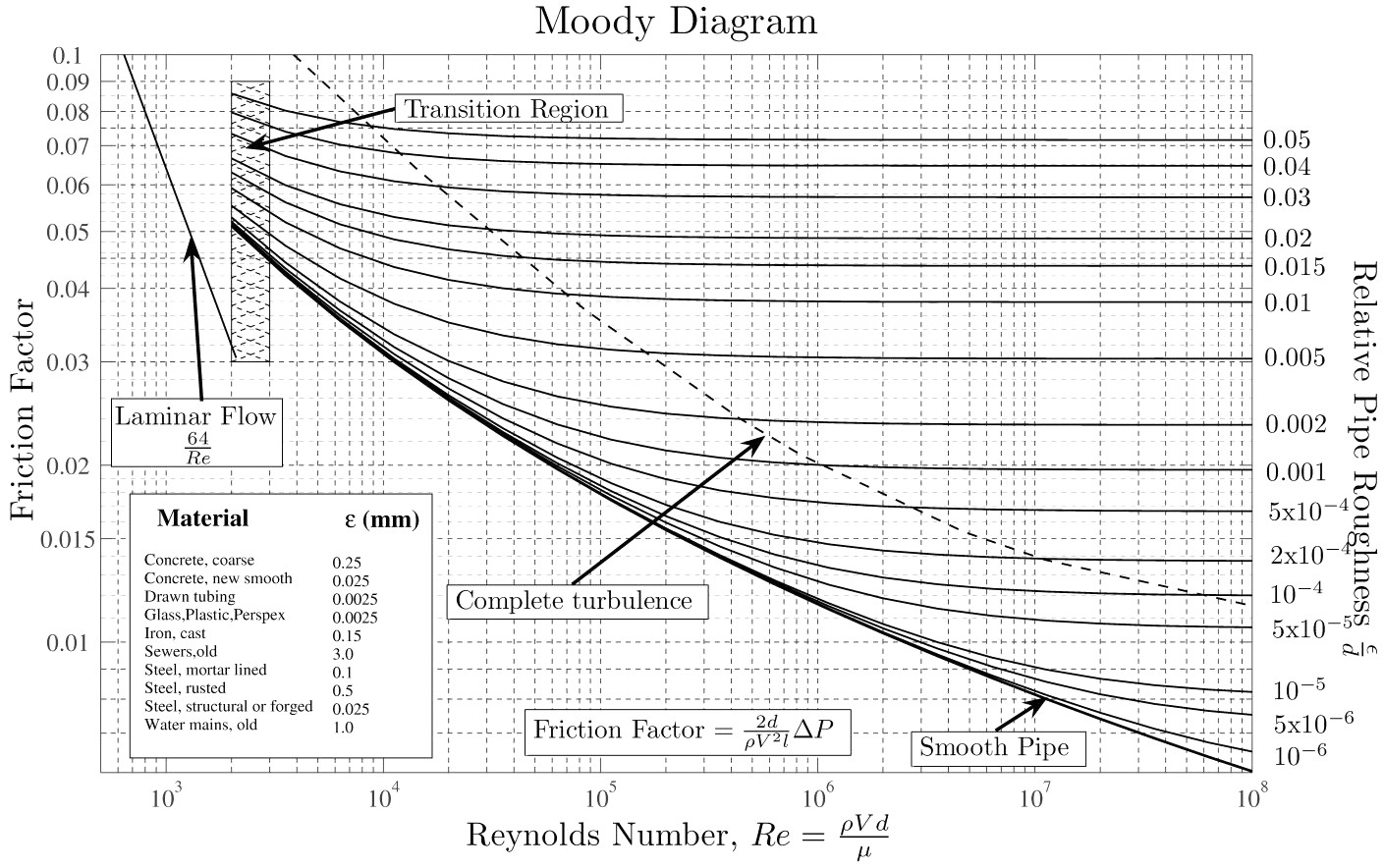A Moody diagram is empirical and takes into account a number of concepts that the Bernoulli's equation does not consider. This image is from Wikipedia from Donebythesecondlaw (CC BY-SA 3.0)

Momentum and fluids

In general it is important to understand momentum and force for fluid motion. Following the dynamics principles described previously we have \(\sum \vec{F} = \frac{d\vec{p}}{dt}\), but unlike previously we can not assume the mass is constant. So following some basics rules of calculus we can rewrite this as \(\sum \vec{F} = \frac{dm}{dt}\vec{v} + m \frac{d\vec{v}}{dt}\) or using Newton's notation as \(\sum \vec{F} = \dot{m}v + m \dot{v}\). The force can be from pressure-volume forces, gravity forces, convection forces, various frictional forces, etc. However if we include these forces found in fluids we need to modify our original equation to include other courses of momentum. A general momentum equation can be formed for a pipe that has the same volume of fluid (so \(\dot{v} = 0\)) flowing through it:

\[\sum \vec{F} = \dot{m}\left(v_{out} - v_{in}\right)\]

A similar equation can be written for a general angular momentum equation.

The continuity equation is derived from the idea of the time varying mass (and moment of inertia) and basically states that the mass (and moment of inertia) must be conserved over time and space.

The idea presented here can be taken into energy-work space with regards to changing energy. You will note that if energy³ has a dynamics component that changes over time you could image your kinetic energy varying as \(\frac{d(\frac{1}{2}mv^2)}{dt}\) which would would expand out to \(\frac{1}{2}\left(\dot{m}v^2 + 2 v \dot{v}\right)\) and your potential energy varying as \(\frac{d(mgh)}{dt}\) which would become (assuming gravity and height are not varying with time) \(gh\dot{m}\). Again we would have a time varying mass (and moment of inertia) which will lead us to a energy-work type equation similar to the general momentum equation. These concepts will be completed in your junior or senior year when you have had your full complement of calculus and differential equations.

Let us look at the Navier-Stokes equation which is based off a general momentum equation.

Navier-Stokes Equations

Navier-Stokes equations⁴ consists of a continuity, momentum, and energy equation for viscous fluids that takes into account. By the very nature of the equation frictional forces are included along with other aspects missed by the Bernoulli's equation. The actual equations are dynamic differential equations. The main equation is a force equals mass times acceleration expressed as \(-V \vec{\nabla} P + mg + \mu V \nabla^2 \vec{v} = m(\frac{\partial{\vec{v}}}{\partial{t}} + (\vec{v} \cdot \vec{\nabla}) \vec{v})\) where the left side of the equation includes pressure-volume force, gravity force, and a Stoke's flow like force (where \(\mu\) is the dynamic viscosity) and the right side of the equation is mass times acceleration⁵ plus a term that represents internal stress forces which takes into account friction/viscosity⁶. Generally this equation is written in terms of density:

\[-\vec{\nabla} P + \rho g + \mu \nabla^2 \vec{v} = \rho \left(\frac{\partial{\vec{v}}}{\partial{t}} + (\vec{v} \cdot \vec{\nabla}) \vec{v}\right)\]

The continuity and energy equation are discussed in the above section enough to give you a general idea and while we have not done a full derivation we hope you can at least get the idea of how these are derived from what you know from general mechanics. A full understanding of calculus and differential equations would be needed to complete this discussion, so for now we will leave it at this.

Darcy's law, vorticity transport, etc. are derivations of and/or extensions of Navier-Stokes equations. There are many "versions" of Navier-Stokes equations usually adding a term from Cauchy's momentum equation. For the most complex situations the Navier-Stokes equations is intractable and numerical methods will need to be used to solve the equations (which is the case for most very complex situations).

Reynolds Number

An important concept in hydrodynamics is the Reynolds number⁷ is defined as the inertial forces to viscous forces. This number defines a clear demarcation between laminar flow and turbulent flow (which is important in aerodynamics). Reynolds number is dimensionless and can be expressed as \(Re = \frac{\rho v l}{\mu}\) where l is the length of the characterization range. Reynolds number below 2000 is laminar flow and greater than 4000⁸ is turbulent flow. Note that between 2000 and 4000 it gets a bit murky between laminar and turbulent flow with a mix of the two to one degree or another. Because of media reports on turbulent flow and the downing of aircrafts there is a general impression that turbulent flow is bad, but this is not the case. Laminar and turbulent flow are neither good or bad but descriptions that maybe bad in certain circumstances and good in others. What is good and bad is more related to the application, not the flow characteristic.

Turbulent flow is a mixed blessing for flight as it is needed for flight, but also dangerous for flight. In general you do not want turbulent flow on the top of a wing which you can get if you take too steep an ascent however other turbulent conditions will help flight. When a nurse or doctor is measuring your blood pressure (auscultation method) what they listen for is the sound of turbulent flow changing to laminar flow (which is silent).

Bernoulli's equation can only be used in a laminar flow region which would mean a Reynolds number less than 2000. For Reynolds number greater than 2000 either a Moody chart or Navier-Stokes equation is more appropriate.

---

¹Technically the principals here should be described by differential equations with the divergence idea we discussed previously, but for this introduction we will stick to the simple expressions. This is true for the continuity equation as well as Bernoulli's equation.

²Conservation of energy is important in electrical circuits as well and leads to the most important equations in that discipline. You will find that all the important equations of engineering (and physics) come from the conservation laws (especially energy, mass, and momentum in an engineering context).

³Note that energy is related to momentum by the equation \(E=\frac{p^2}{2m}\).

⁴The Navier-Stokes equation is a special case of the Cauchy's momentum equation which is a tensor-based differential equation derived from the standard equation of motion \(\vec{F} = \frac{d\vec{p}}{dt}\). As such this includes pressure, stress (the Cauchy stress tensor), and mass flow which is more general then just fluid motion.

⁵Here we use a partial derivative of the velocity with respect to time (because of the energy formalism used here) but if it helps you see this better just use a total derivative of the velocity with respect to time. In the energy formalism, technically Lagrangian formalism, velocity depends on time and position, v(t,x,y,z).

⁶Which is mass times what is called convective acceleration. Convective acceleration is acceleration in a fluid that is convective (see thermodynamics section).

⁷This number would be more appropriately called Stokes number but that name is designated for something else Stokes did so Reynolds number it is...

⁸Others put this number at 3000 or 3500, but since there still maybe a small bit of laminar flow in those regions we will stick with 4000 here, but please do your own research.