14.11.4: Solid Mechanics
- Page ID
- 49049
Solids
This section is on solid mechanics which is just an extension of mechanics to actual materials.1
Continuum mechanics
Solid mechanics is continuum mechanics where objects are not viewed as individual particles but as a whole system from which mechanical properties can be described to. Technically we do that for statics and dynamics as well but in this subject it is viewed more in a "real world" sense, like a solid, not an ideal beam for instance, etc.
Here we will cover only a couple of aspects to give the student an idea of what is taught herein. Many aspects of this subject will not be broached here, just some essential ideas.
Stress and Strain
Stress is an intensity of pulling or pressing defined by the following equation: \(\sigma = \frac{\vec{P}}{A}\) where \(\vec{P}\) is force2 and A is the cross sectional area. There are two types of linear3 stress tensile stress (pulling) and compressive stress (pressing).
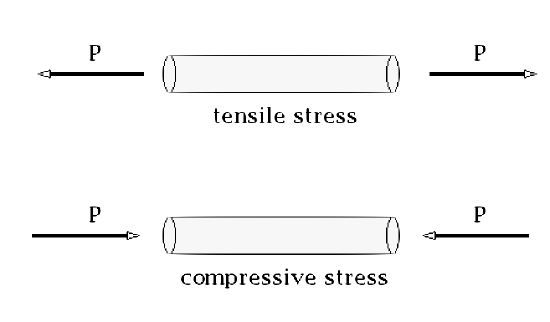 |
| Cartoon of the two types of linear stress where \(\vec{P}\) is a force. |
Strain defines the change in length compared to the original length when stress is applied to a material. The simplest equation for strain is defined as \(\epsilon = \frac{\delta}{L}\) where \(\delta\) is elongation and L is length.
Stress-Strain Curve
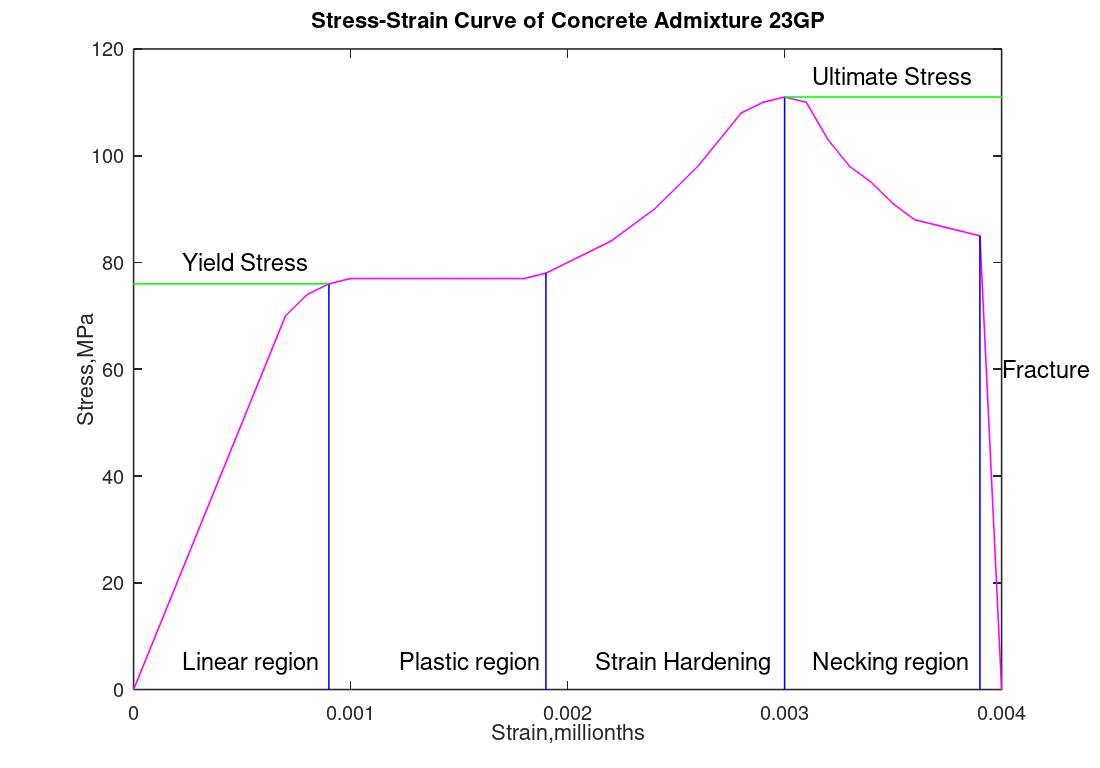
After defining stress and strain we can define one of the most important curves for materials: the stress-strain curve. This curve points out how the material behaves under stress and is useful when considering what materials you would use for a particular application.
 |
|
This is a fictitious stress-strain diagram to show the various regions of a stress-strain diagram might have for different materials. For academic purposes this curve includes all of them which probably would not happen for most materials. Note this curve does not represent ringing in the plastic region which might be seen in some materials. Each region describes a particular way the material behaves. In general you would want the material to perform in the linear region. In order: The linear region is the region where as stress is applied strain rises linearly, this region is the region that is generally useable for structures. Yield stress is the minimum stress where the material will deform without a sizeable load (stress). The plastic region is the region where the material will deform with very little load (stress). That is with a little load the material will change substantially (imagine being on a bridge where that would occur...scary). Strain hardening is a region where there is resistance to strain and is accompanied with a crystalline change (which could be useful in making a new material or not). The ultimate stress is the largest stress the material will tolerate before starting to degrade. The necking region is when the material starts to break in the form of a neck (think of a rubber band that you are pulling hard and it starts to break). Finally the fracture region is when the system will fracture (break). |
Other topics
An outline of some other topics in solid mechanics will help to show what this subject is about. Because a stress really is a tensor this topic cannot be fully fleshed out until junior or senior year of college.
- Tension and compression
- This is an extension of the stress-strain idea
- Hooke's law and Young's modulus would be introduced here
- Thermal stress
- Temperature change can cause stress as well
- Bending stress
- This leads to bending of beams which depend on second moments of area, cross sectional area (your beam might be a hollow cylinder or a solid cylinder for example), and centriod (eg. center of mass or gravity)
- Shear stress and shear strain
- Stress and strain for when one part of the object is stressed but not the other part of the object
- Shear stress and strain due to torsion
- Rotational
- Buckling
- Upright beams, struts, etc.
- Euler's formula which describes critical buckling
- Euler-Bernoulli beam theory (more then just Euler's formula)
- This theory is for beam deflection and load
- Static Euler-Bernoulli equation
- Dynamic Euler-Lagrange equation
- Basically a minimization of energy function
- Solving this is basically an optimization problem (which for intractable problems is a numerical methods problem)
- This theory is for beam deflection and load
- Stress tensor
Nuts and Bolts
Sometimes in solids some useful parts that could be described as technician type parts are looked at as well. Again we will outline this information.
- Screws and bolts
- Axles and shafts considerations
- Bearing stress
- Deflection
- Vibration
- Friction-locked joints types
- Clamped joint
- Where the shaft is clamped shut with a bolt on the end
- Taper joint
- For clamping tapered shafts
- Clamping sleeve
- Circular sleeve commonly used in cryostats, vacuum pumps, etc.
- Friction locked and tightened with hex bolts very similar to a tire on a car
- Clamped joint
Springs
- Springs
- Spring rate is a quantity that describes the amount of deflection of a spring given a certain amount of weight
- Low spring rates are "soft" springs
- High spring rates are "hard" springs
- For springs in parallel between two surfaces the total spring rate is the sum of all the spring rates (like capacitors)
- For springs in series between many surfaces the reciprocal of the total spring rate is the sum of the reciprocal of all the spring rates (like capacitors)
- Types of spring
- Springs that are like diving boards
- Rectangular, trapezoidal, and triangular springs
- Leaf springs
- A number of the springs like diving boards stacked together to form a spring
- Used in wheeled vehicles
- Ring spring
- Combination of many springs
- Springs called either inner and outer springs
- Inner spring compresses while outer spring expands during axial compression
- Kind of like a telescoping spring
- Torsion springs
- Spring that works rotationally rather than linearly
- Types
- Coaxial
- Bar
- Torque rather than force would be a consideration
- Also shear stress is an issue
- Springs that are like diving boards
- Spring rate is a quantity that describes the amount of deflection of a spring given a certain amount of weight
Gears
- Gears
- Involute gear
- Gears with teeth (what you normally think of when you think of gears)
- Gear ratio is the amount of turns on smaller gear (pinion) with one turn of the larger gear (gear)
- This assumes the gears are messed together
- Gear ratio is the number of teeth on the larger gear divided by the number of teeth on the smaller gear \(G = \frac{n_g}{n_p}\)
- Bevel gear
- Cone shape gears that are normally messed at right angles to each other
- Teeth can be straight or spiral
- Epicyclic gearing (planetary gear set)
- A system of involute gears that have an outer ring gear (teeth on the inside of a circular gear) with one or more gears ("planent gears") inside the ring gear meshed with a center gear ("sun gear")
- Large gear ratio in compact space
- Pencil sharpener uses this type of set up
- Used in a number of 3D printers because of the compact space and better control of stepper motors
- Worm gear
- Cylindrical gears with spiral teeth (you will see this gears on a guitar or similar instrument)
- Usually a worm gear is used in combination with an involute gear
- Worm gears are used on guitars (and the like) to tune strings, for conveyor belts, and moving filter wheel in cryostat
- Has very high gear ratios which makes in useful for many other applications
- Involute gear
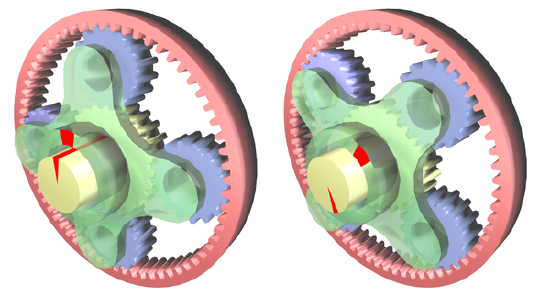 |
 |
| Epicyclic gearing from Wikipedia. Eric Pierce's Own work created in Blender and GIMP. CC BY-SA 3.0 | Worm gears for tuning a mandolin. Note the worm gear is part of the tuners that is connected to an involute gear that moves the shaft with the wound wire on it. |
Bellows
- Bellows
- Leather bellows
- Expandable and compressible
- Basically a leather bag between to pieces of wood that are open and closed to send air into the fire
- Used primarily for stoking fires to make them higher temperature for metallurgy
- Fire pistons are similar systems developed in Asia
- Metal bellows
- Flexible metal structures that expand and compress with vacuum or pressure
- Many uses
- Pressure gauges
- Sealing (especially with toxic gases)
- Coupling for stepper motors
- Compressors
- Vacuum pumps
- Musical pipe organs also have bellows
- Leather bellows
.png?revision=1&size=bestfit&width=438&height=474) |
| Old-fashion bellow that gives you the idea of the modern bellows. There are many web sites on bellows4. This image is public domain from Wikipedia by Pearson Scott Foresman. |
1This course is also know as strengths of materials or for short materials. For schools that have a materials science course this could lead to confusion. In this case schools refer to this course as solid mechanics which is a more general term which can include some of the additional topics that are not really strengths of materials.
2It is customary to use P for the force as it gives the idea of pressure, but it is fine if you want to use F as some do that as well.
3There are other stress like torsional stress (rotation), etc. but that will be reserved for the actual solid mechanics course.
4An instructive web site on the difference between metal bellows and non-meta bellows are at Bellowexpansionjoints.com

