14.13: Electrical Circuits
- Page ID
- 45593
Electrical circuits are very important to all engineering disciplines either because there are electric circuits in those disciplines or because the underlying physical ideas are easily translated to other disciplines. The two most important laws in circuit analysis are the two Kirchhoff's Laws which are just another form of the conservation laws of physics. These laws are ALWAYS valid in every situation. This can get confusing sometimes as some techniques in circuit analysis might seem to violate these rules - they do not, when you encounter these situations remember that they are just shortcuts (approximations).
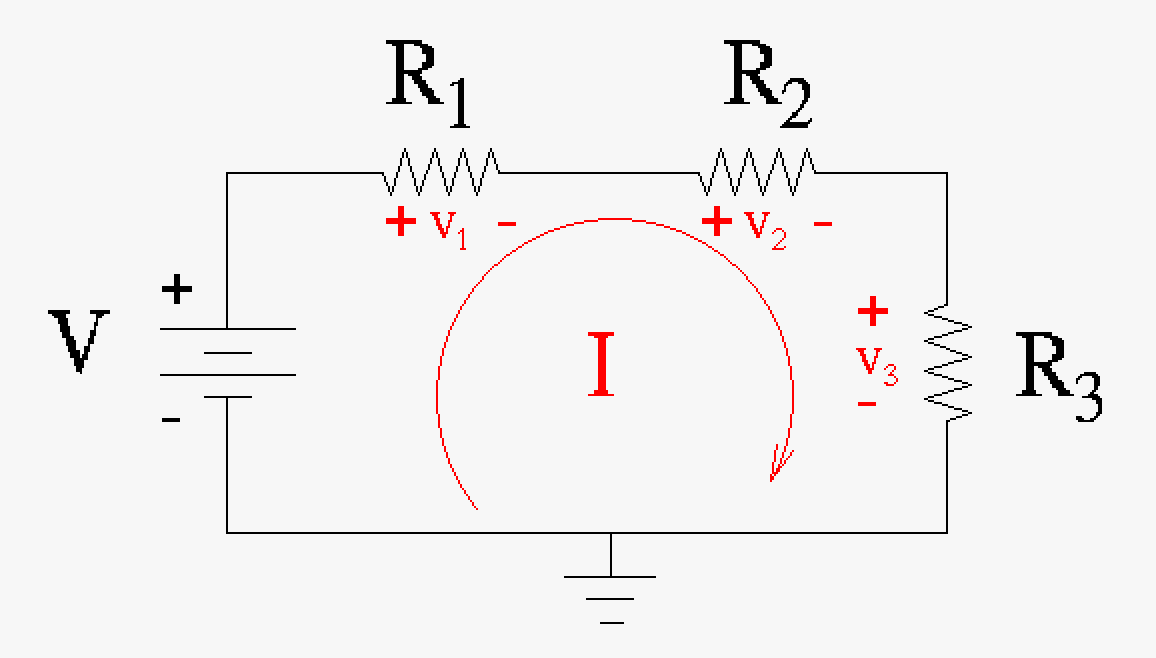
Before we continue we must define some ideas in electric circuits, for instance what is a circuit? A circuit follows from the regular definition of a circuit, a circular path, but with the addition of electrical elements. This is extended to have possible branches off from the original circuit. For each branch of a circuit typically we assign a node as can be seen in the figure below (note: nodes could be defined anywhere though generally you want it to be useful).
 |
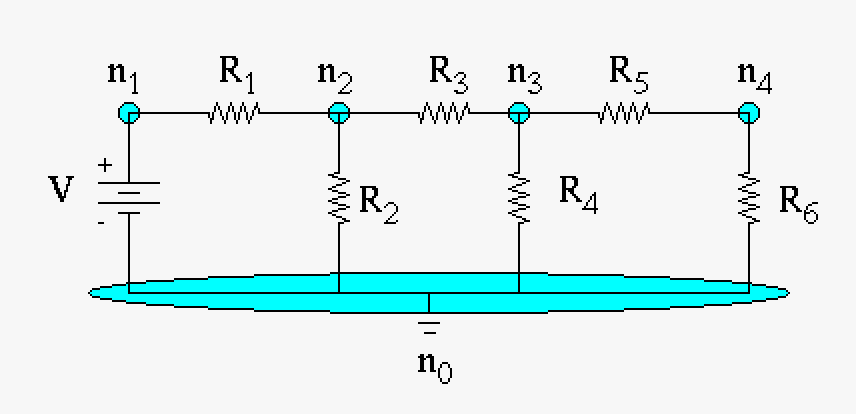 |
| A simple electric circuit consisting of a voltage source and some resisters (example: incandescent light bulbs). If we follow the current loop this would be how mesh analysis is done. For this simple mesh using Kirchhoff's law (presented below) we would get the equation: \(V = v_1 + v_2 + v_3 = IR_1+IR_2+IR_3\) | A circuit with branches (the wire with R2 is the first branch in this circuit) and nodes (n0, n1, n2, n3, and n4). This circuit is a little more advanced and would typically be studied in circuit analysis. Note that there are two types of analysis: mesh analysis which revolves around current loops and node analysis which revolves around the aforementioned nodes. Typically circuit analysis programs (SPICE) use the node analysis method. |
So what are electrical elements? The are the various building blocks of an electrical circuit that represents energy storage and release (as is the case for mechanics as well...see control systems). They are literally hundreds of electrical elements, so here we will just introduce the most important ones to give you a taste of circuits.
Electrical Elements
Passive electrical elements
Passive elements just store and release energy that is originally introduced into the circuit from an active element. The three most important passive elements are the resistor (releases energy into the air by heat), the capacitor (stores energy electrically), and the inductor (stores energy magnetically).
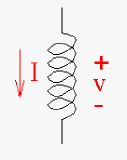
| Element | Resistor | Inductor | Capacitor (Condenser) |
| Constant (Symbol) | R | L | C |
| Electronic Symbol (Schematic) | 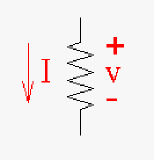 |
 |
 |
| Equation |
v=Ri Ohm's Law |
\(v = L\frac{di}{dt}\) \(i = \frac{1}{L}\int{v(t)dt}\) |
\(i=C\frac{dv}{dt}\) \(v = \frac{1}{C}\int{i(t)dt}\) |
| Physics | Releases energy through heat | Stores energy by means of a magnetic field | Stores energy by means of an electric field |
| Units | Ohms | Henry | Farad |
These elements are often used in control system equivalent circuits.
Active electrical elements
Active elements store and release energy in an active manner with either the redirection of energy or the introduction of energy through an external source (example: an electric plug) or a chemical process (example: a battery). The five most important active elements are the voltage source (example: a battery), current source, transistor (bipolar or FET), diode, and operational amplifier.
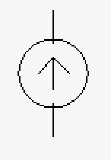
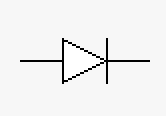
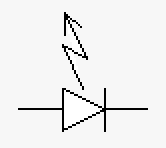
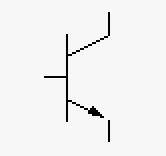
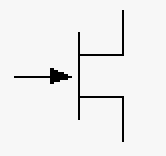
| Element | Voltage source (DC) | Voltage source (AC) | Current source | Diode | Light emitting diode (LED) | Bipolar Transistor | Field Effect Transistor (FET) |
Operational Amplifier (OP amp) |
| Electronic Symbol | 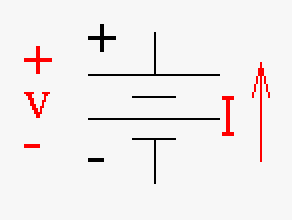 |
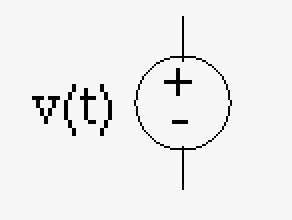 |
 |
 |
 |
 |
 |
 |
| Description | Direct current voltage source | Alternating current voltage source (time varying) | Typically used when you need a constant current | Typically used for rectification of signals | Can be used to detect light or emit light | Generally used for increasing signal levels | Generally used as a switch (0 or 1) in computers typically in on/off pairs |
Multiple uses; see below |
This is definitely not a complete list of active elements but this is good for a quick introduction especially for engineers that might not be going into electrical engineering.
Kirchhoff's Laws
Kirchhoff's Voltage Law
The sum of the voltages in a closed circuit is equal to zero. \(\sum{V_i} = 0\)
Example: Using the simple circuit above we would have \(V - v_1 - v_2 - v_3 = 0\)
Kirchhoff's Current Law
The sum of the currents going into a node are equal to the sum of the currents going out of a node. \(\sum{I_{in}} = \sum{I_{out}}\)
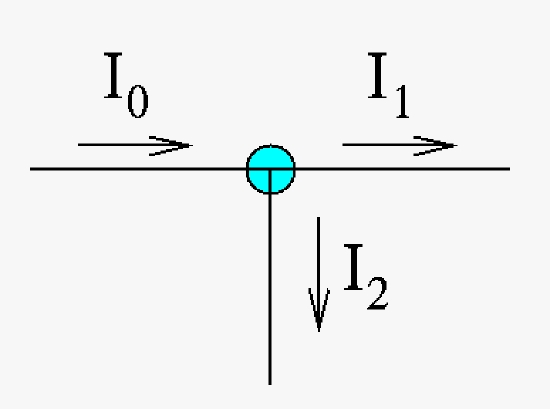 |
| "Current in" is equal to "current out" (or sum of current equals zero if you are consistent in signs). Here we have current I0 entering a node and splitting into current I1 and I2 whose sum is equal to current I0. |
It should be noted that this is a simplification of the actual Kirchhoff's laws which are more complicated and involve partial differential equations (see Kirchhoff's original papers on the subject). These laws however are sufficient for the practitioner to solve circuit problems.
Equivalence Theorem
The equivalence theorem allows the electrical engineer to make an equivalent circuit for a circuit that is for all intensive purposes a black box (example: the plug in the wall - we don't need to know the full circuit; we can just make an equivalent circuit). Measurements can be made on any black box circuit to form an equivalence without knowing the details.
Thévenin's Theorem
Any linear network can be converted to an equivalent form that consists of a voltage source in series with a resistor (or an impedance so as to include other elements).
Norton's Theorem
Any linear network can be converted to an equivalent form that consists of a current source in parallel with a resistor (or an impedance so as to include other elements).
For circuits with a non-linear component the system can be divided into a non-linear portion and a linear portion where the equivalence theorems are still valid.
Non-linear circuits
Diodes, transistors, etc are non-linear and need to be expressed in terms of an I-V characteristic curve. In general the idea of creating a curve to describe elements is used in multiple disciplines of engineering (example: phase diagrams for materials; expansion curves used by civil engineers; etc.). There is a science to using these curves which will be taught in later classes; have fun!
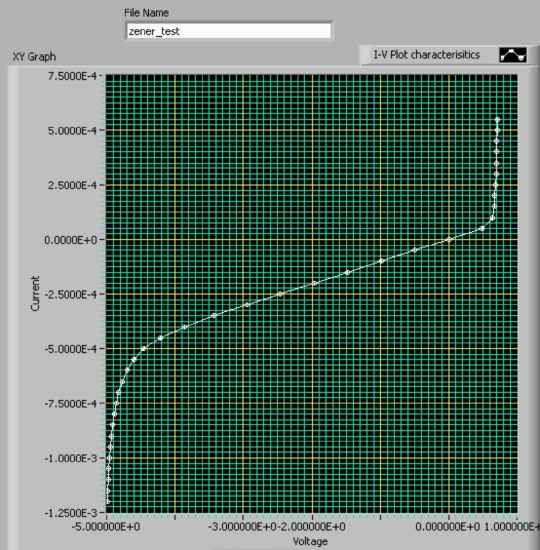 |
| I-V characteristic plot of a Zener diode. This image is an actual result displayed using LabVIEW which is a very useful electrical engineering software package. |
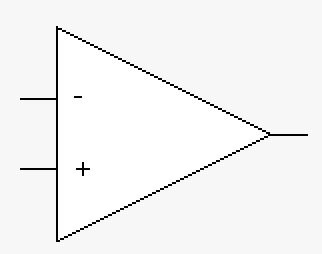
Operational Amplifiers
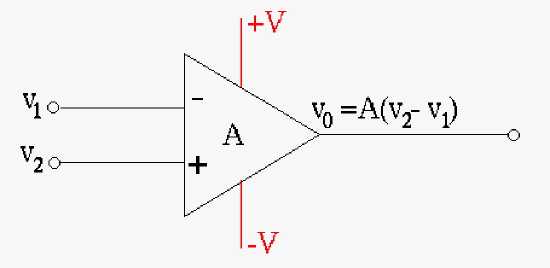 |
| The operational amplifier's function is shown above. The output is difference of the two voltage inputs (\(v_2\) and \(v_1\)) amplified by a gain A. The +V and -V is the power supplied to the amplifier which also limits the output voltage. The output voltage cannot exceed V the supply voltage. |
As a last topic we will review operational amplifiers (opamp) uses but not the details (that is for later classes). An opamp is a device that takes the difference of two inputs and amplifies that signal. This seems to make the opamp a one purpose device, but that would not be accurate. An opamp can be used as a summing amplifier, an inverting and non-inverting amplifier, a voltage follower (used as a buffer), a differential amplifier (used extensively), an ECG amplifier (in the past referred to as an EKG amplifier), instrumental amplifier (extension of an ECG amplifier), level shifter (for sensor calibration), lock-in amplifier, active filters (faster and much better slope then passive filters), differentiator (which takes an analog differential, just like in math), and integrator (which takes an analog integral, just like in math).
An ECG amplifier is the basis of an electrocardiogram though they can be used in a multitude of instruments (though in general an instrumental amplifier would be better). Given the importance of electrocardiogram it is clear how important opamps are to world.
Filters are useful for clearing up poor signals among other uses. Active filters are really much better filters but because they have limitations with voltage, current, and frequencies they do not totally replace passive filters. Passive filters are made with the passive elements (resistor, capacitor, and/or inductor) and while inferior to active filters they still have there uses in high voltage and high current applications.
A differentiator and integrator can be used in an analog computer or a PID controller. While you might think a differentiator and integrator is just doing calculus and question why you would need that, it turns out that differentiation and integration has useful engineering properties that can be used to achieve certain results. While the opamp method is an electrical engineering method there are mechanical ways to differentiate and integrate as well.
For more details enroll in an electric circuit analysis course.
Xfig was used for the images in this chapter. It is a free software which is very useful for various CAD purposes.

