2. Illuminated Characteristics
- Page ID
- 5971
The illuminated characteristics of a diode are similar to the dark characteristics, except that now a light-induced current ("photocurrent") is flowing in the device. This section looks at the effect of incident light on a diode.
Ideal diode under illumination
When an ideal diode is illuminated, the incident light knocks electrons out of their bonds and creates electron-hole pairs. Due to the internal electrical field in the diode, caused by the space charge region, the electrons and holes are forced in opposite directions; this creates a coherent current, called a "photocurrent", because it is driven by light. Because electrons are forced towards the n-type material, and holes forced towards the p-type material, the resulting photocurrent iP runs from n-type to p-type.

Once an incident photon creates an electron-hole pair, the built-in electrical field pushes them in opposite directions. The hole, being positively charged, feels an electrostatic force Fp to the left; the negatively-charged electron feels an electrostatic force Fn to the right.
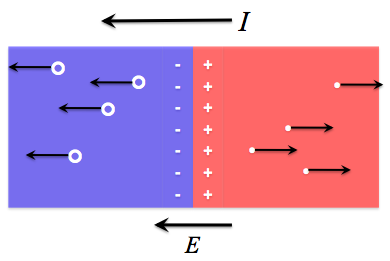
As many electron-hole pairs are created, a substantial current is created. The photocurrent flows
in the direction of the electic field vector: from n-type to p-type.
If the diode is then attached to a load of resistance R, a voltage of v = iPR will develop across the diode.
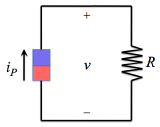
When the photocurrent is wired to a load resistance R, a voltage v = iPR develops across the load -- and across the diode.
Recall that a voltage drop from p-type to n-type is a forward bias. Therefore, the presence of the photocurrent iP induces a voltage that forward biases the diode. As can be seen from the ideal diode equation, a forward bias causes current to flow "forward" as well -- that is, from p-type to n-type. This means that a second current will flow against the photocurrent. This second current is referred to as the dark current, since it is equivalent to the current that flows through a diode in the dark (when it is biased).
To find the resulting current through an illuminated diode, itot, we assume that the total current is simply a superposition of the two opposing currents. Now changing the convention to define the direction of the photocurrent as the positive direction, we can write:
itot = iP - idark.
Assuming that the dark current is described by the ideal diode equation, we can substitute it for idark:
itot = iP - IS[exp(v / ηVT) - 1].
The photocurrent is a function of the incident light spectrum and the material properties of the diode. The incident spectrum can be defined by the function b(E), the incident photon flux density, which gives the number of incident photons of energy E per area per time. The photovoltaic properties of the material can be summed up by its quantum efficiency, equantum(E), which is the probability that one incident photon of energy E will contribute one electron to the photocurrent. When the product of b(E) and equantum(E) -- which gives the number of electrons contributed to the photocurrent due to photons of energy E, per unit area -- is integrated over all values of E, and multiplied by the diode's area, A, an expression for the total number of electrons in the photocurrent is found. Multiplying this by the elementary charge e gives the total photocurrent:
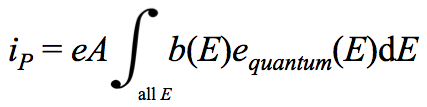
Therefore, the total i-v characteristic of an illuminated diode is given by:

More on quantum efficiency can be found at PVEducation.org, here.
References
"Chapter 6: Diodes." Fundamentals of Electrical Engineering. 2nd ed. New York, New York: Oxford UP, 1996. 363-74. Print.
- Nelson, Jenny. "Chapter 1: Introduction." The Physics of Solar Cells. London: Imperial College, 2003. 9-10. Print.

