3. Equilibrium Carrier Concentration

Last updated
Save as PDF

Page ID: 5955

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Contents

Thermal Equilibrium and the Law of Mass Action
Equilibrium Carrier Concentration with Impurities
References

Thermal Equilibrium and the Law of Mass Action

Another important equation for finding the carrier concentrations in the material is provided by the Law of Mass Action, which before discussing we must first become acquainted with a description of thermal equilibrium. Thermal equilibrium is described by a relationship between the concentrations of charge carriers at a given temperature. In other words, at a set temperature, there is equilibrium between generation (the formation of electron-hole pairs as a result of either thermal excitation or photon absorption) and recombination (the natural destruction of pairs that occurs when electrons from the conduction band fall back into the valence band)².

Let’s discuss the intrinsic case first (undoped semiconductor). In the intrinsic case, the number of bound electrons is much greater than the number of free electrons, therefore the generation of charge carriers is independent of the number of electron-hole pairs that have already been formed. As soon as generation occurs though, recombination comes into play and depends on the concentration of charge carriers in the material. In fact, according to the Law of Mass Action, recombination is directly proportional to the number of charge carriers². This gives

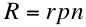
where R is the recombination rate per unit volume per unit time and r is the recombination probability.

Now, in thermal equilibrium the generation rate G is equal to the recombination rate R, and therefore because of the conditions outlined in Intrinsic Carrier Concentration, we have

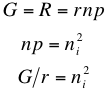
where n_i is the intrinsic carrier concentration. This means that the intrinsic carrier density in a material is determined by the ratio of the generation rate and recombination probability. Therefore the only variable dependence here is on G, which in turn depends on the temperature. It turns out this important relationship holds not only for intrinsic materials, but also for doped semiconductors.

Equilibrium Carrier Concentration with Impurities

Now let’s consider the case with impurities. If we add the intrinsic carrier concentration to the number of free carriers we obtain by doping the semiconductor, we have the equilibrium carrier concentration of the majority carrier in the material. However, it turns out that in most conditions, the doping of the semiconductor is several orders of magnitude greater than the intrinsic carrier concentration. In fact, for Silicon doped with Phosphorous, even at low temperatures (< 70 K) almost all the electrons will be free and located in the conduction band; furthermore, at room temperature, the concentration of conduction electrons in doped Silicon is six orders of magnitude greater than in the intrinsic case, and conductivity increases to the same degree. This means that conductivity becomes dependent on the number of dopant atoms rather than the temperature (doped semiconductors are conductive over a wide temperature range)³.

The above conditions (namely that the concentration of conductive electrons from doping is much greater than that from the intrinsic, and that nearly all the dopant atoms are ionized) imply the number of majority carriers is approximately equal to the doping, as given in the condition below.

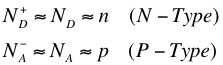
In the equations above, N_D and N_A are the concentration of donated electrons and concentration of accepting holes respectively. Using the Law of Mass Action from the section above, we get the following equations¹:

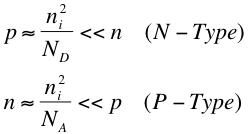
These relations just mean that in an doped semiconductor, we have that the concentration of minority carriers is much smaller than the concentration of majority carriers.

References

1. Green, Martin A. Solar Cells: Operating Principles, Technology, and System Applications. Englewood Cliffs: Prentice-Hall, Inc., 1982. Full book ordering information at www.pv.unsw.edu.au.

2. Goetzberger, Adolf et.al. Crystalline Silicon Solar Cells. Chichester: John Wiley & Sons Ltd., 1998.

3. Honsberg, Christiana, and Stuart Bowden. "Equilibrium Carrier Concentration." PVEducation.org. Web. 24 Jul 2012. <www.pveducation.org/pvcdrom/p...-concentration>.