12.7: Designing for Creep Resistance - Nickel Based Superalloys
- Page ID
- 31528
With over 100,000 flights a day, jet engines are commonplace in today’s world. Jet engines work more efficiently at higher temperatures. Turbine entry temperatures can be of the order of 1,500°C and, while cooling channels and Thermal Barrier Coatings ensure that the blades do not reach these temperatures, they may be at around 1,000°C - a temperature at which most metals are likely to undergo rapid creep under the stresses concerned (~100 MPa). The gradual deformation of these blades is not only financially costly, as they will have to be replaced, but could lead to catastrophic failure and hence, in some cases, loss of life. This is why it’s important to understand the creep behaviour of the materials we use and moreover how we can produce materials with improved creep resistance. Diffusion and dislocation motion are the main mechanisms by which the creep of materials occurs and as such limiting them is key to designing creep resistant materials. Jet engine blades are made from Nickel-based superalloys. A brief outline is presented here of how they are designed, given that resistance to creep at very high temperatures is a key requirement.
Limiting Diffusion
1.Homologous temperature
The (substitutional) diffusivity of a material depends on how easily atoms move between vacant sites in the lattice (see more here), and on the vacancy concentration. Both jump rates and vacancy concentrations are higher at higher temperatures, approaching limiting values close to the melting temperature. It is thus the homologous temperature (T/Tm) that is important. For example, diffusion (and hence creep) rates are relatively high at room temperature for Pb (T/Tm ~0.5), but negligible for Ni (T/Tm <0.2). There are clearly advantages in using materials with high melting temperatures.”
2.Grain structure
There are two important points to be made regarding grains. Firstly, grain boundaries themselves are detrimental to creep resistance because they provide fast diffusion paths through the material and thus accelerate (Coble) creep. Secondly, the length of a grain in the direction of applied stress dictates the distance an atom must diffuse in order to reach the “polar” regions from the “equatorial” regions. Elongating the grains parallel to the applied stress direction will thus tend to reduce the creep rate. The latter effect can be obtained with a columnar grain structure, which is relatively easy to create using controlled directional solidification. Even better is a single crystal (with a selected crystallographic orientation). This requires somewhat greater control during the casting process, although it can be done and this is now routine for many types of blade. The figure below illustrates this.
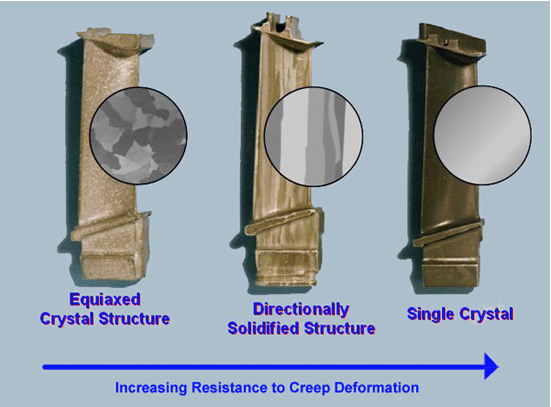
Progression in manufacture of creep-resistant microstructure over time
3.Crystal Structure
In addition to the homologous temperature, there are other factors that can affect the diffusivity. These include the crystal structure, which dictates both the packing density and the nature of the paths taken during atomic jumps between vacant sites. In general, diffusive jumps are more difficult in close-packed, high-symmetry structures, such as fcc. There are also additional factors related to crystal structure. For example, diffusion is difficult in ordered structures, since diffusion tends to create disorder (that is thermodynamically opposed). The microstructure of Ni-based superalloys is typically a 2-phase one, composed of an intimate mixture of γ (fcc Ni) and γ’ (an ordered structure based on Ni with Al and/or Ti), with coherent or semi-coherent interfaces between them. These structures are illustrated below.
Limiting Dislocation Motion
While the two are often inter-related during creep, it is important to inhibit dislocation motion, as well as diffusion. This happens in several ways in Ni-superalloys. One of these concerns the ordered γ’ phase. An ordered structure is degraded, not only by diffusion, but also by dislocation glide. Such motion is therefore opposed, an effect often described as order hardening. (In fact, if dislocations move in pairs, sometimes termed superdislocation pairs, then the second of the pair may restore the order, but this does impose a constraint on the motion - see below.) There is also an effect of the coherency of the γ /γ’ interface, which creates lattice strain in the vicinity. This also tends to inhibit dislocation glide.
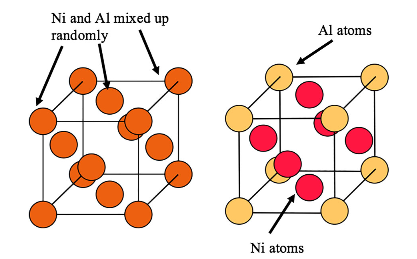
Unit cell of γ on the left and that of γ’ on the right [2]
Precipitates of γ’ exist within a γ matrix, and so dislocations will have to pass from γ to γ’ in order to move through the alloy. The shortest Burgers vector in γ is (a/2)<110>, but in γ’ this is not a lattice vector. As a dislocation passes from γ to γ’ its Burgers vector must be maintained and it will create a region with unfavourable bonding (an anti-phase boundary) and hence an associated energy cost. Its motion is therefore slowed considerably in γ’ compared to that in γ, and it can only travel at any appreciable rate through γ’ once another dislocation passes into γ which restores the unfavourable bonding back to its ordered state – as they move through together the anti-phase boundary maintains a constant width and there is thus no added cost to their motion through γ’. This can be seen in the micrograph below:
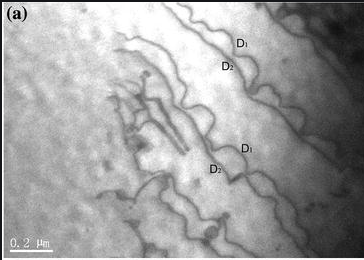
Micrograph showing dislocations passing through a Ni superalloy [3]
It can be seen that dislocations D1 are impeded by γ’ precipitates with D2 following unimpeded. This mechanism results in much slower dislocation glide through the alloy as a whole and so is effective in reducing the rate of dislocation creep. The finer the dispersion of γ’ precipitates the more effective the strengthening will be. The two dislocations that pass through γ’ together are called super-partial dislocations and the sum of their burgers vectors is a lattice vector - a<110> - in the γ’ phase. It is important to note that the γ - γ’ interface is coherent and therefore coarsening does not occur over time.
[2] Y. M. Wang-Koh (2017) Understanding the yield behaviour of L12-ordered alloys, Materials Science and Technology, 33:8, 934-943, DOI: 10.1080/02670836.2016.1215961
[3] Lv, X., Sun, F., Tong, J. et al. J. of Materi Eng and Perform (2015) 24: 143. https://doi.org/10.1007/s11665-014-1307-y


