16.6: Other Porous Structures
- Page ID
- 7890
Many other porous structures show the same type of stress-strain behaviour. The basic reasons are similar. The initial behaviour is elastic, until the stresses in the struts reach their flow or fracture stress. There is then a plateau region as the cells collapse, until the struts from opposite sides of the cells impinge on one another and the applied stress increases more rapidly. However the details can be very different. For instance the struts in ceramic foams tend to break, but a plateau region is still seen.
Many combinations of material and cell structure are possible. Seeing how the cells deform in a foam is more difficult than in the simple honeycomb. However this has been done using X-ray tomography as shown in the short video.
https://www.doitpoms.ac.uk/tlplib/de...s/compress.mp4
Deformation of cells in foam
(For further details see J.A. Elliott et al, “In-situ deformation of an open-cell flexible polyurethane foam characterised by 3D computed microtomography”, J. Mater. Sci. 37 (2002) 1547-1555.)
Looking at the large cell on the right-hand side, it is clear that the deformation of the foam is similar to the honeycomb and the strain comes predominantly from the bending of the struts transverse to the loading axis.
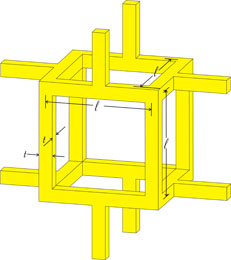
For simplicity, consider the open-cell foam as having a cubic unit cell as shown below.
 |
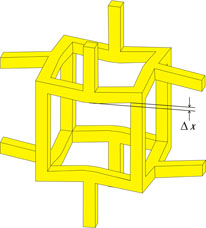 |
Note that each transverse strut has a vertical strut half-way along it, so that axial loading causes the struts transverse to the loading axis to bend, as shown in the diagram above. The Young modulus can now be estimated in a similar way to that for the honeycomb, except that the struts are assumed to have a square cross-section, rather than being rectangular as before and θ, the angle between the transverse strut and the horizontal is 0.
This gives an expression for the relative Young modulus, E/ES, as
\[\frac{E}{E_{\mathrm{S}}}=k\left(\frac{\rho}{\rho_{\mathrm{S}}}\right)^{2}\]
where E is the Young modulus of the porous material and ES that of the solid material and k is a numerical constant, experimentally found to approximately equal to 1 (derivation).
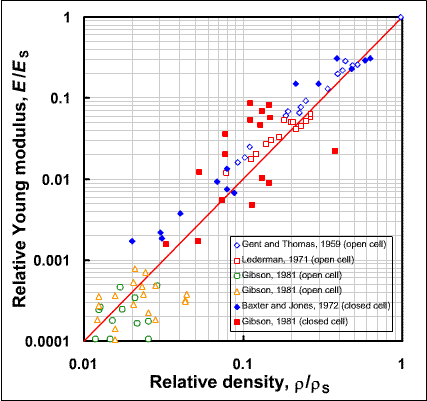
As can be seen in the graph above, experiments show this is correct for isotropic, open-cell foams and even appears to be obeyed where the struts are not slender beams and also, at least approximately, where the cells are closed rather than open. This is thought to arise because in most closed-cell foams most of the material is still along the edges of the cells, rather than being uniformly distributed across the faces. (The data is taken from various sources cited in L.J. Gibson and M.F. Ashby, "On the mechanics of three-dimensional cellular materials", Proc. Roy. Soc. A, 382[1782] (1982) 43-59.)


