23.7: Viscoelasticity and Hysteresis
- Page ID
- 32711
Some biomaterials show a time-dependent elastic behaviour. Although, in the elastic regime, the strain is recoverable, the stress-strain curve is not the same for loading and unloading. Such materials instead exhibit viscoelasticity, involving both elastic and viscous components, which at normal loading and unloading rates leads to hysteresis. A typical hysteresis curve is shown below, and the energy absorbed during one loading-unloading cycle is given by the area within the loop. The shape of the loop depends on the rates of loading and unloading (unlike normal time-independent elasticity).

Hair
The effect of hysteresis can clearly be seen in hair. Hair consists of keratin, which is a type of protein. There are two main forms of keratin: α-helices, which are found in hair, and β-sheets. As the names suggest, α-helical keratin (also known as α-keratin) contains keratin molecules arranged in helices and held in place by hydrogen bonds, whereas β-sheet keratin (also known as τ-keratin) contains keratin molecules arranged in flat sheets, in which adjacent molecules are antiparallel due to more favourable interactions between side-groups.
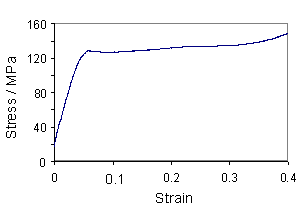
As hair is stretched, the hydrogen bonds between the α-helices rupture, causing the helices to unravel to form β-sheets. The curve for human hair, and a curve obtained for a horse hair from a violin bow are shown below.
|
Stress-strain curve of a human hair (Structural biomaterials, Vincent) |
Measured stress-strain curve of a horse hair from a violin bow |
When the stress on the hair is removed, the helices re-form over time, and since the unravelling of α-helices to form β-sheets is a high-energy-absorbing process, a large area is contained within the hysteresis loop. As a result, this energy is unavailable for fracture, giving a high toughness. This is particularly important for hooves and horns, which are also made up of keratin.
The following graph shows experimentally measured stress-strain curves for human hair, dry horse hair (as used in violin bows) and replasticized horse hair (the same type of horse hair but soaked in water).

As you can see, the replasticized horse hair requires less force to stretch than the dry horse hair (for the same extension). This is because the presence of the water allows the unravelling and reravelling of the helices to occur more easily.
If the human hair had been stretched to a higher strain, its hysteresis curve would look more like this:

Spiders’ silk
There are two main types of silk: spiders’ silk and the silk produced by silk worms. Both types have very good mechanical properties, are durable and readily available, and both form fine threads (typically about 1 μm in diameter) that are biodegradable and biocompatible, making them ideal for use as suture materials.
The two silks are proteins and are very similar in composition: they are made up of similar proportions of the same amino acids. However, the sequence of these amino acids in spiders' silk is much less regular than that from silk worms, impeding the formation of crystallites (micelles) and making it much more extensible.
Spiders produce silk in several different glands, each of which produces silk for a different purpose (wrapping prey, producing drag lines, forming frame threads and capture threads etc). Slightly above the concentration of protein found in the gland, the silk proteins form a liquid crystalline phase. This liquid crystalline phase is formed as the silk passes through the duct leading to the spinnaret, and the silk crystallizes as it passes through the spinnaret itself to form an insoluble β-sheet. The higher the draw ratio through the spinnaret, the higher the orientation of the fibres.
Frame threads contain well-aligned molecules, and are highly crystalline, dry and relatively thick. In contrast, capture threads contain less-aligned molecules, and are less crystalline, plasticised, relatively thin, and exist as coiled fibres within an 'aqueous glue' layer.
The coefficient of restitution, or resilience, describes the fraction of energy returned elastically and can vary by a very large amount, as seen in the table below.
| Resilin | Found in the wing hinges of insects | 97% |
| Collagen | Found in tendons, ligaments, skin etc. | 93% |
| Elastin | The main elastic protein of vertebrates | 76% |
| Viscid silk | Capture threads | 35% |
Capture threads are made from a material known as viscid silk and are used to capture prey. Viscid silk has a very low coefficient of restitution, making it ideal for absorbing the energy of an insect flying into the web (instead of catapulting it away!). Its high strength also helps to ensure that the web is not destroyed upon impact. The hysteresis curve for viscid silk is shown below.

Silk from silkworms

silkworm starting spinning a cocoon © Michaal Cook www.wormspit.com
Silk is used in nature by silk worms to form their cocoons, and so must be strong and not easily breakable, as this would kill the silkworm, preventing it maturing into a moth and reproducing. Silkworms originate from China, India and Japan, and have been used by humans to make silk since at least 3,000 BC. Although silkworms only live for two months, they manage in this time to eat roughly 30,000 times their initial weight. It is estimated that 2,500 to 3,000 cocoons are needed to make just one yard of silk fabric, so despite silk being an excellent material for making fibres it is also expensive to produce.