1.12: Questions

Quick questions

You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!

Which of the following half-reactions represent a general corrosion process?

a	M + 2e → M^2+ and H2 → 2H^+ + 2e
b	M → M^2+ + 2e and H2 → 2H^+ + 2e
c	M^2+ + 2e → M and H2 → 2H^+ + 2e
d	M → M^2+ + 2e and 2H^+ + 2e → H2

Answer

A. Incorrect. The metal dissolution reaction does not conserve charge � the electrons should be on the right hand side

B. Incorrect. These half-reactions both show oxidation. There is no reduction process and so there cannot be a balanced reaction

C. Incorrect. Now the metal is being deposited from its ions. The oxidation reaction is also unlikely to happen as there is not going to be enough dissolved hydrogen to consume electrons at a significant rate.

D. Correct.

Which of the following are possible cathodic reactions that accompany corrosion

a	2H^+ + 2e → H2
b	O2 + 4H^+ + 4e → 2H2O
c	4OH^- → O2 + 2H2O + 4e
d	Mn^z+ + ze → M

Answer

A, C, D

Which of the following is not a form of Tafel's equation?

a
b
c
d

Answer

A.

This is not a form of the Tafel equation. There is a similar form of the Tafel equation:

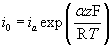
Using the electrochemical series, which of the following metals can be used as a sacrificial anode for steel under standard conditions? Click on this link to launch the electrochemical series in a new window.

a	Nickel
b	Zinc
c	Magnesium
d	Tin

Answer

A. Incorrect Ni and tin have standard electrode potentials more positive than iron in the electrochemical series, so iron sits to the left of them on the Tafel plot. The anodic branch of the iron Tafel plot intersects the cathodic branch of the nickel or tin plot, so iron corrodes and nickel acts as a site of reduction (i.e. as the cathode)

B. Correct. Zinc and magnesium have standard electrode potentials more negative than iron (the main constituent of steel) in the electrochemical series and there is a bigger driving force for corrosion of zinc and magnesium than iron (given by the expression ΔG = − z F Δ E). On the Tafel plot, this would result in the zinc and magnesium plots being centred at lower potentials than the iron plot. The anodic branch of the zinc or magnesium would then intersect the cathodic arm of the iron plot, meaning that the zinc or magnesium corrodes and the iron acts as a cathode

C. Correct. Zinc and magnesium have standard electrode potentials more negative than iron (the main constituent of steel) in the electrochemical series and there is a bigger driving force for corrosion of zinc and magnesium than iron (given by the expression ΔG = − z F Δ E). On the Tafel plot, this would result in the zinc and magnesium plots being centred at lower potentials than the iron plot. The anodic branch of the zinc or magnesium would then intersect the cathodic arm of the iron plot, meaning that the zinc or magnesium corrodes and the iron acts as a cathode

D. Incorrect. Ni and tin have standard electrode potentials more positive than iron in the electrochemical series, so iron sits to the left of them on the Tafel plot. The anodic branch of the iron Tafel plot intersects the cathodic branch of the nickel or tin plot, so iron corrodes and tin acts as a site of reduction (i.e. as the cathode)

Look at the following Tafel plot. What is the critical current density?

a	15 μA m^-2
b	1.5 A m^-2
c	32 A m^-2
d	0.3 μA m^-2

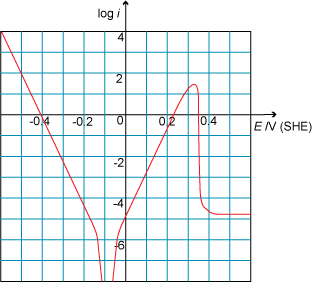
Answer

A. Incorrect. This is the passive current density.

B. Incorrect. This would be the critical current density if the Tafel plot were plotted with a linear y-axis. The y-axis is the log of the current density, hence the critical current density is 10^1.5 or about 32.

C. Correct

D. Incorrect. This is the exchange current density.

Deeper questions

The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.

Draw the Tafel plot of the following information on graph paper and find:

a) The corrosion potential
b) The corrosion current density
c) How long would a 3 mm thick component survive in this scenario (use Faraday's law)
Both reactions have b_a = -b_c = 0.12 V / decade.
One half-reaction has an equilibrium potential -0.25 V (SHE) and an exchange current density of 10 μA m^-2. This reaction has a passivation potential 0.15 V (SHE) and passive current density 10 mA m^-2.
The other half-reaction has equilibrium potential 0.8 V (SHE) and exchange current density 0.1 mA m^-2.
The metal corroding forms 2+ ions, has a molar mass of 35 g mol^-1 and has a density of 6400 kg m^-3.

Answer

a) The corrosion potential is the potential at which the anodic branch of the Tafel plot centred on the lower equilibrium potential (the one lower down the electrochemical series) meets the cathodic branch of the higher Tafel plot
b) The corrosion current density is the current density at the intersection of the two Tafel plots. Remember that the vertical axis is a logarithmic scale.
c) The corrosion current density, i, is 0.1A m^-2. This means that the number of moles of electrons being released by the metal is: 0.1/F (Faraday’s constant, 96485 C mol^-1).

The metal corrodes according to the formula M → M²⁺ + 2e and so releases two electrons for every metal atom that corrodes. The number of metal atoms corroding is always half the number of electron released. Therefore, the number of metal atoms corroding is:

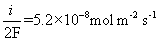
The mass lost per unit area per unit time is the number of moles of atoms lost multiplied by the molar mass, A_r of the metal:

Therefore the thickness, x lost per second is the mass lost per unit area per unit time divided by the density (mass per unit volume).

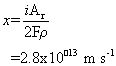
From this, the lifetime of the component, T, can be calculated by dividing the thickness, t, of the component by the corrosion rate (the quantity just calculated):

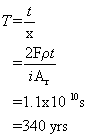
a) Write balanced half-reactions and the overall reaction for an iron water pipe corroding in fully aerated water under standard conditions, and with the water flowing at such a rate to maintain a diffusion layer 1 μm thick.
b) Derive the anodic and cathodic Tafel slopes for the two halves of the reaction if α = 0.5
Using the fact that the iron does not passivate in the potential range being considered, some of the data in this window and the other information and answers above, draw the Tafel plot on graph paper, and then calculate
c) The corrosion potential
d) The corrosion current density
e) Whether or not the pipe will survive 1 year if it has walls 5 mm thick
f) What happens if the pipe is part of a sealed system such as central heating?
g) Why else might your answer to c) be flawed?

Answer

a) The half-reactions can be found in the electrochemical series [link to electrochemical_series.pdf], though remember all reactions are written as reduction reactions for the purposes of the electrochemical series. The one occurring at the lower equilibrium potential will be forced to run backwards and form the anode. Here, this is the iron metal corroding to Fe²⁺ ions. To get the overall reaction, the same number of electrons must appear on both sides of the reaction (charge must be conserved). First, either the iron corrosion reaction is doubled to read:
2Fe²⁺ + 4e → 2Fe
or the oxygen reduction reaction is halved to give
½O₂ + 2H⁺ + 2e → H₂O.
The two reactions are then simply added like you would with simultaneous equations to give:
½O₂ + Fe + 2H⁺ + 2e → Fe²⁺ + H₂O + 2e
or, if the iron corrosion reaction was doubled,
O₂ + 2Fe + 4H⁺ + 4e → 2Fe²⁺ + 2H₂O + 4e
Either way, the same number of electrons appears on both sides of the equation and so the electrons can be cancelled to give the overall reaction. Sometimes, other species appear on both sides of the reaction. These may be cancelled, like the electrons, as if they were variables in an equation.
Remember the formula for anodic Tafel slope, b_a

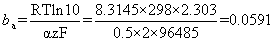
and for the cathodic Tafel slope, the number of electrons must be consistent with that in the anodic Tafel slope, otherwise the two plots will not represent two halves of the same reaction. In other words, both reactions must be expressed in the same number of moles of any given reagent (e.g. both per mole of iron, or both per mole of oxygen, etc.)

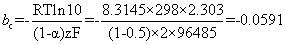
c) The corrosion potential is the potential where the anodic branch of the iron Tafel plot meets the cathodic branch of the oxygen evolution plot. This occurs at –0.08V (SHE).
d) The corrosion current density is the current density when the anodic branch of the iron plot crosses the cathodic branch of the oxygen reduction plot. This occurs at 46.3 A m^-2. Remember that the y-axis is a logarithmic scale.
e) Using the corrosion current of 46.3 A m^-2, the number of moles of electrons being released/consumed can be calculated using Faraday’s constant:

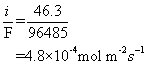
Iron corrodes to form 2+ ions. The rate of iron consumption is therefore half that of the rate of consumption of electrons.

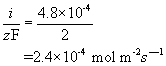
This can be converted to a rate of mass loss per unit area by multiplying by the molar mass


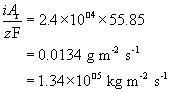
Dividing by the density of iron gives the volume lost per unit area per unit time, or, more simply, the thickness lost per unit time:

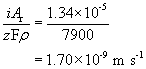
Dividing this by the total thickness gives the lifespan of the pipe:

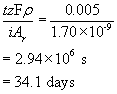
f) As oxygen is consumed in the cathodic reaction, the oxygen concentration in the bulk falls. This in turn slows the supply of oxygen to the cathode and limits the rate at which electrons may be used up. Electrons must not be created at the anode and then not used up in the cathode - charge must be conserved, so corrosion slows. Eventually, the hydrogen evolution reaction will take over as the dominant cathodic reaction. With the HER, the corrosion potential will be about -0.16 V and the corrosion current density will be about 4.5 A m^-2. If the HER were the cathodic reaction from the start, the pipe would have a lifespan of almost exactly one year. This can be verified by adding a HER plot to the Tafel plot of iron and oxygen and following the same process used previously in the question.