17.6: Passage of Particles Through Filter
- Page ID
- 8281
Mechanical filtering (trapping particles in some sort of mesh or porous medium) is an obvious method of removing harmful particulate from a fluid (notably both air and water), although it is not really a suitable approach to obtaining or classifying powder fractions. (While it is sometimes possible to clean, or "regenerate", filters, it's not normally practicable to extract powder from them.) Key filtration issues relate to the twin (conflicting) requirements of trapping (fine) particulate, while avoiding substantial inhibition of the fluid flow. The latter may concern clogging, and the possibility of periodic removal of trapped material, but a fine filter, even when clean, may require a relatively high pressure drop across it to create the necessary flow rate.
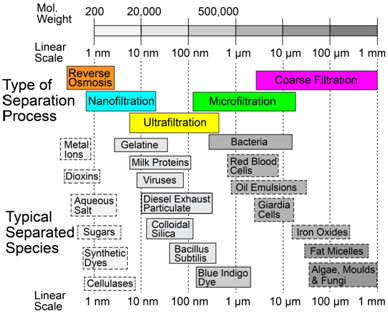
There is interest in filtration of many species from fluids, ranging from coarse inorganic suspensions to small dissolved ions. This is illustrated in the figure below, which shows some of the terms commonly used to denote different types of filtration and corresponding length scales. Small molecules and ions cannot be removed via mechanical entrapment and require precipitation or osmotic separation. However, provided a suitably fine permeable medium is available, mechanical filtration can be effective for very small species (down to ~1 nm), although this may be at the cost of very low fluid flow rates - see below.
The pressure drop (Δp) across a filter of thickness Δx, needed to generate a fluid flux through it of Q (m3 m‑2 s‑1) is dictated by Darcy’s law
\[ Q = \frac{\kappa}{\eta} \frac{\Delta P}{\Delta x} \]
where η (Pa s) is the viscosity of the fluid and κ (m2) is the specific permeability of the medium (filter). Finer filters do, of course, tend to have lower permeabilities, leading to larger pressure drops and/or lower flow rates. This equation can be used to explore specific filtration requirements. There are expressions available for prediction of the permeability of a porous medium, such as the Carman-Kozeny equation, which is described here.
In the simulation below, a flow situation can be set up in terms of applied pressure gradient (pressure drop and filter thickness), filter type (fibre or particle size and porosity level) and fluid type, both chosen from a small number of options. (The DPF option for filter type is a Diesel Particulate Filter - see the following page.) For each of these, the Carman-Kozeny equation is used to give a permeability, which is then employed to predict the fluid flux (represented as the velocity of markers - there is no depiction of particles becoming trapped in this simulation).


