6.3: Strength of Long Fibre Composites
- Page ID
- 8201
For a body under the application of an arbitrary stress state the three most important modes of failure are:
- Axial tensile failure
- Transverse tensile failure
- Shear failure.
 |
 |
 |
|
axial tensile failure
|
transverse tensile failure
|
shear failure
|
Axial Strength
In the simplest scenario, it is assumed that both the matrix and the fibres deform elastically and subsequently undergo brittle fracture. The EQUAL STRAIN condition applies and there are two possible cases:
a) The matrix has the lower failure ( ultimate) strain ( εfu > εmu )
b) The fibre has the lower failure strain ( εfu < εmu )
Click here to see the notations used.
Case a):
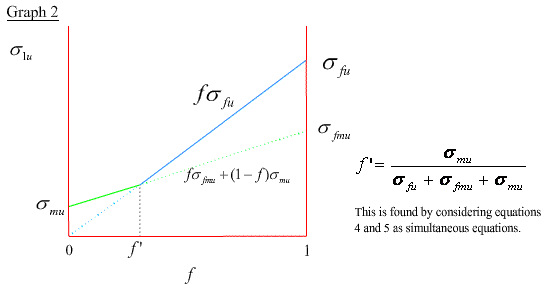
The composite stress is given by the rule of mixtures σ1 = f σ f + (1 - f) σm up until the strain reaches εmu . Beyond this point the matrix undergoes microcracking and the load is progressively transferred to the fibres as cracking continues. During this stage there is little increase in composite stress with increasing strain. With further crack growth, if the entire load is transferred to the fibres before fibre fracture, then the composite stress, σ1, becomes fσf and the composite failure stress, σ1u, is simply f σfu :
σ1u = f σfu (4)
Alternatively, if the fibres fail before the entire load is transferred onto them the composite strength is just the weighted average of the failure stress of the matrix, σmu , and the fibre stress at the onset of matrix cracking, σfmu :
σ1u = f σfmu + ( 1 - f ) σmu (5)
The variation of σ1u with f is shown in graph 2.
Case b):
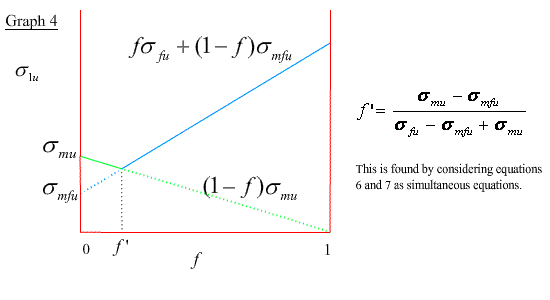
Again, the composite stress is given by the rule of mixtures σ1 = f σf + ( 1- f ) σm up until the strain reaches εfu when the fibres fail. Beyond this point the load is progressively transferred to the matrix as the fibres fracture into shorter lengths. Assuming that the fibres bear no load when their aspect ratios are below the critical aspect ratio, s* = σf* / 2τi* , which is the critical ratio of the fibre length to its diameter below which the fibre cannot undergo any further fracture, then composite failure occurs at an applied stress of ( 1 - f) σmu .
σ1u = ( 1 - f) σmu (6)
Alternatively, if the matrix fracture takes place while the fibres are still bearing some load, i.e. the fibre aspect ratio is more than the critical value, then the composite failure stress is the weighted average of the fibre failure stress, σfu , and the matrix stress at the onset of fibre fracture, σmfu.
σ1u = f σfu + ( 1 - f) σmfu (7)
The variation of σ1u with f is shown in graph 4.
Why is this approach inaccurate?
See Axial strength inaccuracy.
Generally , the fibre volume fractions fall in the range 30% to 70% (ie, > f ') and since it is usually the case that σmu << σfu , it is evident from graphs 2 and 4 that the fibre strength is dominant in determining the axial strength of long-fibre composites.
∴ σ1u ∼ fσfu for all axial cases.
Transverse Strength
In general, the presence of fibres reduces the transverse strength and the failure strain significantly relative to the unreinforced matrix. This observed tendency is largely due to high local stresses and strains around the fibre / matrix interface due to differences in the Young's Moduli of the two components. However, the transverse strength is also influenced by many other factors and consequently, it is not possible to deduce a simple estimate of σ2u without making several approximations.
One approach is to treat the fibres in the composite as a set of cylindrical holes in a simple square array. We then consider the case where the reduction in the composite cross-sectional area is maximum and this leads to the following expression for the transverse strength of a composite having a volume fraction f of fibres:
\[\sigma_{2 u}=\sigma_{m u}\left[1-2\left(\frac{f}{\pi}\right)^{1 / 2}\right]\]
See Transverse strength derivation
Why is this approach inaccurate?
Click here to see Transverse strength inaccuracy.
Shear Strength
Similarly here, we cannot derive a simple expression for the shear strength. There are a total of six combinations of shearing plane and direction that can be grouped into three sets of equivalent pairs, as shown in the diagrams.
Shear directions
τ21 and τ31 are unlikely to occur since these require breaking of the fibres and it is not obvious which of τ12 and τ32 is easier to happen. When considering the stresses on a thin lamina in the 1-2 plane, τ32 is zero and only τ12u is important. Finite difference methods (beyond the scope of this TLP) were used to deduce the variation of the shear stress concentration factor, Ks , with fibre volume fraction.
Here, we will just take the result of this analysis, without proof, to be:
τ12u = Ks τmu
Where τmu is the ultimate matrix shear stress and Ks varies as shown in graph 6. Ks is about 1 unless the fibre volume fraction is very high (> 70%).
τ12u ≈ τmu (9)



