5.2: Nucleation and crystallization
- Page ID
- 7808
Living cells consist essentially of an aqueous solution contained within a cell membrane. Thus the soft tissues of many living systems can be described as structured water. The human body for instance, is 50-75 % water. This high proportion of water means that crystallization in the body occurs in two main ways:
- by dehydration, when minerals crystallize from a saturated solution.
- by freezing, when ice crystals are formed.
The formation of crystals in living cells is usually fatal. This is either due to a change in the ionic ratios in the cytosol or due to the bursting of the cell.
During dehydration, water is removed from the cell, leading to a supersaturated solution. Mineral or sugar crystals can then form, changing the ionic ratios in the cytosol.
Ice crystals can form in the cells of both plants and ectothermic (cold-blooded) animals. Since ice is essentially pure H2O, ice formation can increase the concentration of minerals in the remaining cytosol to a toxic level. The increased mineral concentration in the cytosol will cause water to be drawn in from the surrounding cells by osmosis, which can cause the cell to swell and burst.
In dehydration, the crystals that are formed can puncture the cell membrane causing the cells to burst, leading to death.
Both dehydration and ice formation involve the nucleation and growth of a new, solid phase from an aqueous solution. In the case of ice formation, the situation is effectively that of a solid crystallizing from a melt. In the case of the formation of mineral crystals, the case is that of precipitation from solution. Nucleation is the formation of a small cluster (or nucleus) of the new phase, and these nuclei arise spontaneously. Nuclei that are smaller than a certain size will simply disappear, but if a nucleus is greater than a certain size, it will spontaneously grow and will eventually form a grain. This critical size varies with temperature and the reasons for this are outlined below, using the example of ice forming in water.
Nucleation can occur either homogeneously (nucleation in a uniform phase in which there are no inhomogeneities on which nucleation can preferentially occur) or heterogeneously (in which the new phase nucleates on an inhomogeneity).
For the nucleation of ice in pure water, the transformation is a structural change only (there is no change in the chemical composition), and the change in free energy per unit volume on transformation is ΔGv. The interface between the ice and water phase has a free energy γ per unit area. Due to the random motion of the water molecules, nuclei of ice will continually form. Assuming that these nuclei are spherical with radius r, the work done in forming the nucleus is:
Work for nucleation = change in free energy of bulk phases + interface energy
or
\[W=\frac{4}{3} \pi r^{3} \Delta G_{v}+4 \pi r^{2} \gamma\]
Since the interface between the water and liquid can be considered to be a defect, it contributes an excess energy to the system, and γ is positive. γ is approximately constant over the relevant range of temperatures. ΔGv varies with temperature (as described below), but if the transformation occurs spontaneously, (i.e. if the temperature is below the melting temperature of ice), then ΔGv is negative, and a graph of <W against r has the form:
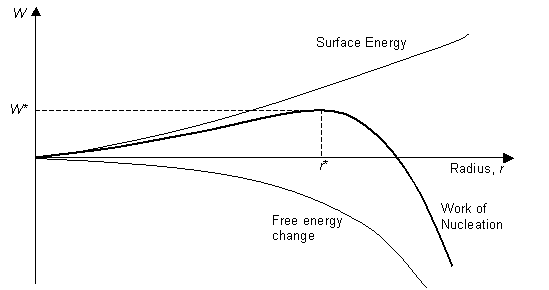
So, if a nucleus is formed, which has r > r*, it will decrease its energy by increasing r, i.e. by growing. Any nuclei with r < r* will decrease in energy by decreasing r and by disappearing. The critical radius, r* occurs when dW/dr = 0, giving:
\[r *=-\frac{2 \sigma}{\Delta G_{v}}\]
and
\[W *=\frac{16 \pi}{3} \frac{\sigma^{3}}{\Delta G_{v}^{2}}\]
We define ΔG to be the free energy difference between the solid and liquid phases, ΔG = ΔGice - ΔGwater. Similarly we define the differences in enthalpy ΔH and entropy ΔS. Since ΔG = ΔH - TΔS and at Tm, the melting point of ice, ΔG = 0, then ΔH = TmΔS. If ΔH and ΔS are independent of temperature, then, at temperature T, ΔG = ΔS(Tm - T) = ΔS ΔT, where ΔT is the supercooling (also known as undercooling). The critical radius and the work for nucleation therefore decrease with decreasing temperature below Tm, and the rate of nucleation would increase with temperature below Tm. This effect is limited by the decrease in atomic mobility at lower temperatures, and the actual variation of nucleation frequency with temperature is shown below:
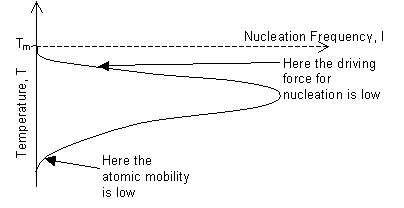
However, this analysis assumes homogeneous nucleation, which occurs only rarely. Usually there are heterogeneities, such as mould walls or cell membranes, in the melt onto which nucleation preferentially occurs. These heterogeneities are points with high excess energy and so the energy required to form the interface between the existing phase and the new phase is not so significant. Removing heterogeneities is one effective way of decreasing the temperature at which ice forms, i.e. increasing the difficulty of freezing.


