3.4: Hook’s Law in Generalized Quantities for Beams
- Page ID
- 21486
There are three generalized forces in beams \((M, N, \nu)\) but only two generalized kinematic quantities \((\epsilon^{\circ}, \kappa)\). There is no generalized displacement on which the shear force could exert work. So the shear force is treated as a reaction in the elementary beam theory. This gives rise to some internal inconsistency in the beam theory, which will be enumerated in a separate section.
The starting point in the derivation of the elasticity law for beams is the Euler-Bernoulli hypothesis,
\[\epsilon(z) = \epsilon^{\circ} + z\kappa\]
and the one-dimensional Hook law, Equation (3.1.1), and the definition of the bending moment and axial force in the beam, Equations (2.2.16-2.2.18). Let’s calculate first the axial force \(N\)
\[N = \int_{A} \sigma_{xx} dA = \int_{A} E \epsilon_{xx}dA = E\int_{A} (\epsilon^{\circ} + z\kappa) dA \\ = E \int_{A} \epsilon^{\circ} dA + E \int_{A} \kappa z dA = E\epsilon^{\circ} \int_{A} dA + E\kappa \int_{A} z dA\]
Note that the strain of the middle axis \(\epsilon^{\circ}\) and the curvature of the beam axis are independent of the \(z\)-coordinate and could be brought in front of the respective integrals. Also \(Q = \int_{A} zdA\) is the static (first) moment of inertia of the cross-section. From the definition of the neutral axis, \(Q = 0\). The expression for the axial force reduces then to
\[N = EA\epsilon^{\circ}\]
where \(EA\) is called the axial rigidity of the beam. We calculate next the bending moment in a similar way
\[N = \int_{A} \sigma_{xx}z dA = \int_{A} E(\epsilon^{\circ} + z\kappa)z dA \\ = E\epsilon^{\circ} \int_{A} z dA + E\kappa \int_{A} z^2 dA\]
Because the first term involving the static moment of inertia vanishes, and the expression for the bending moment becomes
\[M = EI\kappa\]
where EI is called the bending rigidity and
\[I = \int_{A} z^2 dA\]
is the second moment of inertia. For the rectangular cross-section \((b \times h)\)
\[I = \frac{bh^3}{12}\]
The significance of the above derivation is that the bending response is uncoupled from the axial response and vice versa. This property allows to derive the famous stress formula for beams. This is indeed one line derivation
\[\sigma = E\epsilon = E(\epsilon^{\circ} + z\kappa) = E \left(\frac{N}{EA} + \frac{Mz}{EI}\right) \\ \sigma(z) = \frac{N}{A} + \frac{Mz}{I} \label{4.30}\]
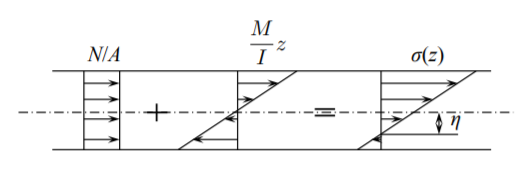
Both axial force and bending moment contribute to the stress distribution along the along the height of the beam, as illustrated in Figure (\(\PageIndex{1}\)).
From Equation \ref{4.30} one can calculate the point \(z = \eta\) where the stresses become zero
\[\eta = − \frac{I}{A}\frac{N}{M} = −\rho^2 \frac{N}{M}\]
where \(\rho\) is the moment of giration of the cross-section defined by \(I = \rho^2A\). The position of the zero stress axis depends on the ratio of axial force to bending moment. If \(\eta < h\), where \(h\) is the thickness of a rectangular section beam, the zero stress point is inside the beam boundary, there is a bending dominated response. The tension dominated response is when \(\eta\) is several times larger than \(h\).


