3.6: Derivation of Constitutive Equations for Plates (Advanced)
- Page ID
- 21488
For convenience, the set of equations necessary to derive the elasticity law for plates is summarized below.
Hook’s law in plane stress reads:
\[\sigma_{\alpha \beta} = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] \label{4.54} \]
In terms of components:
\[\sigma_{xx} = \frac{E}{1 − \nu^2}(\epsilon_{xx} + \nu\epsilon_{yy})\]
\[\sigma_{yy} = \frac{E}{1 − \nu^2}(\epsilon_{yy} + \nu\epsilon_{xx})\]
\[\sigma_{xy} = \frac{E}{1 − \nu} \epsilon_{xy}\]
Here, strain tensor can be obtained from the strain-displacement relations:
\[\epsilon_{\alpha \beta} = \epsilon_{\alpha \beta}^{\circ} + z\kappa_{\alpha \beta}\]
Now, define the tensor of bending moment:
\[M_{\alpha \beta} \equiv \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{\alpha \beta}z dz \label{4.57}\]
and the tensor of axial force (membrane force):
\[N_{\alpha \beta} \equiv \int_{-\frac{h}{2}}^{\frac{h}{2}} \sigma_{\alpha \beta}z dz\]
Bending Moments and Bending Energy
The bending moment \(M_{\alpha \beta}\) is now calculated by substituting Equation \ref{4.54} with Equation \ref{4.57}
\[M_{\alpha \beta} = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] z dz \\ = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} z dz \\ + \frac{E}{1 − \nu^2} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} z^2 dz \\ = \frac{Eh^3}{12(1 − \nu^2)} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}]\]
Note that the term \(\int_{-\frac{h}{2}}^{\frac{h}{2}} z dz \) is zero, as shown in the case of beams. Therefore there are no mid-surface strains \(\epsilon_{\alpha \beta}^{\circ}\) entering the moment-curvature relation.
Here we define the bending rigidity of a plate \(D\) as follows:
\[D = \frac{Eh^3}{12(1 − \nu^2)}\]
Now, one gets the moment-curvature relations in the tensorial form
\[\boxed{ M_{\alpha \beta} = D[(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] }\label{4.61}\]
\[M_{\alpha \beta} = \begin{vmatrix} M_{11} & M_{22} \\ M_{21} & M_{22} \end{vmatrix}\]
where \(M_{12} = M_{21}\) due to symmetry. In the expanded notation,
\[M_{11} = D(\kappa_{11} + \nu\kappa_{22})\]
\[M_{22} = D(\kappa_{22} + \nu\kappa_{11})\]
\[M_{12} = D(1 - \nu)\kappa_{12})\]
One-dimensional Bending Energy Density
Here, we use the hat notation for a function of certain argument, such as:
\[M_{11} = \hat{M}_{11}(\kappa_{11}) \\ = D\kappa_{11}\]
Then, the bending energy density \(\tilde U_b \) reads:
\[\bar U_b = \int_{0}^{\bar{\kappa}} \hat{M}_{11}(\kappa_{11}) d\kappa_{11} \\ = D \int^{\bar{\kappa}_{11}} \kappa_{11} d\kappa_{11} \\ = \frac{1}{2}D(\bar{\kappa}_{11})^2\]
\[\bar U_b = \frac{1}{2}M_{11}\bar{\kappa}_{11}\]
General Case
General definition of the bending energy density reads:
\[\bar U_b = \oint M_{\alpha \beta} d\kappa_{\alpha \beta}\]
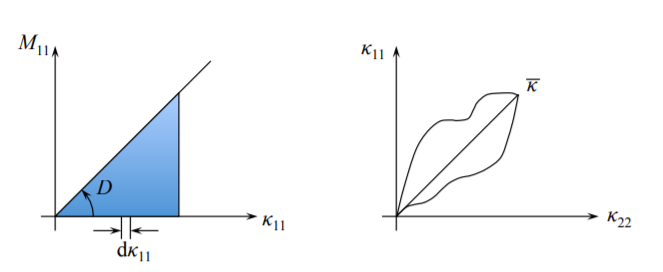
where the symbol \(\oint\) denotes integration along a certain loading path.
Let’s calculate the energy density stored when the curvature reaches a given value \(\bar{\kappa}_{\alpha \beta}\) along a straight loading path:
\[\kappa_{\alpha \beta} = \eta \bar{\kappa}_{\alpha \beta}\]
\[d\kappa_{\alpha \beta} = \bar{\kappa}_{\alpha \beta}d\eta\]
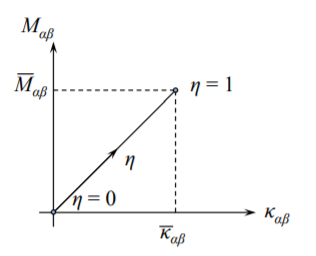
From the linearity of the moment-curvature relation, Equation \ref{4.61}, it follows that
\[M_{\alpha \beta} = \hat{M}_{\alpha \beta}(\kappa_{\alpha \beta}) \\ = \hat{M}_{\alpha \beta}(\eta\bar{\kappa}_{\alpha \beta}) \\ = \eta\hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\]
where \(\hat{M}_{\alpha \beta}(\kappa_{\alpha \beta})\) is a homogenous function of degree one.
\[\bar U_b = \oint \hat{M}_{\alpha \beta}(\kappa_{\alpha \beta}) d\kappa_{\alpha \beta} \\ \int_{0}^{1} \eta \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta}d\eta \\ = \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta} \int_{0}^{1} \eta d\eta \\ \frac{1}{2} \hat{M}_{\alpha \beta}(\bar{\kappa}_{\alpha \beta})\bar{\kappa}_{\alpha \beta} \\ = \frac{1}{2} M_{\alpha \beta} \bar{\kappa}_{\alpha \beta}\]
Now, the bending energy density reads
\[\bar U_b = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta} + \nu\bar{\kappa}_{\gamma \gamma}\delta_{\alpha \beta}] \bar{\kappa}_{\alpha \beta} \\ = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta}\bar{\kappa}_{\alpha \beta} + \nu\bar{\kappa}_{\gamma \gamma}\bar{\kappa}_{\alpha \beta}\delta_{\alpha \beta}] \\ = \frac{D}{2} [(1 − \nu)\bar{\kappa}_{\alpha \beta}\bar{\kappa}_{\alpha \beta} - \nu(\bar{\kappa}_{\gamma \gamma})^2]\]
The bending energy density expressed in terms of components are:
\[\bar U_b = \frac{D}{2} \{(1 - \nu)[(\bar{\kappa}_{11})^2 + 2(\bar{\kappa}_{12})^2 + (\bar{\kappa}_{22})^2] + \nu(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\} \\ = \frac{D}{2} \{(1 - \nu) [(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 ] + \nu(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 - \nu[-2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2]\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2 - \nu[-2\bar{\kappa}_{11}\bar{\kappa}_{22}+ 2(\bar{\kappa}_{12})^2]\} \\ = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 + 2(1-\nu) [-\bar{\kappa}_{11}\bar{\kappa}_{22}+ (\bar{\kappa}_{12})^2]\} \]
\[\boxed{\bar U_b = \frac{D}{2} \{(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2 - 2(1 - \nu)[\bar{\kappa}_{11}\bar{\kappa}_{22} - (\bar{\kappa}_{12})^2]\}}\]
The term in the square brackets is the Gaussian curvature, \(\kappa_G\), introduced in Chapter 1, Equation (1.8.9). Should the Gaussian curvature vanish, as it is often the case in plates, then the bending energy density assumes a very simple form \(\bar U_b = \frac{1}{2} D(\bar{\kappa}_{11} + \bar{\kappa}_{22})^2\).
Total Bending Energy
The total bending energy is the integral of the bending energy density over the area of plate:
\[U_b = \int_{S} \bar{U}_b dA\]
Membrane Forces and Membrane Energy
The axial force can be calculated in a similar way as before
\[N_{\alpha \beta} = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta} + \nu\epsilon_{\gamma \gamma}\delta_{\alpha \beta}] dz \\ = \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] dz \\ + \frac{E}{1 − \nu^2} \int_{-\frac{h}{2}}^{\frac{h}{2}} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] z dz \\ = \frac{E}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} dz \\ + \frac{E}{1 − \nu^2} [(1 − \nu)\kappa_{\alpha \beta} + \nu\kappa_{\gamma \gamma}\delta_{\alpha \beta}] \int_{-\frac{h}{2}}^{\frac{h}{2}} dz \\ = \frac{Eh}{1 − \nu^2} [(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \gamma\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}]\]
The integral \(\int_{-\frac{h}{2}}^{\frac{h}{2}} z dz\) is zero which means that there is no coupling between the membrane force and curvatures.
Here we define the axial rigidity of a plate \(C\) as follows:
\[C = \frac{Eh}{1 − ν^2}\]
Now, one gets the membrane force-extension relation in the tensor notation:
\[\boxed{N_{\alpha \beta} = C[(1 − \nu)\epsilon_{\alpha \beta}^{\circ} + \nu\epsilon_{\gamma \gamma}^{\circ}\delta_{\alpha \beta}]}\]
\[N_{\alpha \beta} = \begin{vmatrix} N_{11} & N_{12} \\ N_{21} & N_{22} \end{vmatrix}\]
where \(N_{12} = N_{21}\) due to symmetry. In components,
\[N_{11} = C(\epsilon_{11}^{\circ} + \nu\epsilon_{22}^{\circ})\]
\[N_{22} = C(\epsilon_{22}^{\circ} + \nu\epsilon_{11}^{\circ})\]
\[N_{12} = C(1 - \nu) \epsilon_{11}^{\circ}\]
Membrane Energy Density
Using the similar definition used in the calculation of the bending energy density, the extension energy (membrane energy) reads:
\[\bar {U}_m = \oint N_{\alpha \beta} d\epsilon_{\alpha \beta}^{\circ}\]
Let’s calculate the energy stored when the extension reaches a given value \(\bar{\epsilon}_{\alpha \beta}^{\circ}\). Consider a straight path:
\[\epsilon_{\alpha \beta}^{\circ} = \eta\bar{\epsilon}_{\alpha \beta}^{\circ}\]
\[d\epsilon_{\alpha \beta}^{\circ} = \bar{\epsilon}_{\alpha \beta}^{\circ} d\eta\]
\[N_{\alpha \beta} = \hat{N}_{\alpha \beta}(\epsilon_{\alpha \beta}^{\circ}) \\ = \hat{N}_{\alpha \beta}(\eta\bar{\epsilon}_{\alpha \beta}^{\circ}) \\ = \eta\hat{N}_{\alpha \beta}(\bar{\epsilon}_{\alpha \beta}^{\circ})\]
where \(\hat{N}_{\alpha \beta}(\epsilon_{\alpha \beta}^{\circ})\) is a homogenous function of degree one.
\[\bar{U}_m = \int_{0}^{\bar{\epsilon}_{\alpha \beta}^{\circ}} \hat{N}_{\alpha \beta} (\epsilon_{\alpha \beta}^{\circ} ) d \epsilon_{\alpha \beta}^{\circ} \\ = \int_{0}^{1} \eta \hat{N}_{\alpha \beta} (\bar{\epsilon}_{\alpha \beta}^{\circ} ) \bar{\epsilon}_{\alpha \beta}^{\circ} d \eta \\
= \frac{1}{2} \hat{N}_{\alpha \beta} ( \bar{\epsilon}_{\alpha \beta}^{\circ} ) \bar{\epsilon}_{\alpha \beta}^{\circ} \\
= \frac{1}{2} N_{\alpha \beta} \bar{\epsilon}_{\alpha \beta}^{\circ}\]
Now, the extension energy reads:
\[\tilde{U}_m = \frac{C}{2} [(1-\nu) \bar{\epsilon}_{\alpha \beta}^{\circ} + \nu \bar{\epsilon}_{\gamma \gamma}^{\circ} \delta_{\alpha \beta} ] \bar{\epsilon}_{\alpha \beta}^{\circ} \\ = \frac{C}{2} [ (1-\nu) \bar{\epsilon}_{\alpha \beta}^{\circ} \bar{\epsilon}_{\alpha \beta}^{\circ} + \nu ( \bar{\epsilon}_{\gamma \gamma}^{\circ} )^{2} ] \]
The extension energy density expressed in terms of components is:
\[\bar{U}_m = \frac{C}{2} \{ (1-\nu) [ ( \bar{\epsilon}_{11}^{\circ})^{2} + 2 (\bar{\epsilon}_{12}^{\circ})^{2} + (\bar{\epsilon}_{22}^{\circ})^{2}] + \nu ( \bar{\epsilon}_{11}^{\circ}+\bar{\epsilon}_{22}^{\circ} )^{2} \} \\
= \frac{C}{2} \{(1-\nu) [ ( \bar{\epsilon}_{11}^{\circ} + \bar{\epsilon}_{22}^{\circ} )^{2} - 2 \bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ}+2 ( \bar{\epsilon}_{12}^{\circ} )^{2} ] + \nu ( \bar{\epsilon}_{11}^{\circ}+\bar{\epsilon}_{22}^{\circ} )^{2} \} \\
= \frac{C}{2} \{ ( \bar{\epsilon}_{11}^{\circ} + \bar{\epsilon}_{22}^{\circ})^{2} - 2 \bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ} + 2 (\bar{\epsilon}_{12}^{\circ})^{2}-\nu [-2 \bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ} + 2 ( \bar{\epsilon}_{12}^{\circ} )^{2} ] \} \\
=\frac{C}{2} \{ ( \bar{\epsilon}_{11}^{\circ} + \bar{\epsilon}_{22}^{\circ} )^{2} + 2(1-\nu) [ -\bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ} + ( \bar{\epsilon}_{12}^{\circ} )^{2} ] \}\]
\[\boxed{\bar{U}_m = \frac{C}{2} \{ (\bar{\epsilon}_{11}^{\circ} + \bar{\epsilon}_{22}^{\circ} )^{2} - 2(1-\nu) [\bar{\epsilon}_{11}^{\circ} \bar{\epsilon}_{22}^{\circ} - (\bar{\epsilon}_{12}^{\circ} )^{2} ] \} }\]
The total membrane energy is the integral of the membrane energy density over the area of plate:
\[U_m = \int_{S} \bar{U}_m dS\]


