5.1: General Formulation

Last updated
Save as PDF

Page ID: 21497

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Compare to the classical theory of beams with infinitesimal deformation, the moderately large deflection theory introduces changes into the strain-displacement relation and vertical equilibrium, but leaves the constitutive equation and horizontal equilibrium unchanged. The kinematical relation, Equation (1.9.5) acquires now a new term due to finite rotations of beam element.

\[\epsilon^{\circ} = \frac{du}{dx} + \boxed{\frac{1}{2} \left(\frac{dw}{dx}\right)^2} − \text{ new term} \label{5.1.1}\]

The definition of curvature has also a nonlinear rotation term

\[\kappa = -\frac{\frac{d^2w}{dx^2}}{\left[ 1+ \left(\frac{dw}{dx}\right)^2\right]^{3/2}} \label{5.1.2}\]

The square of the slope can be large, as compared with the term \(\frac{du}{dx}\) and must be retained in Equation \ref{5.1.1}. At the same time the square of the slope (beam rotation) are small compared to unity. Why? This is explained in Figure (\(\PageIndex{1}\)), where the square of the slope is plotted against the slope.

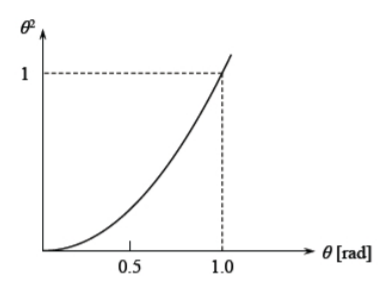
5.1.1.png — Figure \(\PageIndex{1}\): The significance of the square of the slope term.

At \(\theta = 1\) rad \( = 57\) degrees the two terms in the denominator of Equation \ref{5.1.2} are equal. However, the theory of moderately large deflections are valid up to \(\theta = 10^{\circ} \approx 0.175\) rad. The term \(\theta^2\) amounts to \(0.03\), which is negligible compared to unity. Therefore the curvature is defined in the same way as in the theory of small deflections

\[\kappa = -\frac{d^2w}{dx^2}\]

It was shown in Chapter 2 that the equation of equilibrium in the horizontal direction is not affected by the finite rotation. Therefore, we infer from Equation (2.7.4) that the axial force is either constant or zero

\[N = \text{ constant}\]

The vertical equilibrium, given by Equation (3.79) has a new nonlinear term

\[\frac{d^2M}{dx^2} + \boxed{N\frac{d^2w}{dx^2}}^{-\text{new term}} +q = 0\]

Finally, the elasticity law is unaffected by finite rotation

\[N = EA\epsilon^{\circ}\]

\[M = EI\kappa\]

The solution to the coupled problem depends on the boundary conditions in the horizontal direction. Referring to Figure 4.1.1, two cases must be considered:

Case 1, beam free to slide, \(N = 0, \; u \neq 0\).
Case 2, beam fixed, \(u = 0, \; N \neq 0\).