8.5: Stability in Tension

For some materials instability in tension manifest itself by a development of a local neck, Figure (\(\PageIndex{1}\)).

Figure \(\PageIndex{1}\): Necking in a solid section bar and thin-walled tube under tension.

Consider a round bar of the initial cross-sectional area \(A_o\) subjected to a tensile force \(P\). The bar becomes longer and because the Poisson effect its cross-section shrinks to a current value \(A\). The present analysis is valid for materials that are incompressible, that is do not change volume but only shape. Certain polymers, rubber and metals (in the plastic range) are incompressible.

The volume of an infinitesimal length \(l\) is

\[ V = lA \]

The increment of volume for the incompressible material must be equal to zero

\[\delta V = \delta (lA) = \delta lA + l \delta A = 0 \]

Take the logarithmic definition of the axial strain

\[\epsilon = \ln \frac{l}{l_o} ; \quad \delta \epsilon = \frac{\delta l}{l} \]

From the above two equations

\[\delta \epsilon = \frac{\delta l}{l}= − \frac{\delta A}{A} \]

Integrating both sides

\[\epsilon = − \ln A + C \nonumber\]

At \(A = A_o\), \(\epsilon = 0\) so \(C = \ln A_o\).

Therefore, the expression for the axial strain becomes

\[\epsilon = \ln \frac{A_o}{A} = \ln \frac{l}{l_o} \]

We conclude that axial strain can be determined by either measuring the change in length or the change in cross-sectional area. The true (Cauchy) stress is defined as the load divided by the current cross-section \(A\)

\[\sigma = \frac{P}{A} \]

Let’s construct the total potential energy and its first variation

\[\delta \prod = \int_{V} \sigma \delta \epsilon dv − P \delta u \label{9.60}\]

Before instability occurs, the deformation and stress (uniaxial tension) is uniform across the section of the bar of the length \(l\)

\[u = l \epsilon = l \ln \frac{A_o}{A} \label{9.61a}\]

\[\delta u = −l \frac{\delta A}{A} \label{9.61b}\]

Thus, from Equations \ref{9.60} and \ref{9.61a} - \ref{9.61b}

\[\delta \prod = \int_{V} \sigma \delta \epsilon dv + Pl \frac{\delta A}{A} \]

The second variation of the total potential energy is

\[\delta^2 \prod = \int_{V} \delta \sigma \delta \epsilon dv − Pl \frac{\delta A \delta A}{A^2} \]

Applying the Trefftz stability condition \(\delta^2 \prod = 0\) one gets

\[lA \delta \sigma \delta \epsilon = Pl \delta \epsilon \delta \epsilon \]

or

\[\delta \sigma = \frac{P}{A} \delta \epsilon = \sigma \delta \epsilon \]

and finally

\[ \frac{\delta \sigma}{\delta \epsilon} = \sigma \label{9.66}\]

The incompressible bar is losing stability in tension when the local tangent to the stress-strain curve becomes equal to the value of stress at that point. A graphical interpretation is shown in Figure (\(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): The construction of Considere’ who was the first to derive Equation \ref{9.66}.

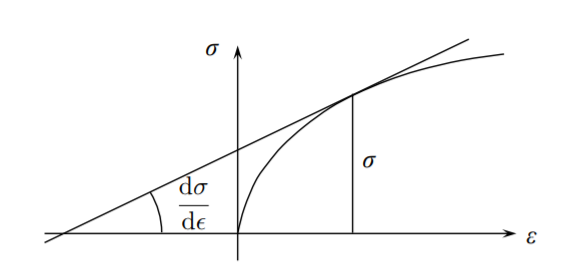
At what strain an instability develops for an elastic material? In uni-axial stress

\[\sigma = E\epsilon \]

\[\frac{d\sigma}{d\epsilon} = E \]

Equation \ref{9.66} is satisfied if \(\epsilon = 1\). For metals such strain is not attainable in the elastic range because yield will be reached at the strain \(\epsilon_y = \frac{\sigma_y}{E} \cong 10^{−3}\). However, for rubber and similar polymeric materials the Young’s modulus is four orders of magnitude smaller, so necking is of common occurrence. The derivation of the instability condition \ref{9.66} was done without any assumption on the stress-strain relation of the material. Therefore this condition is valid for an elastic as well as plastic material. This brings us to the next topic which is plastic buckling of columns.