8.7: Mode Transition (Advanced)
- Page ID
- 21765
Moment Equilibrium Equation
For a pin-pin supported column, the shape of the imperfection \(\bar{w}(x)\) and the deformation \(w(x)\) satisfy the moment equilibrium equation
\[EIw^{\prime \prime} + P w = EI\bar{w}^{\prime \prime} \label{9.77}\]
The solutions should satisfy the boundary conditions
\[\begin{align*} w(0) &= 0 \\[4pt] w^{\prime \prime}(0) &= 0 \\[4pt] w(l) &= 0 \\[4pt] w^{\prime \prime}(l) &= 0 \end{align*}\]
Of course, the solutions should also satisfy the continuous conditions: \(w(x)\) and \(w^{\prime}(x)\) are continuous along the entire length of the column, namely, no step or kink occurs in the solutions.
We can expand the imperfection \(\bar{w}(x)\) in Fourier series as
\[\bar{w}(x) = \sum^{\infty}_{n=1} A_n \sin \frac{n \pi x}{l} \label{9.79}\]
The coefficients \(A_n\) can be determined by Fourier transformation of \(\bar{w}\):
\[A_n = \frac{2}{l} \int_{0}^{l} \bar{w}(x) \sin \frac{n \pi x}{l} dx \]
The deformation \(w(x)\) under a load \(P\) can be written as a summation of a complete set of Fourier series
\[w(x) = \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} \label{9.81}\]
where \(B_n\) can be determined by Equation \ref{9.77}.
Equation \ref{9.77} now becomes
\[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \frac{P}{EI} \sum^{\infty}_{n=1} B_n \sin \frac{n \pi x}{l} = - \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l}\]
To make the equation hold, the coefficients should satisfy
\[−B_n \frac{n^2 \pi^2} {l^2} + \frac{P}{EI} B_n = −A_n \frac{n^2 \pi^2} {l^2} \]
Solve for \(B_n\), we get
\[B_n = A_n \frac{1}{1 − \bar{P}/n^2} \]
here, we defined \(\bar{P} = P/P_c\) and \(P_c = \frac{\pi^2 EI}{l^2}\). So, the deformation \(w(x)\) is
\[w(x) = \sum^{\infty}_{n=1} A_n \frac{1}{1 − \bar{P}/n^2} \sin \frac{n \pi x}{l} \]
The solution tells us what is the shape of the deformation, but it does not tell us any thing about the stability of the equilibrium shape. If we want to study the stability, we have to use potential energy method.
Potential Energy Method
Under a load \(P\), the total potential energy of the column system is (due to Equation (9.2.1) in Chapter 9):
\[\prod = \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \]
Substitute Equations \ref{9.79} and \ref{9.81} into it, we have
\[\begin{align*} \prod &= \frac{EI}{2} \int_{0}^{l} (w^{\prime \prime} − \bar{w}^{\prime \prime})^2 dx − \frac{P}{2} \int_{0}^{l} (w^{\prime 2} − \bar{w}^{\prime 2}) dx \\[4pt] &= \frac{EI}{2} \int_{0}^{l} \left[ -\sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} + \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right)^2 \sin \frac{n \pi x}{l} \right]^2 dx - \frac{P}{2} \int_{0}^{l} \left\{ \left[ \sum^{\infty}_{n=1} B_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 - \left[ \sum^{\infty}_{n=1} A_n \left(\frac{n \pi} {l} \right) \cos \frac{n \pi x}{l} \right]^2 \right\} dx \\[4pt] &= \frac{\pi^4 EI}{4l^3} \sum^{\infty}_{n=1} (B_n - A_n)^2 n^4 - \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} B_n^2 n^2 + \frac{\pi^2 P}{4l} \sum^{\infty}_{n=1} A_n^2 n^2 \\[4pt] &= \frac{\pi^2 P_c}{4l} \left\{ \sum^{\infty}_{n=1} [(B_n - A_n)^2 n^4 - \bar{P} (b_n^2 - a_n^2) n^2] \right\} \end{align*}\]
The orthogonality of Fourier series is used to simplify the integration.
In order to obtain the equilibrium solution, we need the first derivative of potential energy
\[\frac{\partial \prod}{\partial B_n} = 0 \quad \rightarrow \quad B_n = A_n \frac{1}{1 − \bar{P}/n^2} \label{9.88}\]
which is exactly the same as the solution given by solving the equilibrium equation.
To see the stability of the solution, we need the second derivative of potential energy
\[\frac{\partial^ \prod}{\partial B_n^2} > 0 \quad \rightarrow \quad \bar{P} < n^2 \label{9.89}\]
We can see the following points directly from Equations \ref{9.88} and \ref{9.89}:
- The critical buckling load for the \(n^{th}\) mode is \(P_c = \frac{n^2\pi^2 EI}{l^2}\).
- The modes that satisfy \(n^2 > \bar{P}\) are in stable equilibrium.
- For the modes that satisfy \(n^2 < \bar{P}\), we can still solve for a value of \(B_n\), but those modes are unstable and will snap into either plus or minus infinity.
Example \(\PageIndex{1}\)
The imperfection \(\bar{w}(x)\) consists of only the first two modes, namely
\[\bar{w}(x) = A_1 \sin \frac{\pi x}{l} + \sin \frac{2 \pi x}{l} \]
If \(A_1 = 0\), the zero point is at the center of the column. If \(A_1 \neq 0\), the zero point is displaced by a distance \(u\). \(u\) is given by
\[u = \frac{\sin^{−1} \frac{A_1}{2}}{\pi} l , \quad 0 \leq A_1 \leq 2 \]
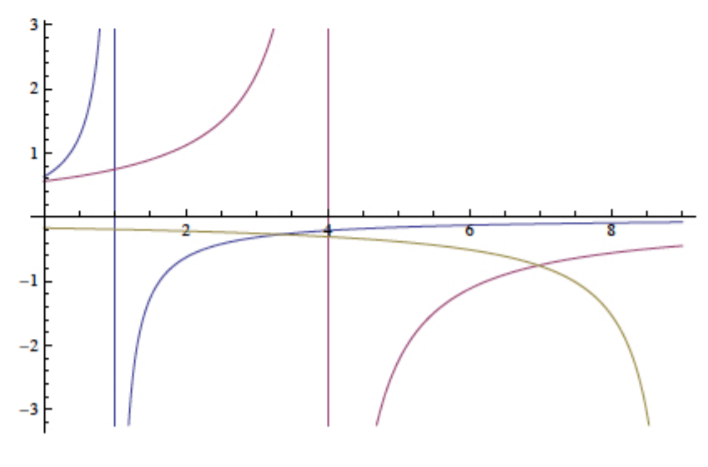
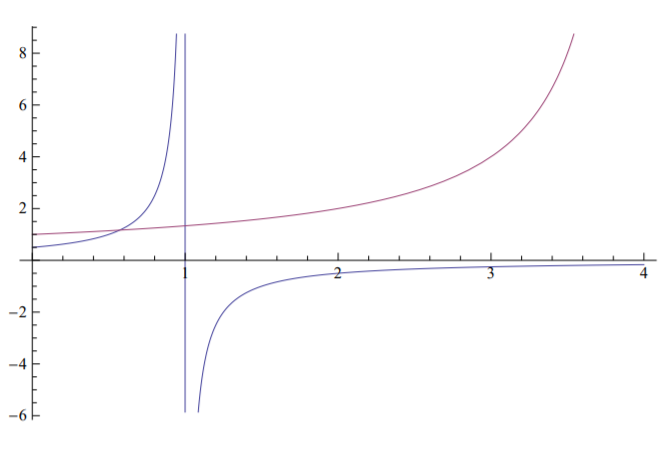
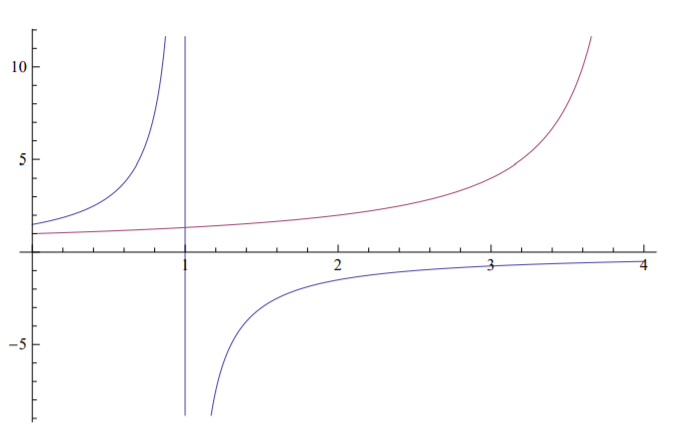
The deformation amplitudes vs. load curves are plotted in Figure (\(\PageIndex{1}\)) for the case \(A_1 = 0.5\), Figure (\(\PageIndex{2}\)) for \(A_1 = 1\), and Figure (\(\PageIndex{3}\)) for \(A_1 = 1.5\).

Example \(\PageIndex{2}\)
The imperfection is in such a shape that the zero point is displaced while both sections are self-symmetric. Such a shape can be described as
\[\bar{w}(x) = \begin{cases} \sin \frac{\pi x}{\eta l} & 0 < x < \eta l \\ − \frac{1 − \eta}{\eta} \sin \frac{\pi(x − \eta l)}{(1 − \eta)l} & \eta l < x < l \end{cases} \label{9.92}\]
where \(0.5 \leq \eta \leq 1\). When \(\eta = 0.7\), \(\bar{w}(x)\) can be expanded in Fourier series as:
\[\bar{w}(x) = 0.634 \sin \frac{\pi x}{l} + 0.563 \sin \frac{2 \pi x}{l} − 0.174 \sin \frac{3 \pi x}{l} + 0.071 \sin \frac{4 \pi x}{l} + \dots \]
As expected, in this case, the first two modes dominate, but there are still higher modes in the expansion.
We plot the mode amplitudes vs. load in Figure (\(\PageIndex{4}\)). If the load \(\bar{P} > 4\), for example, \(\bar{P} = 7.5\), the amplitude of mode III becomes largest. So, the solved deformation shape looks more like mode III, although the initial imperfection seems having nothing to do with mode III. Nevertheless, this shape is very unstable; since \(\bar{P} > 2^2\), both mode I and mode II are in unstable equilibrium. Under such a load, mode I and mode II will amplify exponentially.