9.1: The Tallest Column

In 1757 the Swiss mathematician Leonard Euler presented the famous solution for buckling of a pin-pin column under compressive loading at its end. He also formulated and solved the much more difficult problem of a clamped-free column loaded by its own weight. The practical question was how tall the prismatic column could be before it buckles under its own weight. In order to formulate this problem, the equation of equilibrium of a beam/column in the axial direction must be re-visited. Instead the equation \(N^{\prime} = 0\) or \(N = \)const, we must assume that there is a body force \(q\) per unit length \(q = A\rho\), where \(A\) is the cross-sectional area of the column and \(\rho\) is its mass density. Then, the equilibrium in the axial direction requires that

\[N^{\prime} = q \quad \text{ or } \quad N = qx + C \]

In the coordinate system shown in Figure (\(\PageIndex{1}\)), the axial force must be zero at \(x = l\).

Figure \(\PageIndex{1}\): Column loaded at its tip (left) and loaded by its own weight (right).

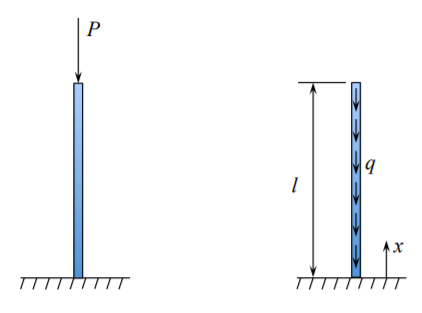
The distribution of axial force along the length of the column is

\[N(x) = −q(l − x) \]

where the minus sign indicates that \(N\) is the compressive force. As before, the input parameters of the problem are \(E\), \(I\) and \(q\) and the unknown is the critical length \(l_c\).

The derivation of the buckling problem for a classical column presented in Chapter 8 is still valid but the axial force in Equation (8.3.11) is no longer constant and thus should be kept inside the integral.

For the present problem the first variation of the total potential energy is

\[\delta \prod = − \int_{0}^{l} M \delta w^{\prime\prime} dx + \int_{0}^{l} q(l − x)w^{\prime} \delta w^{\prime} dx \label{10.3}\]

Integrating the right hand side of Equation \ref{10.3} by part, one gets

\[\int_{0}^{l} M^{\prime\prime} + q(l − x)w^{\prime} \delta w dx + \text{ Boundary terms } = 0 \]

where

\[\text{ Boundary terms } = −\left. M \delta w^{\prime} \right|^{l}_{0} + \left. M^{\prime} \delta w \right|^{l}_{0} + q(l − x) w^{\prime} \delta w \]

at \(x = 0\), \(\delta w = \delta w^{\prime} = 0\); and at \(x = l\), \(M = 0\), \(V = M^{\prime} = 0\) and \(l − x = 0\). Therefore the boundary terms vanish (see the dedication in Section 2.5). Using the elasticity law, \(M = −EIw^{\prime\prime}\), the local equilibrium equation for the column self buckling becomes

\[EI \frac{d^4w}{dx^4} + \frac{d}{dx} \left[ q(l − x) \frac{dw}{dx} \right] = 0 \]

Integrating once, we get

\[EI \frac{d^3w}{dx^3} + q(l − x)dw = 0 \label{10.7}\]

The integration constant is zero because the shear force vanishes at the free end \(x = l\). The governing equation is the third order linear differential equation with a variable coefficient. The solution is no longer represented by the harmonic function. The way to solve the problem is to introduce two new variables

\[\xi = \frac{2}{3} \sqrt{ \frac{q(l − x)^3}{EI}}, \quad u = \frac{dw}{d\xi} \]

Then, Equation \ref{10.7} transforms to the Bessel equation

\[\frac{d^2 u}{d\xi^2} + \frac{1}{\xi} \frac{du}{d\xi} + (1 − \frac{1}{9\xi^2} )u = 0 \]

Omitting the details of the calculation, the critical length of the column is found to be

\[l^3_c = \frac{9EI}{4q} j^2_{\frac{1}{3}} \]

where \(j_{\frac{1}{3}} = 1.866\) is the root of the Bessel function of the third kind. Finally

\[l^3_c = 7.837 \frac{EI}{q} \]

The total weight of the column material is \(N_c = l_cq\). In terms of the total weight, the critical length is

\[l^2_c = 7.84 \frac{EI}{N_c} \label{10.12}\]

For comparison, the length of the free-clamped column at buckling loaded by the same weight is

\[l^2_c = \frac{\pi^2}{4} \frac{EI}{N_c} = 2.47 \frac{EI}{N_c} \]

The bottom of both column sees the same weight, but the critical length of the column undergoing self-buckling is \(\sqrt{\frac{7.84}{2.47}} = 1.78\) times taller than a similar cross-section column loaded at its tip.

Example \(\PageIndex{1}\)

A steel tubular mast solidly built-in the foundation and is free on its top. The cylinder is \(t = 3\) mm thick and has a radius of \(R = 50\) mm. What is the critical length of the mast to buckle under its own weight?

The total weight of the mast is

\[N_c = Al \rho\]

where \(A\) is the cross-sectional area, \(A = 2\pi Rt\). The second moment of inertia of the thinwalled tube is \(I = \pi R^3 t\). From Equation \ref{10.12}

\[l^2_c = 7.84 \frac{E \pi R^3 t}{2 \pi Rtl_c \rho} \]

from which one gets

\[l_c = \sqrt[3]{\frac{3.92ER^2}{\rho}} = 65 m \]

The above solution applies to a prismatic column of a constant cross-section.

Approximate solution can be derived from the Trefftz condition \(\delta^2 \prod = 0\). Starting from Equation \ref{10.3} and performing the second variation one gets

\[EI \int_{0}^{l} \delta w^{\prime\prime} \delta w^{\prime} dx + \int_{0}^{l} q(l − x)\delta w^{\prime} \delta w dx \]

The critical compressive body force is then

\[q = EI \frac{\int_{0}^{l} \phi^{\prime\prime} \phi^{\prime\prime} dx}{\int_{0}^{l} (l − x)\phi^{\prime}\phi^{\prime} dx} \label{10.18}\]

As compared with the standard Trefftz formula for tip loaded column, there is the term \((l − x)\) in the denominator. As an example consider the simplest parabolic deflection shape

\[\phi = x^2 \]

\[\phi^{\prime} = 2x \]

\[\phi^{\prime\prime} = 2 \]

Introducing the above expression into Equation \ref{10.18}, the critical buckling weight per unit length is

\[q = \frac{12EI}{l^3} \]

The error in this approximation is \(\frac{12 − 7.837}{7.837} = 53\%\) which is not good. As a second trial consider a power shape function with a fractional exponent \(\alpha\)

\[\phi = x^{\alpha} \]

\[\phi^{\prime} = \alpha x^{\alpha−1} \]

\[\phi^{\prime\prime} = \alpha(\alpha − 1)x^{\alpha−2} \]

The resulting solution is

\[q = \frac{2EI}{l^3} \frac{\alpha(\alpha − 1)(2\alpha − 1)}{2\alpha − 3} \]

The critical buckling parameter attains a minimums at \(\alpha = 1.75\). The minimum buckling load is

\[q_{\text{min}} = 9.8 \frac{EI}{l^3} \]

The error is slashed by half but it is still large at 25%. In the third attempt, let’s consider the trigonometric function

\[\phi = 1 − \cos \frac{\pi x}{2l} \label{10.24a}\]

\[\phi^{\prime} = \left(\frac{\pi}{2l}\right) \sin \frac{\pi x}{2l} \]

\[\phi^{\prime\prime} = \left( \frac{\pi}{2l} \right)^2 \cos \frac{\pi x}{2l} \label{10.24c}\]

In addition to satisfying clamped kinematic condition at \(x = 0\), the cosine shape gives the zero bending moment at the top. Substituting Equations \ref{10.24a} - \ref{10.24c} into the Trefftz condition, Equation (10.18), the following closed-form solution is obtained

\[q = \frac{EI}{l^3} \frac{\pi^4}{2(\pi^2 − 4)} = 8.29 \frac{EI}{l^3} \]

which differs by only 6% from the exact solution. The true shape of the column which buckles by its own weight is the Bessel function but the trigonometric function provides a very good approximation.

For over 200 years the Euler solution of buckling of a column under its own weight remains unchallenged. In 1960 Keller and Niordson asked the question by how much can the height of the column be increased. If the same volume of material is distributed as a constant cross-section prismatic structure of the radius \(r = 0.1\) m, the length of the column would be

\[l = \frac{V}{\pi r^2} = \frac{1}{\pi 0.1^2} = 32 m \nonumber \]

and the weight per unit length of a still column will be

\[q = \frac{V}{l} = \frac{7.8 \times 10^4}{32} = 24 N/m \nonumber \]

Using Equation \ref{10.12} we can check if such a column will stay or buckle under its own weight

\[l^2_c = 7.84 \frac{EI}{N} \nonumber \]

where \(I = \frac{\pi r^4}{4}\), \(N = V \rho\) and \(E = 2.1 \times 10^{11} N/m^2\). Substituting the above values, the critical length becomes \(l_c = 26\) m. This means that the 32 m prismatic column will buckle and cannot be erected. By shaping the column according to Figure (\(\PageIndex{2}\)) its length can be increase by a factor of \(86/26 = 3.3\).

If the cross-section is variable, this question has led to a very complex mathematical problem. Some aspects of this solution are still studied up to now. The problem is well-posed if the optimal solution is sought under a constant, given volume of the material. There is no simple closed-form solution to the problem so the answer is obtained through numerical optimization, see Figure (\(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): The shape of the tallest column.

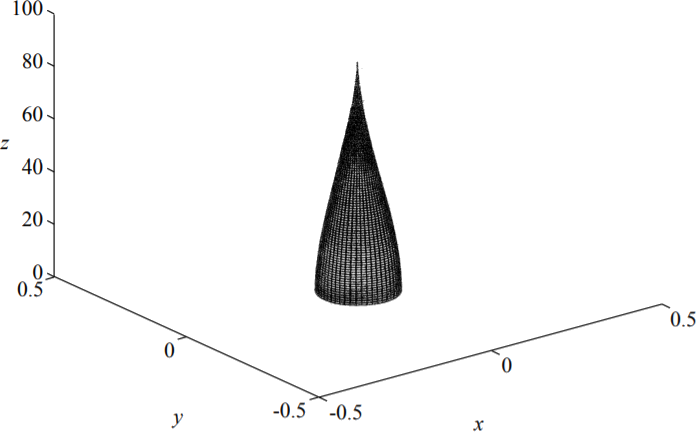
Note that the height of the column was scaled down to fit on the page. To give you an idea, the steel column of the total volume of 1.0 m\(^3\) and the bare radius of 10 cm could be as high as \(l = 86 \) m.