3.4: Moment about a Point (Vector)

Last updated
Save as PDF

Page ID: 50582

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Given any point on an extended body, if there is a force acting on the body that does not travel through that point, then that force will cause a moment about that point. As discussed on the moments page, a moment is a force's tendency to cause rotation.

The Vector Method in 2 and 3 Dimensions

An alternative to calculating the moment via scalar quantities is to use the vector method or cross product method. For simple two-dimensional problems, using scalar quantities is usually sufficient, but for more complex problems the cross product method tends to be easier. The cross product method for calculating moments says that the moment vector of a force about a point will be equal to the cross product of a position vector \(\vec{r}\), from the point to anywhere on the line of action of the force, and the force vector itself. \[ \vec{M} \, = \, \vec{r} \times \vec{F} \]

A big advantage of this method is that \(\vec{r}\) does not have to be the shortest distance between the point and the line of action; it goes from the point to any part of the line of action. For any problem, there are many possible \(\vec{r}\) vectors, but because of the way the cross product works, they should all result in the same moment vector in the end.

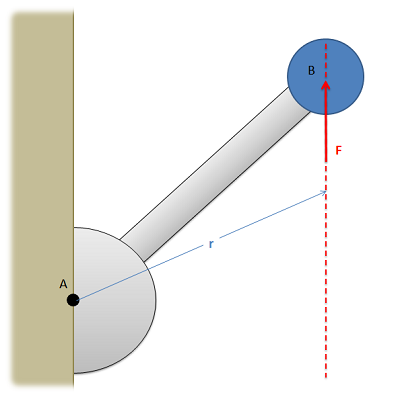
A lever is attached at one end to a wall (point A). An upward force is applied to the free end of the lever, and its extended line of action is drawn; a vector r points from point A to an arbitrary point on the line of action. — Figure \(\PageIndex{1}\): The moment vector of the force \(F\) about point A will be equal to the cross products of the \(r\) vector and the force vector. \(\vec{r}\) is a vector from point A to any point along the line of action of the force.

It is important to note here that all quantities involved are vectors: \(\vec{r}, \, \vec{F}\), and \(\vec{M}\). Before you can solve for the cross product, you will need to write out \(\vec{r}\) and \(\vec{F}\) in vector component form. You will need to write out all three components of these vectors: for two-dimensional problems their \(z\) components will simply be zero, but those values are necessary for the calculations.

The moment vector you get will line up with the axis of rotation for the moment, where you can use the right-hand rule to determine if the moment is going clockwise or counterclockwise about that axis.

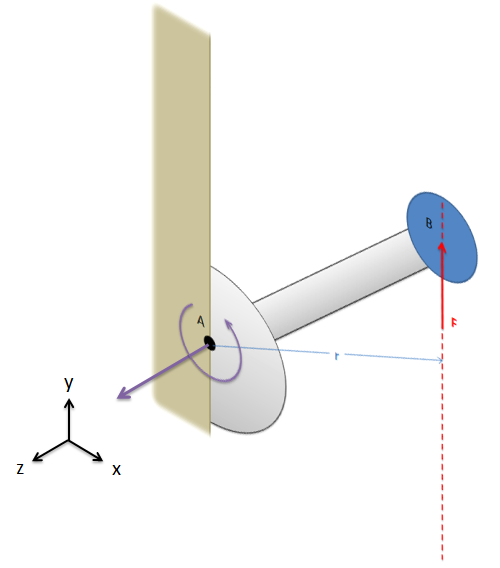
Diagram shows how the direction of a moment can be found by using the right-hand rule, with the example of a counterclockwise rotation in the plane of the screen corresponding to a moment vector pointing out of the screen. — Figure \(\PageIndex{2}\): The result of \(\vec{r} \times \vec{F}\) will give us the moment vector. For this two-dimensional problem, the moment vector is pointing in the positive \(z\) direction. We can use the right-hand rule to determine the direction of rotation from the moment: line our right thumb up with the moment vector and our curled fingers will point in the direction of rotation from the moment.

Finally, it is also important to note that taking the cross product, unlike multiplication, is not communicative. This means that the order of the vectors matters, and \(\vec{r} \times \vec{F}\) will not be the same as \(\vec{F} \times \vec{r}\). It is important to always use \(\vec{r} \times \vec{F}\) when calculating moments.

Video lecture covering this section, delivered by Dr. Jacob Moore. YouTube source: https://youtu.be/Jt2AE2yZFEQ.

Example \(\PageIndex{1}\)

What is the moment that this force exerts about point A? What is the moment this force exerts about point B?

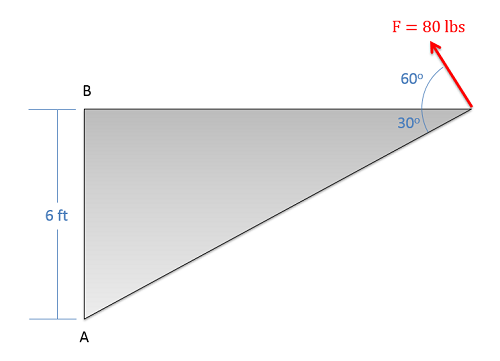A right triangle is oriented so its right angle, point B, is at the top left of the image; point A is one of the corners of the triangle, 6 feet below B. The third angle of the triangle measures 30 degrees; a force of magnitude 80 lbs is applied at that corner, perpendicular to the hypotenuse and pointing up and to the left. — Figure \(\PageIndex{3}\): problem diagram for Example \(\PageIndex{1}\). A force is applied to one corner of a right triangle, producing moments about the triangle's other corners.

Solution: Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/wn1xJZMpDY4.

Example \(\PageIndex{2}\)

Determine the moment that the tension in the cable exerts about the base of the pole (leave the moment in vector form). What is the magnitude of the moment the tension exerts about this point?

A cable with a tension force of 3000 lbs connects the top of an upright 15-foot-high pole to the ground. The location where the end of the cable touches the ground is 15 feet behind the spot that is 3 feet to the right of the base of the pole. — Figure \(\PageIndex{4}\): problem diagram for Example \(\PageIndex{2}\); a three-dimensional arrangement of an upright pole and a cable that connects the pole to the ground.

Solution: Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/ioqy98jZ0Vg.