7.8: Chapter 7 Homework Problems

Last updated
Save as PDF

Page ID: 53946

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exercise \(\PageIndex{1}\)

A car with an initial velocity of 30 m/s accelerates at a constant rate of 12 m/s² . Find the time required for the car to reach a speed of 60 m/s, and the distance traveled during this time.

Solution

Time = \(2.5 \, s\)

Distance = \(112.5 \, m\)

Exercise \(\PageIndex{2}\)

A car traveling at 60 miles per hour approaches a fallen log in the road 400 feet away. Assuming the driver immediately slams on the brakes, what is the required rate of deceleration needed to assure the driver does not hit the log?

Solution: Minimum acceleration: \(-9.68 \, ft/s^2\)

Exercise \(\PageIndex{3}\)

A train experiences the acceleration over time detailed below. Draw the velocity-time and position-time diagrams with all key points and equations labeled, and determine the total distance traveled by the train.

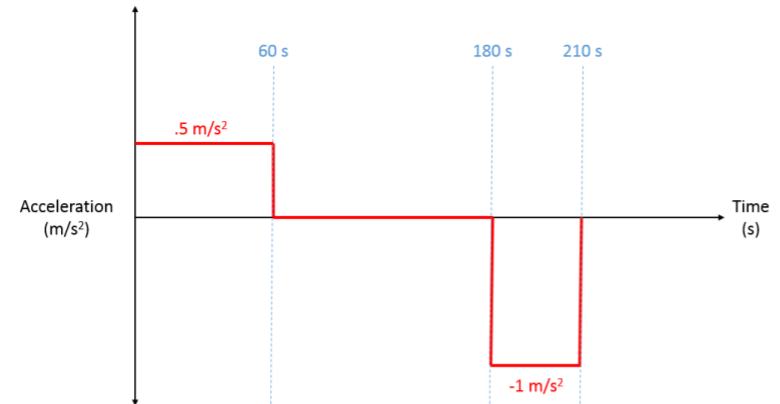Graph of a train's acceleration over time. The acceleration is a constant 0.5 m/s² for the first 60 seconds, then a constant 0 m/s² until the 180-second mark, then a constant -1 m/s² until the 210-second mark. — Figure \(\PageIndex{1}\): problem diagram for Exercise \(\PageIndex{3}\). Graph of a train's acceleration in m/s² over a 210-second period.

Solution: Total distance = \(4950 \, m\), plus v-t and s-t diagrams

Exercise \(\PageIndex{4}\)

As a roller coaster cart comes into the gate at the end of the ride, it goes through two sets of brakes. The cart's velocity over time is shown in the graph below. Draw the acceleration-time and position-time diagrams with all key points and equations labeled. Determine the total distance the cart travels during this seven-second period.

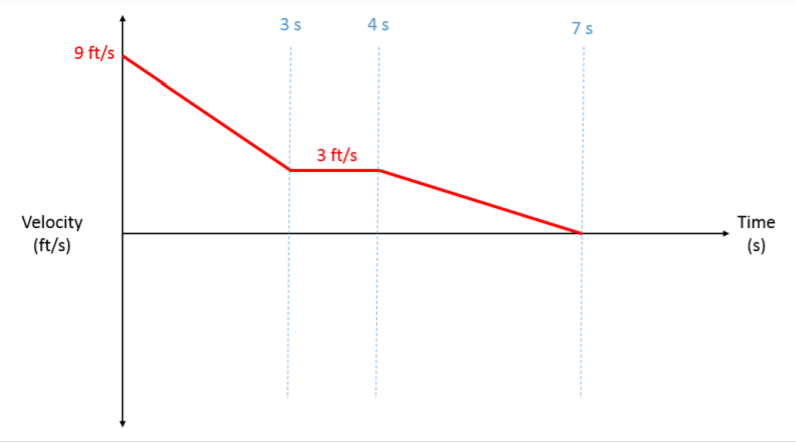Graph of a roller coaster cart's velocity in ft/s over time in seconds. At t=0 the velocity is 9 ft/s; it decreases steadily to reach 3 ft/s at the 3-second mark and remains at that value for 1 second. From t=4 to t=7 seconds, the velocity decreases steadily to 0 ft/s. — Figure \(\PageIndex{2}\): problem diagram for Exercise \(\PageIndex{4}\). Graph of a roller coaster cart's velocity in ft/s over a 7-second period.

Solution: Total distance = \(25.5 \, ft\), plus a-t and s-t diagrams.

Exercise \(\PageIndex{5}\)

A tank fires a round at a 30-degree angle with a muzzle velocity of 600 m/s. The round is expected to hit a mountainside one kilometer away. The mountainside also has an average angle of 30 degrees. How far up the mountainside will the round be expected to travel before hitting the ground \((d)\) if we ignore air resistance?

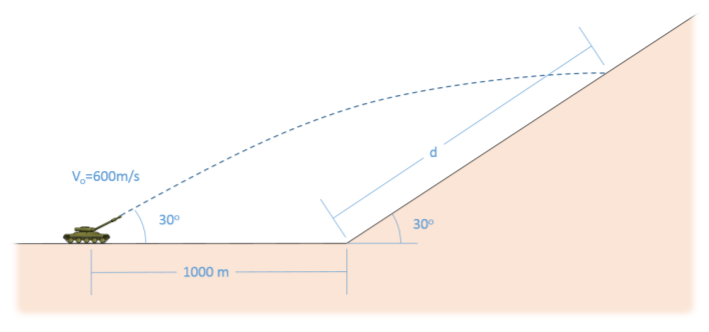A tank is located 1000 meters to the left of the foot of a mountainside that has an incline of 30 degrees. The tank aims at the mountainside and fires a round with an initial velocity of 600 m/s at a 30-degree angle above the horizontal. The path the round is expected to take is traced out with a dotted line, and the point where it impacts the mountain is connected to the foot of the mountain by a distance of d. — Figure \(\PageIndex{3}\): problem diagram for Exercise \(\PageIndex{5}\). A tank fires a round at an angle, aiming towards a mountainside 1 kilometer away.

Solution: \(d = 5.37 \, km\)

Exercise \(\PageIndex{6}\)

A plane with a current speed of 600 ft/s is increasing in speed while also making a turn. The acceleration is measured at 40 ft/s² at an angle 35° from its current heading. Based on this information, determine the rate at which the plane is increasing its speed (tangential acceleration) and the radius of the turn for the plane.

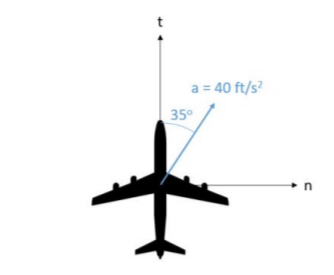Top-down view of a plane pointing straight towards the top of the image (along the t-axis). The n-axis points directly to the right of the image. An acceleration vector for the plane has a magnitude of 40 ft/s² and is 35° to the right of the t-axis. — Figure \(\PageIndex{4}\): problem diagram for Exercise \(\PageIndex{6}\). A plane depicted in a normal-tangential coordinate system undergoes an acceleration that changes both its speed and its direction.

Solution

\(a_t = 32.77 \, ft/s^2\)

\(r = 15,690 \, ft\)

Exercise \(\PageIndex{7}\)

A radar station is tracking a rocket with a speed of 400 m/s and an acceleration of 3 m/s² in the direction shown below. The rocket is 3.6 km away (\(r\) = 3600 m) at an angle of 25°. What would you expect \(\dot{r}\), \(\ddot{r}\), \(\dot{\theta}\), and \(\ddot{\theta}\) to be?

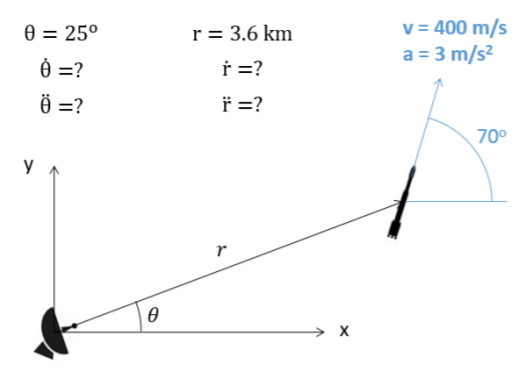The first quadrant of a Cartesian coordinate plane shows a radar station at the origin and a rocket a distance of 3.6 km away from the origin, 25 degrees above the x-axis. The rocket has a velocity vector of magnitude 400 m/s and an acceleration vector of 3 m/s², with both vectors pointing up and to the right at an angle of 70 degrees above the horizontal. — Figure \(\PageIndex{5}\): problem diagram for Exercise \(\PageIndex{7}\). A radar station tracks the instantaneous velocity and acceleration of a rocket located a known distance and angle away.

Solution

\(\dot{r} = 282.8 \,\, m/s, \, \ddot{r} = 24.34 \,\, m/s^2\)

\(\dot{\theta} = 0.0786 \,\, rad/s, \, \ddot{\theta} \,\, -0.01176 \, rad/s^2\)

Exercise \(\PageIndex{8}\)

The pulley system below is being used to lift a heavy load. Assuming the end of the cable is being pulled at a velocity of 2 ft/s, what is the expected upwards velocity of the load?

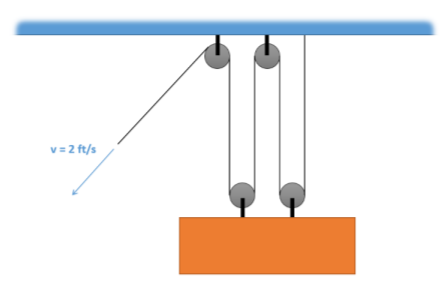Two pulleys of the same size are mounted on a ceiling, and two identical pulleys are attached to the top of a large load. A rope has its right end fastened to the right side of the ceiling and runs down through the right pulley on the load, up through the right pulley on the ceiling, down through the left load pulley, and up through the left ceiling pulley. The dangling left end is pulled downwards at 2 ft/s. — Figure \(\PageIndex{6}\): problem diagram for Exercise \(\PageIndex{8}\). A rope's right end is fastened to the ceiling, and it runs alternately through two pulleys mounted on a load and two pulleys mounted on the ceiling. The left end of the rope is pulled down to raise the load.

Solution: \(v_L = 0.5 \, ft/s\)

Exercise \(\PageIndex{9}\)

A cable is anchored at A, goes around a pulley on a movable collar at B, and finally goes around a pulley at C as shown below. If the end of the rope is pulled with a velocity of 0.5 m/s, what is the expected velocity of the collar at this instant?

A vertical post extends from a ceiling, and holds a movable collar to which a pulley is attached at point B. A rope is attached to the ceiling at point A, 2 meters to the left of the post, runs through the pulley at B (currently 3 meters below the ceiling), and runs through a pulley mounted on the ceiling at point C, 2 meters to the right of the post. The right end of the rope hangs below C and is pulled downwards at 0.5 m/s. — Figure \(\PageIndex{7}\): problem diagram for Exercise \(\PageIndex{9}\). A rope attached to the ceiling at one end runs through a pulley mounted on a sliding collar mounted on a post extending from the ceiling, and then through a pulley mounted on the ceiling. The free rope's free end is pulled downward, moving the collar.

Solution: \(v_B = 0.3 \, m/s\)

Exercise \(\PageIndex{10}\)

You are driving at a velocity of 90 ft/s in the rain while you notice that the rain is hitting your car at an angle 35° from the vertical, from your perspective. Assuming the rain is actually coming straight down (when observed by a stationary person), what is the velocity of the rain with respect to the ground?

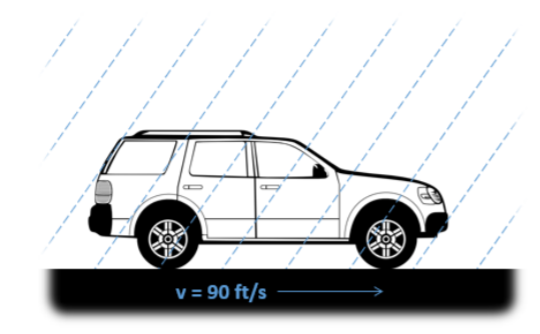Side view of a car moving towards the right at 90 ft/s. Short dashes that represent raindrops are collected into diagonal dashed lines that cross the image from the upper right to the bottom left. — Figure \(\PageIndex{8}\): problem diagram for Exercise \(\PageIndex{10}\). Illustration of the rain's motion as seen from the perspective of a person in the car.

Solution: \(v_r = 128.5 \, ft/s\)