9.1: Conservation of Energy for Particles
- Page ID
- 50606
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The concepts of work and energy provide the basis for solving a variety of kinetics problems. Generally, this method is called the Energy Method or the Conservation of Energy, and it can be boiled down to the idea that the work done to a body will be equal to the change in energy of that body. Dividing energy into kinetic and potential energy pieces as we often do in dynamics problems, we arrive at the following base equation for the conservation of energy.
\[ W = \Delta KE + \Delta PE \]
It is important to notice that unlike Newton's Second Law, the above equation is not a vector equation. It does not need to be broken down into components which can simplify the process. However, we only have a single equation and therefore can only solve for a single unknown, which can limit the method.
Work:
To understand how to use the energy method we first need to understand the concepts of work and energy. Work in general is a force exerted over a distance. If we imagine a single, constant force pushing a body in a single direction over some distance, the work done by that force would be equal to the magnitude of that force times the distance the body traveled. If we have a force that is opposing the travel (such as friction), it would be negative work.
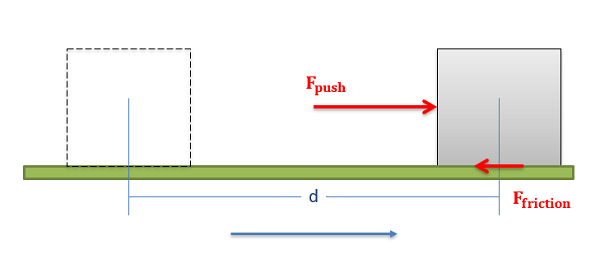
\[ W_{push} = F_{push} * d \]
\[ W_{friction} = - F_{friction} * d \]
For instances where forces and the direction of travel do not match, the component of the force in the direction of travel is the only piece of the force that will do work. Following through with this logic, forces that are perpendicular to the direction of travel for a body will exert no work on a body because there is no component of the force in the direction of travel.
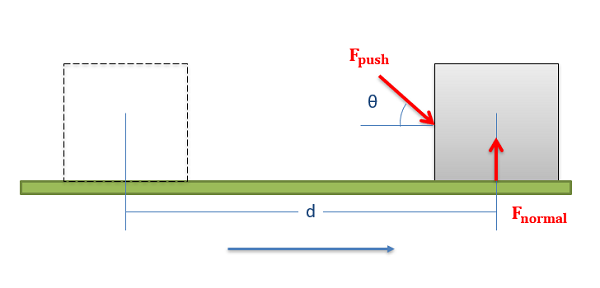
\[ W_{push} = F_{push} \cos (\theta) * d \]
\[ W_{normal} = 0 \]
In the case of a force that does not remain constant, we will need to account for the changing force. To do this we will simply integrate the force function over the distance traveled by the body. Just as before, only the component of the force in the direction of travel will count towards the work done, and forces opposing travel will be negative work.
\[ W = \int\limits_{x_1}^{x_2} F(x) \, dx \]
Energy:
When discussing energy in engineering dynamics, we will usually break energy down into kinetic energy and potential energy. Kinetic energy is the the energy mass in motion, while potential energy represents the energy that is stored up due to the position or stresses in a body.
In its equation form, the kinetic energy of a particle is represented by one half of the mass of the body times its velocity squared. If we wish to determine the change in kinetic energy, we would simply take the final kinetic energy minus the initial kinetic energy.
\[ KE = \frac{1}{2} m v^2 \]
\[ \Delta KE = \frac{1}{2} m v_f^2 - \frac{1}{2} m v_i^2 \]
As a note, a body that is rotating will also have rotational kinetic energy, but we will save that for our discussion of work and energy with rigid bodies.
Potential energy, unlike kinetic energy, is not really energy at all. Instead, it represents the work that a given force will potentially do between two instants in time. Potential energy can come in many forms, but the two we will discuss here are gravitational potential energy and elastic potential energy. These represent the work that the gravitational force and a spring force will do, respectively. We often use these potential energy terms in place of the work done by gravity or springs. When including these potential energy terms, it's important to not additionally include the work done by gravity or spring forces.
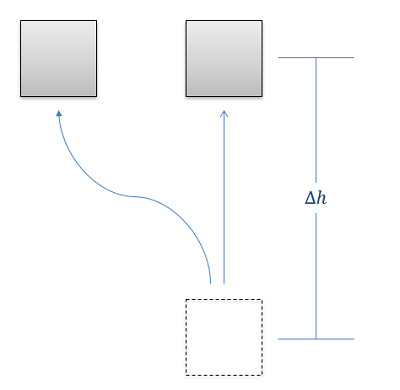
The change in gravitational potential energy for any system is represented by the product of the mass of the body, the value \(g\) (9.81 m/s2 or 32.2 ft/s2 on the earth's surface), and the vertical change in height between the start position and the end position. In equation form, this is as follows.
\[ \Delta PE_{gravity} = m * g * \Delta h \]
To find the change in elastic potential energy, we will need to know the stiffness of the spring (represented by \(k\), in units of force per distance) as well as the distance the spring has been stretched or compressed from its natural resting length (represented by \(x\), in units of distance). Once we have those values, the elastic potential energy can be calculated by multiplying one half of the stiffness by the square of the distance \(x\). To find the change in elastic potential energy, we simply take the final elastic potential energy and subtract the initial elastic potential energy.
\[ \Delta PE _{spring} = \frac{1}{2} k x_f^2 - \frac{1}{2} k x_i^2 \]
Going back to our original conservation of energy equation, we simply plug the appropriate terms on each side (work on the left and energies on the right) and balance the two sides to solve for any unknowns. Terms that do not exist or do not change, such as elastic potential energy in a problem with no springs or \(\Delta KE\) in a problem where there is no change in the speed of the body, can be set to zero.
Example \(\PageIndex{1}\)
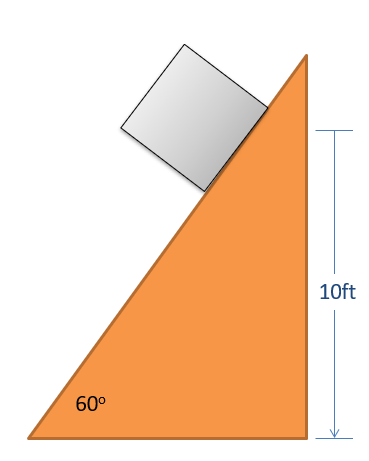
A 16-pound crate slides down a ramp as shown below. The crate is released from a height of 10 feet above the ground.
- What is the work done by gravity?
- What is the change in gravitational potential energy?
- Solution
-
Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\). YouTube source: https://youtu.be/ZkopO1aTj54.
Example \(\PageIndex{2}\)
A spring with an unstretched length of 40 cm and a \(k\) value of 120 N/cm is used to lift a 5-kg box from a height of 20 cm to a height of 30 cm. If the box starts at rest, what would you expect the final velocity to be?
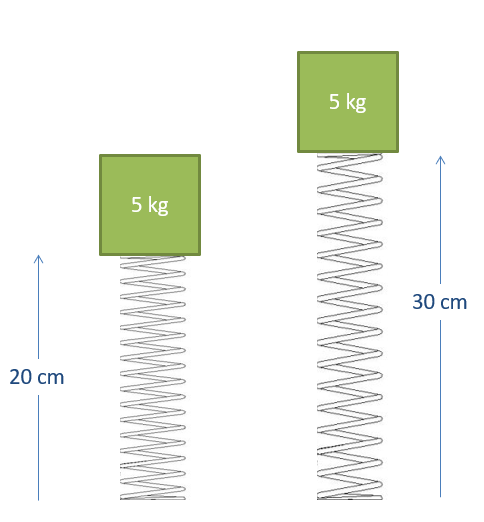
- Solution
-
Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\). YouTube source: https://youtu.be/T_5JT4XFQN8.
Example \(\PageIndex{3}\)
A 2,000-pound wrecking ball hangs from the end of a 40-foot cable. If the wrecking ball is released from an angle of 40 degrees from vertical, what would the expected maximum velocity at the bottom point of the travel path be?
- Solution
-
Video \(\PageIndex{4}\): Worked solution to example problem \(\PageIndex{3}\). YouTube source: https://youtu.be/UkcpT1lfIDY.
Example \(\PageIndex{4}\)
A 24,000-kilogram aircraft is launched from an aircraft carrier using a hydraulic catapult. If the force the catapult exerts over the 90-meter runway is shown in the graph below:
- What is the work done by the catapult?
- What is the speed of the plane at the end of the runway?
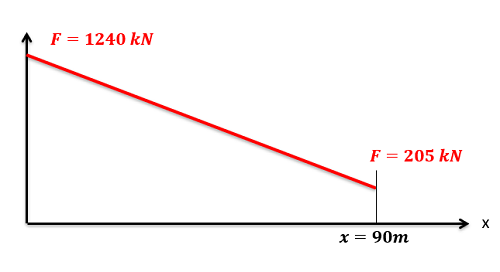
- Solution
-
Video \(\PageIndex{5}\): Worked solution to example problem \(\PageIndex{4}\). YouTube source: https://youtu.be/DfSMeUm1SG8.