15.2: Viscous Damped Free Vibrations

Viscous damping is damping that is proportional to the velocity of the system. That is, the faster the mass is moving, the more damping force is resisting that motion. Fluids like air or water generate viscous drag forces.

Figure \(\PageIndex{1}\): A diagram showing the basic mechanism in a viscous damper. As the system (mass) attached to the loop at the top vibrates up and down, the damper will resist motion in both directions due to the piston passing through the fluid. Image by Egmason, CC-BY SA.

We will only consider linear viscous dampers, that is where the damping force is linearly proportional to velocity. The equation for the force or moment produced by the damper, in either \(x\) or \(\theta\), is:

\[ \vec{F}_c = c \vec{\dot{x}}, \]

\[ \vec{M}_c = c \vec{\dot{\theta}}, \]

where \(c\) is the damping constant. This is a physical property of the damper based on the type of fluid, size of the piston, etc. Note that the units of \(c\) change depending on whether it is damping linear motion (N-s/m) or rotational motion (N-m s/rad).

Figure \(\PageIndex{2}\): Diagram of a hanging mass-spring system, with a linear viscous damper, in equilibrium position. The spring is stretched from its natural length.

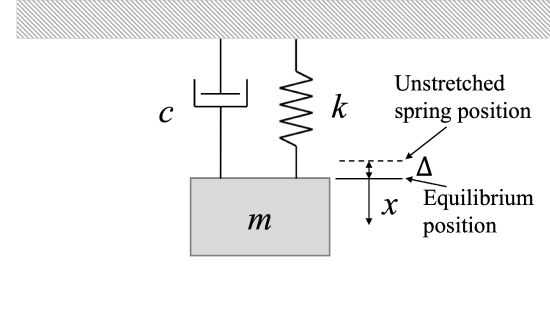
When the system is at rest in the equilibrium position, the damper produced no force on the system (no velocity), while the spring can produce force on the system, such as in the hanging mass shown above. Recall that this is the equilibrium position, but the spring is NOT at its unstretched length, as the static mass produces an extention of the spring.

Figure \(\PageIndex{3}\): Free body diagram of the system in equilibrium position. The spring is at its equilibrium position, but it is stretched and does produce a force.

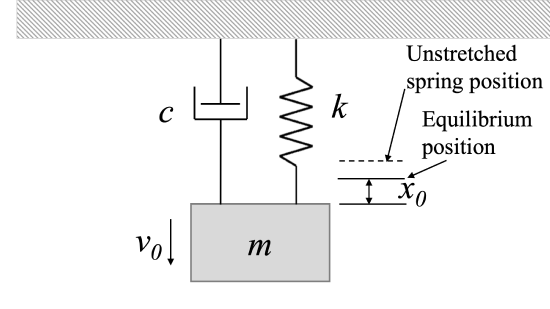
If we perturb the system (applying an initial displacement, an initial velocity, or both), the system will tend to move back to its equilibrium position. What that movement looks like will depend on the system parameters (\(m\), \(c\), and \(k\)).

Figure \(\PageIndex{4}\): The system in a perturbed position. The spring is stretched further and the damper is extended, compared to their equilibrium positions.

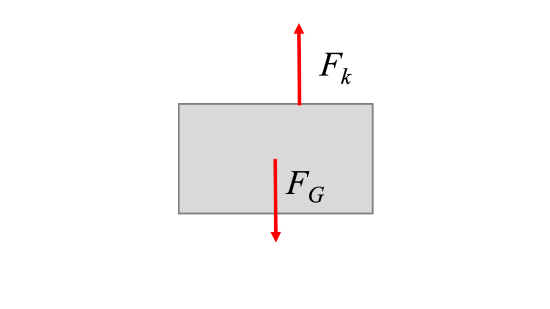
To determine the equation of motion of the system, we draw a free body diagram of the system with perturbation and apply Newton's Second Law.

Figure \(\PageIndex{5}\): Free body diagram of the system with perturbation.

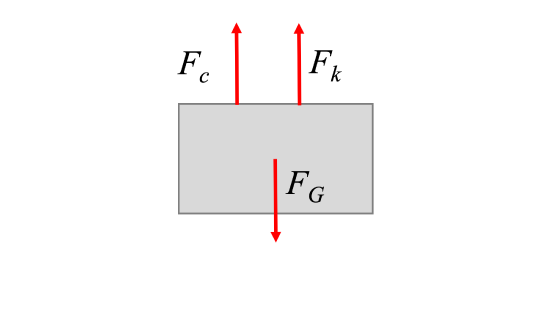
The process for finding the equation of motion of the system is again:

1. Sketch the system with a small positive perturbation (\(x\) or \(\theta\)).
2. Draw the free body diagram of the perturbed system. Ensure that the spring force and the damper force have directions opposing the perturbation.
3. Find the one equation of motion for the system in the perturbed coordinate using Newton's Second Law. Keep the same positive direction for position, and assign positive acceleration in the same direction.
4. Move all terms of the equation to one side, and check that all terms are positive. If all terms are not positive, there is an error in the direction of displacement, acceleration, and/or spring or damper force.

For the example system above, with mass \(m\), spring constant \(k\) and damping constant \(c\), we derive the following:

\[ \sum F_x = m a_x = m \ddot{x} \]

\[ -F_k - F_c = m \ddot{x} \]

\[ -kx - \dot{c(x)} = m \ddot{x} \]

\[ m \ddot{x} + \dot{c(x)} + kx = 0 \]

This gives us a differential equation that describes the motion of the system. We can rewrite it in normal form:

\[ m \ddot{x} + c \dot{x} + kx = 0 \]

\[ \Rightarrow \ddot{x} + \frac{c}{m} \dot{x} + \frac{k}{m} x = 0 \]

\[ \Rightarrow \ddot{x} + 2 \zeta \omega_n \dot{x} + \omega_n^2 x = 0 \]

As before, the term \(\omega_n\) is called the angular natural frequency of the system, and has units of rad/s.

\[ \omega_n ^2 = \frac{k}{m}\, ; \quad \omega_n = \sqrt{\frac{k}{m}} \]

\(\zeta\) (zeta) is called the damping ratio. It is a dimensionless term that indicates the level of damping, and therefore the type of motion of the damped system.

\[ \zeta = \frac{c}{c_c} = \frac{\text{actual damping}}{\text{critical damping}} \]

The expression for critical damping comes from the solution of the differential equation. The solution to the system differential equation is of the form

\[ x(t) = a e^{rt}, \]

where \(a\) is constant and the value(s) of \(r\) can be can be obtained by differentiating this general form of the solution and substituting into the equation of motion.

\[ m r^2 e^{rt} + c r e^{rt} + k e^{rt} = 0 \]

\[ \Rightarrow (mr^2 + cr + k) e^{rt} = 0 \]

Because the exponential term is never zero, we can divide both sides by that term and get:

\[ m r^2 + cr + k = 0. \]

Using the quadratic formula, we can find the roots of the equation:

\[ r_{1,2} = \frac{-c \pm \sqrt{c^2 - 4mk}}{2m} \]

Critical damping occurs when the term under the square root sign equals zero:

\[ c_c ^2 = 4 mk \]

\[ c_c = 2 \sqrt{mk} = 2 m \omega_n \]

Four Viscous Damping Cases:

There are four basic cases for the damping ratio. For the solutions that follow in each case, we will assume that the initial perturbation displacement of the system is \(x_0\) and the initial perturbation velocity of the system is \(v_0\).

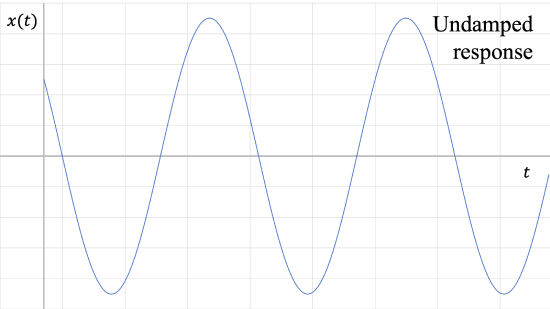
1. \(\zeta = 0\): Undamped

\[ c = 0 \]

This is the case covered in the previous section. Undamped systems oscillate about the equilibrium position continuously, unless some other force is applied.

Figure \(\PageIndex{6}\): Response of an undamped system.

2. \(\zeta > 1\): Overdamped

\[ c^2 > 4 mk \]

Roots are both real and negative, but not equal to each other. Overdamped systems move slowly toward equilibrium without oscillating.

Figure \(\PageIndex{7}\): Response of an overdamped system.

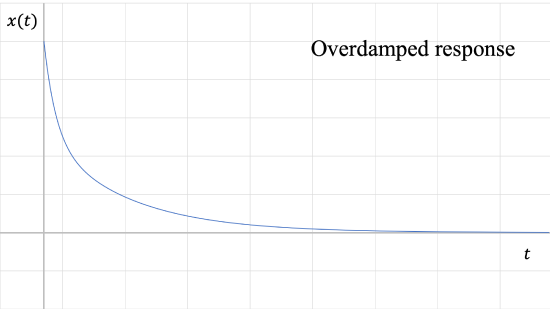
The response for an overdamped system is:

\[ x(t) = a_1 e^{ \left( \frac{-c + \sqrt{c^2 - 4mk}}{2m} \right) t} + a_2 e^{ \left( \frac{-c - \sqrt{c^2 - 4mk}}{2m} \right) t}, \]

\[ \text{where} \,\, a_1 = \frac{-v_0 + r_2 x_0}{r_2 - r_1} \,\, \text{and} \,\, a_2 = \frac{v_0 + r_1 x_0}{r_2 - r_1}. \]

3. \(\zeta = 1\): Critically damped

\[ c^2 = 4 mk ( = c_c^2) \]

Roots are real and both equal to \(- \omega_n\). Critically-damped systems will allow the fastest return to equilibrium without oscillation.

Figure \(\PageIndex{8}\): Response of an critically-damped system.

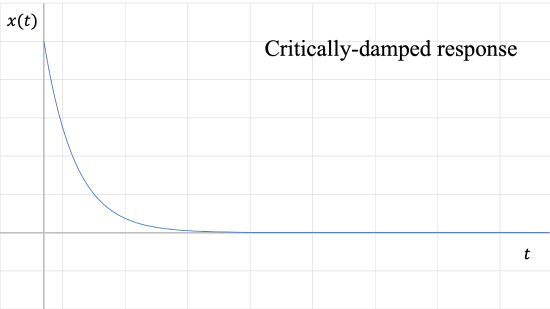
The solution for a critically-damped system is:

\[ x(t) = (A + Bt) e^{-\omega_n t} , \]

\[ \text{where} \,\, A = x_0 \,\, \text{and} \,\, B = v_0 + x_0 \omega_n. \]

4. \(\zeta < 1\): Underdamped

\[ c^2 < 4 mk \]

The roots are complex numbers. Underdamped systems do oscillate around the equilibrium point; unlike undamped systems, the amplitude of the oscillations diminishes until the system eventually stops moving at the equilibrium position.

Figure \(\PageIndex{9}\): Response of an underdamped system.

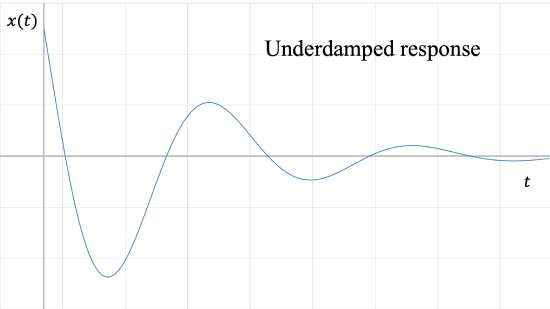
The solution for an underdamped system is:

\[ x(t) = [ C_1 \sin (\omega_d t) + C_2 \cos (\omega_d t) ] e^{- \omega_n \zeta t} , \]

\[ \text{where} \,\, C_1 = \frac{v_0 + \omega_n \zeta x_0}{\omega_d}, \,\, C_2 = x_0, \,\, \text{and} \,\, \zeta = \frac{c}{2 m \omega_n}. \]

\(\omega_d\) is called the damped natural frequency of the system. It is always less than \(\omega_n\):

\[ \omega_d = \omega_n \sqrt{1 - \zeta^2}. \]

The period of the underdamped response differs from the undamped response as well.

\[ \text{Undamped:} \quad \tau_n = \frac{2 \pi}{\omega_n} \]

\[ \text{Underdamped:} \quad \tau_d = \frac{2 \pi}{\omega_d} \]

Comparison of Viscous Damping Cases:

Figure \(\PageIndex{10}\): Responses for all four types of system (or values of damping ratio) in viscous damping. All four systems have the same mass and spring values, and have been given the same initial perturbations (initial position and initial velocity); this is apparent because they start at the same \(y\)-intercept and have the same slope at \(x=0\).

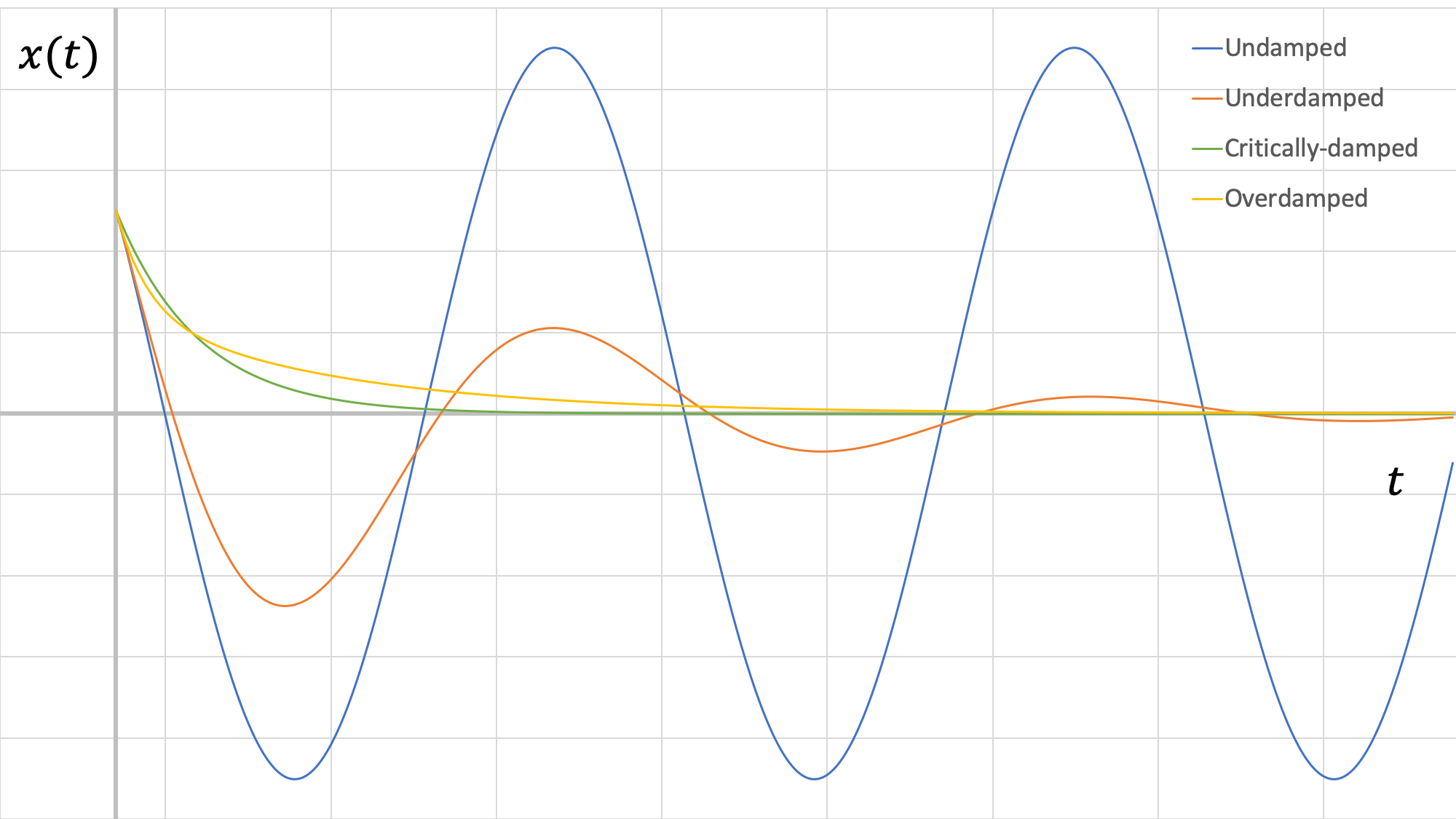
In the figure above, we can see that the critically-damped response results in the system returning to equilibrium the fastest. Also, we can see that the underdamped system amplitude is quite attenuated compared to the undamped case.