15.5: Viscous Damped Harmonic Forced Vibrations

Last updated
Save as PDF

Page ID: 55503

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

As described in the previous section, many vibrations are caused by an external harmonic forcing function (such as rotating unbalance). While we assumed that the natural vibrations of the system eventually damped out somehow, leaving the forced vibrations at steady-state, by explicitly including viscous damping in our model we can evaluate the system through the transient stage when the natural vibrations are present.

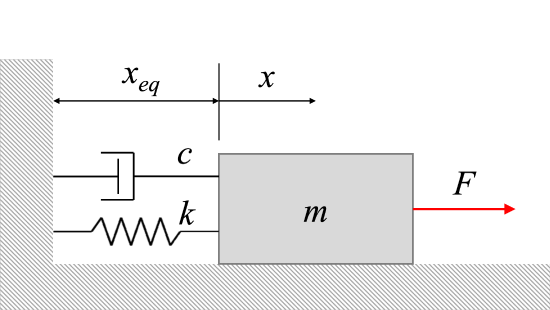
A rectangular mass m is placed on a flat surface. A spring with spring constant k and a viscous linear damper with damping constant c connect the left end of the mass to a vertical wall. The spring is currently at its unstretched length of x_eq. A horizontal pulling force F is applied to the right end of the mass, moving it in the positive x-direction. — Figure \(\PageIndex{1}\): A mass-spring-damper system with an external force, \(F\), applying a harmonic excitation.

Consider the system above. The equation of the system becomes:

\[ m \ddot{x} + c \dot{x} + kx = F_0 \sin (\omega_0 t) \]

\[ \Rightarrow \ddot{x} + \frac{c}{m} \dot{x} + \frac{k}{m} x = \frac{F_0}{m} \ \sin (\omega_0 t). \]

Because the natural vibrations will damp out with friction (as mentioned in undamped harmonic vibrations), we will only consider the particular solution. This particular solution will have the form:

\[ x_p (t) = X' \sin (\omega_0 t - \phi '). \]

After solving, we determine that the expressions for \(X'\) and \(\phi '\) are:

\[ X' = \frac{ \dfrac{F_0}{k}}{ \sqrt{ \left[ 1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2 \right] ^2 + \left[ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} \right] ^2 }} \]

\[ \phi ' = \tan ^{-1} \left[ \frac{ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} }{1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2} \right]. \]

The magnification factor now becomes:

\[ MF = \frac{X'}{\dfrac{F_0}{k}} = \dfrac{1}{\sqrt{ \left[ 1 - \left( \dfrac{\omega_0}{\omega_n} \right) ^2 \right] ^2 + \left[ 2 \dfrac{c}{c_c} \dfrac{\omega_0}{\omega_n} \right] ^2 }} \]

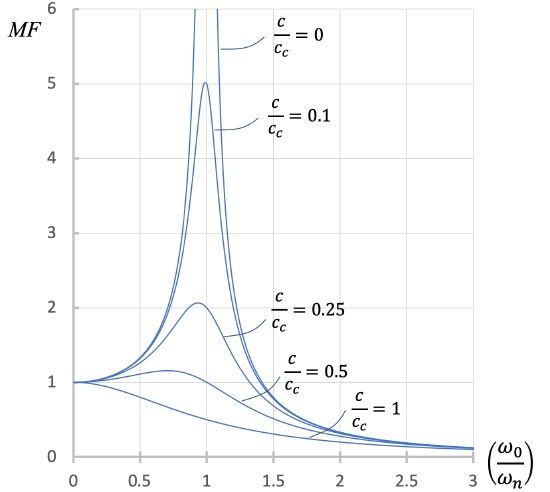
Graph of MF on the vertical axis vs the ratio of initial angular velocity to system angular natural frequency on the horizontal axis, for varying values of the damping ratio. Each graph starts at the point (0,1), reaches a single crest close to x=1, and goes to 0 as the x-axis goes to infinity. The amplitude of that crest is at its minimum when the damping ratio equals 1, and goes to infinity when the damping ratio equals 0. — Figure \(\PageIndex{2}\): This figure shows the various magnification factors associated with different levels of (under)damping.

From the figure above, we can see that the extreme amplitudes at resonance only occur when the damping ratio = 0 and the ratio of frequencies is 1. Otherwise, damping inhibits the out-of-control vibrations that would otherwise be seen at resonance.