16.3: Dot Product

Last updated
Save as PDF

Page ID: 55333

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

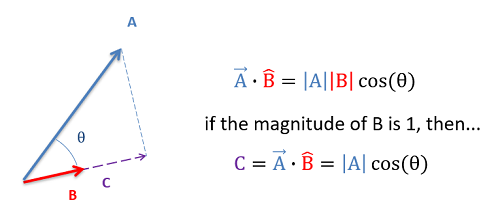
The dot product (also sometimes called the scalar product) is a mathematical operation that can be performed on any two vectors with the same number of elements. The result is a scalar number equal to the magnitude of the first vector, times the magnitude of the second vector, times the cosine of the angle between the two vectors.

\[ \vec{A} \cdot \vec{B} = |A| |B| \cos (\theta) \]

In engineering mechanics, the dot product is used almost exclusively with a second vector being a unit vector. If the second vector in the dot product operation is a unit vector (thus having a magnitude of 1), the dot product will then represent the magnitude of the first vector in the direction of the unit vector. In this respect, a dot product is useful in determining the component of a given vector in any given direction, where the direction is given in terms of a unit vector.

Vector A points sharply upwards and to the right. A shorter vector B originates from the same point that A does, pointing less sharply upwards and to the right. The two vectors create an angle of theta between them. A third vector C, drawn as a dotted line, points along B and extends it to form one leg of a right triangle with vector A as its hypotenuse. C represents the dot product of A and B, which is the product of the lengths of A and B with cos(theta). If B is a unit vector with magnitude 1, the dot product is simply the magnitude of A times cos(theta). — Figure \(\PageIndex{1}\): The dot product of a vector with a unit vector will give you the magnitude of the first vector in the direction of the unit vector.

As an alternative to the above equation for calculating the dot product, we can also calculate the dot product without knowing the angle between the vectors (\(\theta\)). For this method, we break each vector down into components and take the sum of each set of components multiplied together as shown in the equation below.

\[ \vec{A} \cdot \vec{B} = (A_x * B_x) + (A_y * B_y) + (A_z * B_z) \]

Finally, as with many vector operations, the true strength of the dot product is that computers can calculate them very quickly. Both MATLAB and the Wolfram Alpha Vector Operation Calculator are able to compute dot products for you.

Video lecture covering this section, delivered by Dr. Jacob Moore. YouTube source: https://youtu.be/-MMHU4UhutQ.

Example \(\PageIndex{1}\)

Find the dot product of force vector \(\vec{A}\) with the given unit vector \(\hat{B}\).

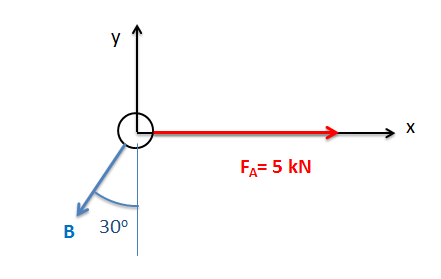
A standard-orientation, two-dimensional Cartesian coordinate plane with two vectors radiating out from the origin. Vector A has a magnitude of 5 kN and points in the positive x-direction. Vector B, a unit vector, points 30° clockwise from the negative y-direction. — Figure \(\PageIndex{2}\): problem diagram for Example \(\PageIndex{1}\). A force vector and a unit vector radiate out from the origin of a two-dimensional Cartesian coordinate system.

Solution:: Video \(\PageIndex{2}\): Worked solution to example problem \(\PageIndex{1}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/JJ3aXtIZwZ0.

Example \(\PageIndex{2}\)

Calculate the dot product of \(\vec{A}\) with \(\vec{B}\) by hand.

Vector A has x, y, z components [1, 3, 5]. Vector B has x, y, z components [6, 4, 2]. Find their dot product. — Figure \(\PageIndex{3}\): problem diagram for Example \(\PageIndex{2}\).

Solution:: Video \(\PageIndex{3}\): Worked solution to example problem \(\PageIndex{2}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/NuuYcDNeja4.

Example \(\PageIndex{3}\)

Calculate the dot product of \(\vec{A}\) with \(\vec{B}\) using MATLAB.

Solution:: Video \(\PageIndex{4}\): Worked solution to example problem \(\PageIndex{3}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/B8PKJtL63C0.

Example \(\PageIndex{4}\)

Calculate the dot product of \(\vec{A}\) with \(\vec{B}\) using the Wolfram Vector Operation Calculator.

Solution:: Video \(\PageIndex{5}\): Worked solution to example problem \(\PageIndex{4}\), provided by Dr. Jacob Moore. YouTube source: https://youtu.be/2FZSXFASFiQ.