1.9: Moderately Large Deflections of Beams and Plates
- Page ID
- 21695
A complete presentation of the theory of moderately large deflections of plates, derived from first principles is presented in the course 2.081 Plates and Shells. The lecture notes for this course are available on OpenCourseWare. There the strain-displacement relation for the theory of moderately large deflection of beams are derived. Here the corresponding equations for plates are only stated with a physical interpretation. An interested reader is referred to the Plates and Shells notes for more details.
Defining moderately large deflections of beams
What are the “moderately large deflections” and how do they differ from the “small deflection”. To see the difference, it is necessary to consider the initial and deformed configuration of the beam axis. The initial and current length element in the undeformed and deformed configuration respectively is denoted dx and ds, as in Figure (\(\PageIndex{1}\))
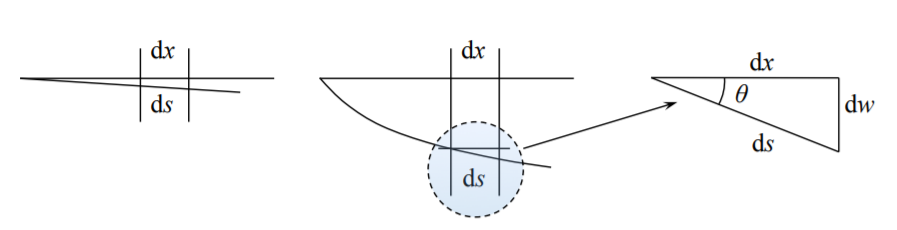
Figure \(\PageIndex{1}\): Change of length of the beam axis produced by rotation.
From the geometry of the problem
\[dx = ds \cos \theta \approx ds \left[1 − \frac{\theta^2}{2}\right] \label{1.9.1}\]
One can distinguish between three theories:
(i) Small deflections, linear geometry \(\theta^2 \ll 1, \; dx \approx ds\), Figure (\(\PageIndex{1}\)(a)).
(ii) Moderately large deflections. The two-term expansion of the cosine function gives a good approximation for \(0 < \theta < 10^{\circ}\). Relation between d\(x\) and d\(s\) is given by Equation \ref{1.9.1}, Figure (\(\PageIndex{1}\)(b)).
(iii) For larger rotation, a full nonlinearity of the problem must be considered.
The present derivation refers to case (ii) above. The Cauchy strain measure, defined in Equation (1.1.3) is adopted:
\[\epsilon = \frac{ds^2-dx^2}{2dx^2}\]
The current length d\(s\) can be expressed in terms of d\(x\) and d\(w\), see Figure (\(\PageIndex{1}\))
\[ds^2 = dx^2 + dw^2\]
From the above two equations, the strain of the beam axis due to element rotation, \(\epsilon_{\text{rot}}\) is
\[\epsilon = \frac{1}{2} \left( \frac{dw}{dx} \right)^2 = \frac{1}{2}\theta^2\]
The beam axis also extends due to the gradient of the axial component of the displacement vector, defined by Equation (1.5.13). Therefore the total strain of the beam axis due to the combined extension and rotation is
\[\epsilon^{\circ} = \frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2 \]
It can be noticed that the second term in the above equation is always positive while the first term can be either positive or negative. In a special case the two terms can cancel one another even though a beam undergoes large deformation.
The question often asked by students is if the expression for the curvature, given by Equation (1.5.14) should also be modified due to larger rotation. From the mathematical point of view the answer is YES. But engineers have a way to get around it.
In the rectangular coordinate system the exact definition of the curvature of the line is:
\[\kappa = \frac{-\frac{d^2w}{dx^2}}{\left( 1+ \left(\frac{dw}{dx}\right)^2\right)^{3/2}} \label{1.9.6}\]
In the limit \(\frac{dw}{dx} \rightarrow 0\) the linear definition is recovered from the nonlinear equation Equation \ref{1.9.6}. The difference between Equation (1.5.14) and Equation \ref{1.9.6} is small in the case of moderately large deflection.
The total strain at an arbitrary point of a beam undergoing moderately large deflection is
\[\epsilon = \underbrace{\frac{du}{dx} + \frac{1}{2} \left( \frac{dw}{dx} \right)^2}_{\text{membrane strain} \; \epsilon^{\circ}} + \underbrace{z\kappa}_{\text{bending strain} \; z\kappa}\]
Extension to Moderately Large Deflection of Plates
In the compact tensorial notation, the nonlinear strain-displacement relation takes the form
\[\epsilon_{\alpha \beta} = \frac{1}{2}(u_{\alpha , \beta} + u_{\beta , \alpha}) + \frac{1}{2} w_{, \alpha} w_{ , \beta} + z\kappa_{\alpha \beta}\]
By comparing with a similar expression for the small deflection theory, Equation (1.7.10) and Equation (1.7.11), the new nonlinear term is
\[\frac{1}{2} w_{, \alpha} w_{ , \beta} = \frac{1}{2} \frac{\partial w}{\partial x_{\alpha}} \frac{\partial w}{\partial x_{\beta}}\]
This term forms a \(2 \times 2\) matrix:
\[\left|\begin{array}{cc}
\frac{1}{2}\left(\frac{\partial w}{\partial x}\right)^{2} & \frac{1}{2} \frac{\partial w}{\partial w} \frac{\partial x}{\partial y} \\
\frac{1}{2} \frac{\partial w}{\partial y} \frac{\partial w}{\partial x} & \frac{1}{2}\left(\frac{\partial w}{\partial y}\right)^{2}
\end{array}\right|=\left|\begin{array}{c}
\frac{\theta_{x}^{2}}{2}, \frac{1}{2} \theta_{x} \theta_{y} \\
\frac{1}{2} \theta_{x} \theta_{y}, \frac{\theta_{y}^{2}}{2}
\end{array}\right|\]
The diagonal terms represent square of the slope of the deflection shape in \(x\) and \(y\) directions. The non-diagonal terms are symmetric and are a product of slopes in the two directions. This term vanishes for cylindrical bending.


